THIẾT KẾ CHUỖI TRẢI TRỰC GIAO SUY RỘNG
CHO HỆ THỐNG QS-CDMA
TRỊNH QUANG KHẢI
Bộ môn Kỹ thuật viễn thông
Khoa Điện – Điện tử
Trường Đại học Giao thông Vận tải
FAN PING ZHI
Viện Thông tin Di động
Trường Đại học Giao thông Tây Nam, Trung Quốc
Tóm tắt: Để giảm thiểu hoặc loại bỏ giao thoa đa truy nhập và giao thoa đa đường trong
các hệ thống CDMA xấp xỉ đồng bộ như LAS-CDMA, yêu cầu đặt ra là phải thiết kế được tập
chuỗi trải trực giao trong một miền dịch pha, hay còn được gọi là miền trực giao. Bài báo này
giới thiệu việc thiết kế các chuỗi trải mới như chuỗi trực giao suy rộng và xấp xỉ trực giao suy
rộng trong các hệ thống QS-CDMA trải phổ trực tiếp. Bên cạnh việc thiết kế, bài báo này
cũng thảo luận và phân tích lý thuyết giới hạn của các chuỗi GO/GQO tuần hoàn và không
tuần hoàn, cùng ứng dụng của các chuỗi đó trong hệ thống QS-CDMA.
Summary: For various quasi-synchronous (QS) CDMA systems such as LAS-CDMA
system emerging recently, to reduce or eliminate the multiple access interference and
multipath interference, it is essential to design a set of spreading sequences, mutually
orthogonal within a designed shift zone, also called orthogonal zone. In this paper, new
concepts of generalized orthogonality (GO) and generalized quasiorthogonality (GQO) for
spreading sequence design in direct sequence (DS) QS-CDMA systems are presented. Besides,
selected GO/GQO sequence design and general theoretical periodic and aperiodic limits,
together with application in QS-CDMA system, are also reviewed and analyzed.
CT 2
I. GIỚI THIỆU
Trong hệ thống CDMA trải phổ trực tiếp (DS-CDMA), tất cả các thuê bao sử dụng cùng
băng tần, nhưng mỗi tín hiệu phát được gán một chuỗi trải riêng. Dạng chuỗi, độ dài và tốc độ
chíp sẽ xác định khả năng của hệ thống.
Các chuỗi Walsh và chuỗi trực giao độ dài biến đổi có thuộc tính trực giao hoàn hảo với độ
trễ thời gian bằng 0, và là các chuỗi lý tưởng cho truyền dẫn hướng thuận (forward link) của hệ
thống CDMA đồng bộ (S-CDMA, synchronous CDMA). Các chuỗi trải trực giao có thể được
sử dụng nếu tất cả các thuê bao của một kênh đảm bảo được đồng bộ trong một khoảng rất ngắn
thời gian của một chip, do mức tương quan chéo giữa các bản dịch khác nhau của các chuỗi trực
giao thông thường là khác 0. Ngoài vấn đề đồng bộ, trong môi trường thông tin di động, truyền
dẫn đa đường cũng tạo ra các tín hiệu với thời gian trễ khác 0, do đó, làm mất đi tính trực giao
giữa các chuỗi Walsh, …
Đối với hệ thống CDMA không đồng bộ (A-CDMA, asynchronous CDMA), không yêu
cầu có sự đồng bộ giữa các chuỗi trải được truyền, độ trễ giữa các chuỗi trải được truyền là bất
kỳ. Do đó, để loại bỏ giao thoa đa truy nhập, cần thiết kế một tập chuỗi trải có hàm tự tương
quan (ACFs-autocorrelation functions) dạng impulse và các mức tương quan chéo (CCFs-
crosscorrelation functions) bằng 0. Thật không may, theo các định lý biên Welch và các lý
thuyết giới hạn khác, về mặt lý thuyết, không thể thiết kế các chuỗi có thuộc tính lý tưởng như
vậy. Do đó, trong hệ thống A-CDMA, chuỗi trải thông thường được thiết kế sao cho có mức tự
tương quan và tương quan chéo thấp, ví dụ như chuỗi Gold, chuỗi Kasami,…
Để giải quyết những khó khăn trên, hai khái niệm mới, các chuỗi trực giao suy rộng (GO-
generalized orthogonality) và xấp xỉ trực giao suy rộng (GQO-generalized quasi-orthogonality),
đã được đề xuất, áp dụng trong hệ thống CDMA xấp xỉ đồng bộ (QS-CDMA, quasi-synchronous
CDMA), có khả năng loại bỏ giao thoa đa truy nhập và giao thoa đa đường. Cần chú ý rằng, các
chuỗi GO còn được gọi là các chuỗi ZCZ (miền tương quan 0), IFW, ZCW, ZCD, hay NHZ khi
áp dụng đối với hệ thống nhảy tần/thời gian, sử dụng hàm tương quan Hamming.
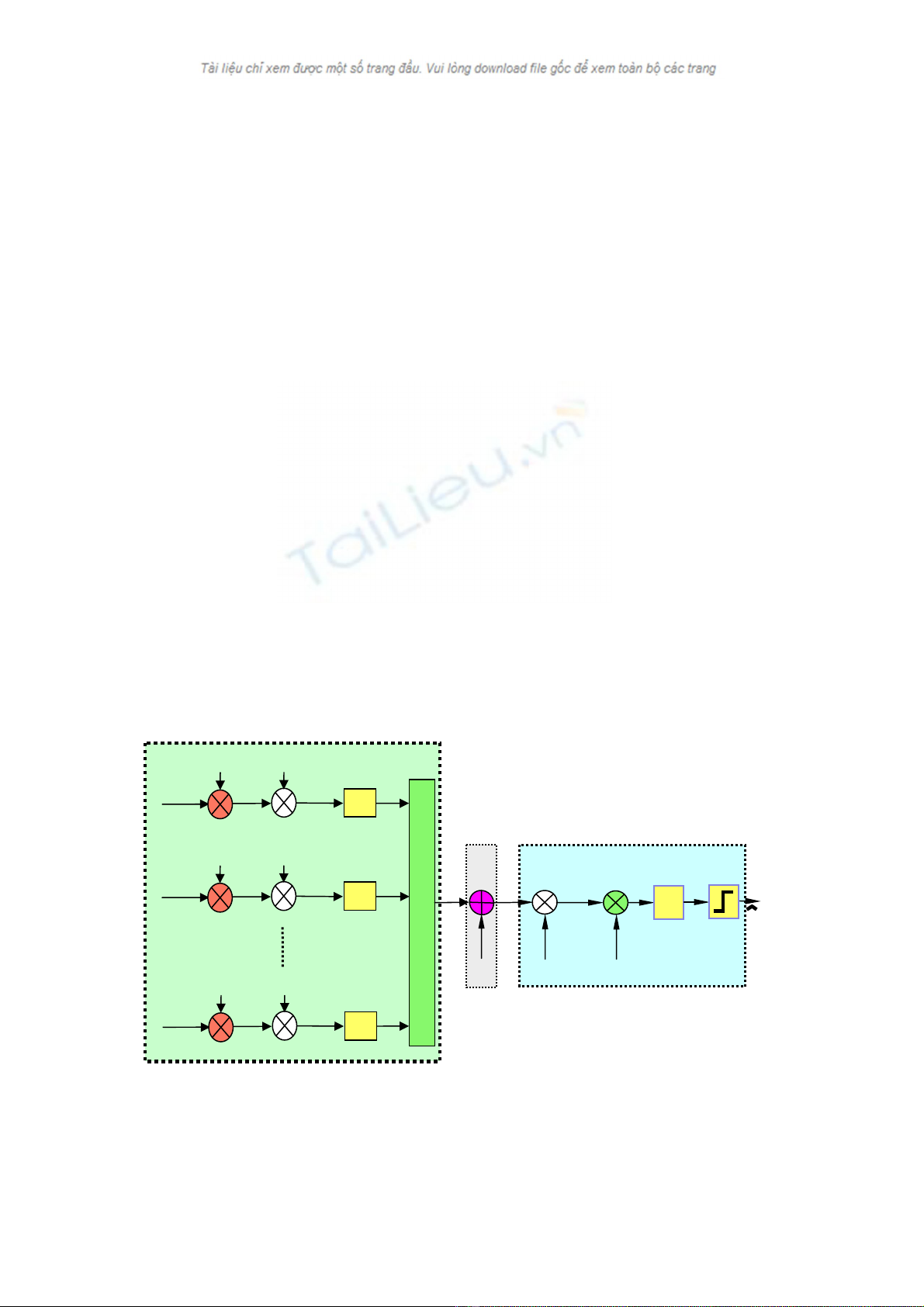
Trong hệ thống QS-CDMA (hình 1), hay còn được gọi là hệ thống CDMA xấp xỉ đồng bộ
(AS-CDMA, approximately synchronous CDMA), các hàm tương quan của các chuỗi trải GO
được đảm bảo nhận giá trị 0 hoặc giá trị rất thấp trong một miền tương quan (miền GO hoặc
GQO) xung quanh gốc thời gian 0. Ý nghĩa của chuỗi GO đối với hệ thống QS-CDMA là dù độ
trễ giữa các tín hiệu trải nhận được do bị ảnh hưởng của truy nhập đồng bộ và truyền dẫn đa
đường thì tính trực giao giữa các tín hiệu vẫn được duy trì miễn là độ trễ không vượt quá giới
hạn cho phép.
Một ví dụ điển hình về hệ thống QS-CDMA có thể kể đến là hệ thống CDMA đồng bộ
vùng rộng (LAS-CDMA, large area synchoronous CDMA), sử dụng các chuỗi trải tam phân (-1,
0, 1) LA (large area ternary sequences) và LS (loosely synchronous), hay các chuỗi mã thông
minh (smart code sequences). Do dung lượng hệ thống và hiệu quả phổ cao, công nghệ LAS-
CDMA trở thành một ứng viên cạnh tranh cho công nghệ 4G.
CT 2
Hình 1. Các mô hình hệ thống CDMA
A
-CDMA:
τ
k bất kỳ
QS-CDMA:
τ
k
≤
Z0
a(1)(t)
s1(t)
Σ
Bộ quyết
định
Kênh Đầu thu
AWGN
b
T
0
∫
τ
1
a(2)(t)
τ
2
a(M)(t) √(2P)cos(
ω
ct+
θ
M
)
b(M)
(t
)
τ
M
b(2)
√(2P)cos(ωt + θ1)
√(2P)cos(ωct + θ2)
Độ trễ
Độ trễ
Độ trễ
s2(t)
sM(t)
S
-CDMA:
τ
k=0
t
b(1)
t
n(t)
r(t)
a(i)(t)
cos(
ω
ct)
Z
(i) b(i)(t)
Đầu phát
Các nội dung tiếp theo của bài báo này được sắp xếp như sau: trong phần 2, định nghĩa các
khái niệm chuỗi mới như trực giao suy rộng, và xấp xỉ trực giao suy rộng, được trình bày kèm
theo ví dụ minh họa. Phần 3 giới thiệu các định lý mới về giới hạn biên của chuỗi. Phương thức
thiết kế chuỗi trực giao suy rộng nhị phân dựa trên cặp chuỗi bù được đề cập trong phần 4. Phần
5 trình bày mô hình hệ thống QS-CDMA sử dụng chuỗi trực giao suy rộng và tính toán BER
trong hệ thống đó.
II. ĐỊNH NGHĨA CHUỖI TRỰC GIAO, TRỰC GIAO SUY RỘNG, XẤP XỈ TRỰC
GIAO VÀ XẤP XỈ TRỰC GIAO SUY RỘNG
Xét một tập hợp chuỗi gồm M chuỗi, mỗi chuỗi có độ dài là N, r = 1, 2, …, M; n = 0,
1, …, (N-1). Tập chuỗi này được gọi là trực giao, hay trực giao suy rộng khi thỏa mãn các tính
chất tương quan tuần hoàn tương ứng dưới đây:
}a{ )r(
n
()
⎩
⎨
⎧
≠=τ
==τ
==τθ ∑
−
=
τ+ ,sr,0for,0
,sr,0for,N
aa
1N
0n
)s(
n
)r(
ns,r (1)
()
⎪
⎩
⎪
⎨
⎧
≤τ<
≠=τ
==τ
==τθ ∑
−
=
τ+
,Z0for,0
,sr,0for,0
,sr,0for,N
aa
0
1N
0n
)s(
n
)r(
ns,r (2)
Ở đó, (n + τ) được tính theo modulo N. Các chuỗi trên được ký hiệu tương ứng là G(N, M)
và GO(N, M, Z0). Dễ thấy, GO(N, M, 0) = G(N, M). Khi r = s các hàm trên đây được gọi là hàm
tự tương quan của chuỗi r (hoặc s), khi r ≠ s gọi là hàm tương quan chéo của chuỗi r và s.
CT 2
Từ công thức 1, có thể nhận thấy, với các chuỗi trực giao thông thường, giá trị tương quan
giữa các chuỗi thứ r và thứ s của tập chuỗi bằng 0 chỉ tại thời điểm độ trễ thời gian bằng 0. Ở
các thời điểm khác, nói chung, giá trị này khác 0, ví dụ như trường hợp của chuỗi Walsh. Đây là
nguyên nhân làm tăng ảnh hưởng của giao thoa đa đường.
Trong công thức 2, giá trị Z0 biểu diễn độ rộng của miền trực giao. Hiển nhiên, với một
chuỗi có độ dài xác định, giá trị này càng lớn càng tốt. Khi Z0 = 0, chuỗi GO trở thành chuỗi
trực giao thông thường.
Để tăng kích thước cuả tập chuỗi nhưng vẫn đảm bảo mức giao thoa giữa các thuê bao
thấp, chuỗi xấp xỉ trực giao QO(N, M, ε) được định nghĩa như dưới đây:
()
⎩
⎨
⎧
≠=τε≤
==τ
==τθ ∑
−
=
τ+ ,sr,0for,
,sr,0for,N
aa
1N
0n
)s(
n
)r(
ns,r (3)
trong công thức 3, giá trị ε rất nhỏ khi so với N.
Từ đó, chuỗi xấp xỉ trực giao suy rộng, GQO(N, M, ε, L0) được định nghĩa như sau:
()
⎪
⎩
⎪
⎨
⎧
≤τ<ε≤
≠=τε≤
==τ
==τθ ∑
−
=
τ+
,L0for,
,sr,0for,
,sr,0for,N
aa
0
1N
0n
)s(
n
)r(
ns,r (4)
Ở đây, L0 được gọi là miền xấp xỉ trực giao suy rộng. Rõ ràng rằng, tập GQO, sẽ trở thành
tập QO khi L0 = 0, tập GO khi ε = 0, và là tập trực giao khi cả L0 = 0 và ε = 0.
Tương tự, chuỗi GQO không tuần hoàn (aperiodic GQO), được định nghĩa như sau:
⎪
⎩
⎪
⎨
⎧
≤τ<ε≤
≠=τε≤
==τ
==τδ ∑τ−−
=
τ+
,L0for,
,sr,0for,
,sr,0for,N
aa)(
0
1N
0n
)s(
n
)r(
ns,r (5)
Mối quan hệ giữa hàm tương quan tuần hoàn, , (hay còn gọi là hàm tương quan chẵn-
even correlation), hàm tương quan lẻ (odd correlation), , với hàm tương quan không tuần
hoàn, , được biểu diễn bởi công thức:
s,r
θ
s,r
ˆ
θ
s,r
δ
(
)
(
)
() ( )
N
ˆ
N
s,rs,rs,r
s,rs,rs,r
−τδ−τδ=θ
−τδ+τδ=θ (6)
Ví dụ 1: Giả sử cho hai chuỗi GO a1, và a2 như dưới đây, các hàm tự tương quan và tương
quan chéo của hai chuỗi a1 và a2 được biểu diễn trong hình 2.
CT 2
Hình 2. Các hàm tự tương quan và tương quan chéo của hai chuỗi GO a1 và a2
a1= [1, -1, -1, -1, 1, -1, -1, -1, -1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1, 1, 1, -1, -1, -1, 1, -1, 1, 1, -
1, 1, -1, -1]
a2= [1, 1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, 1, -1, -1, 1, -1, 1, 1, -1, 1, 1, 1, 1, -1, -1, -
1, -1, 1]
III. CÁC ĐỊNH LÝ VỀ GIỚI HẠN CỦA CHUỖI GO/GQO
Phần dưới đây giới thiệu các định lý về lý thuyết giới hạn mới trong việc thiết kế các chuỗi
GO/GQO tuần hoàn và không tuần hoàn.
a. Đối với chuỗi tuần hoàn
Mối quan hệ giữa hàm tự tương quan θa, tương quan chéo θc, N, M và L0 được xác lập bởi
bất đẳng thức:
()
1LM
N
N
M
1
1
1L
1
1
M
1
0
2
2
c
2
a
0+
−≥θ
⎟
⎠
⎞
⎜
⎝
⎛−+θ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
− (7)
Trong trường hợp L0 = N - 1, bất đẳng thức (7) trên trở thành giới hạn biên Sarwate:
()
1
N
1
N1M
1N 2
c
2
a
2≥θ+θ
−
− (8)
Nếu đặt θm = max{θa, θc}, (8) trở thành giới hạn biên Welch nổi tiếng:
(
)
1MN
N1M 2
2
m−
−
≥θ (9)
Từ (9), có thể nhận thấy rằng, θm chỉ có thể bằng 0 khi và chỉ khi M = 1 và N ≠ 1. Với
chuỗi nhị phân, chỉ có duy nhất một chuỗi có độ dài bằng 4 thỏa mãn θm = 0, là chuỗi
{an} = (1110). Tuy nhiên, từ giới hạn biên GO của Tang-Fan[5] đã chỉ ra, θm có thể nhận giá trị 0
trong toàn bộ miền Z0 thỏa mãn.
CT 2
1
M
N
Z0−≤ (10)
b. Đối với chuỗi không tuần hoàn
Giới hạn biên Peng-Fan xác lập quan hệ giữa hàm tự tương quan δa, tương quan chéo δc, N,
M và L0 như sau:
()( )
222
c
2
aMLML2MNL3N3MN31M1L3L3 −−+−≥δ−++δ (11)
Ở đó 0 ≤ L ≤ L0.
Nếu đặt δm = max{δa, δc}, Tang-Fan đã chỉ ra rằng:
()()
1N21MML
1N2MML
0
0
2
m−−+
+
−
+
≥δ (12)
VI. PHƯƠNG PHÁP TẠO CHUỖI NHỊ PHÂN GO
Để thiết kế các chuỗi GO nhị phân có thể dựa trên tập bù trực giao lẫn nhau, cặp chuỗi bù
hoàn hảo hoặc cặp ma trận Hadamard, trong phần này, chúng tôi sẽ giới thiệu một phương thức