
Học Excel -
Thủ Thuật Excel

Các hàm tài chính trong Excel (phần 2)
Tìm hiểu các hàm tài chính trong Excel (phần 2):
Hàm TBILLEQ()
Tính phần trăm lợi nhuận tương ứng với trái phiếu cho trái phiếu kho bạc.
Cú pháp: = TBILLEQ(settlement, maturity, discount)
Settlement : Ngày kết toán chứng khoán, là một ngày sau ngày phát hành chứng
khoán, khi chứng khoán được giao dịch với người mua.
Maturity : Ngày đáo hạn chứng khoán, là ngày chứng khoán hết hiệu lực.
Discount: Tỷ lệ chiết khấu của chứng khoán (xem hàm DISC)
Lưu ý:
Nên dùng hàm DATE(year, month, day) khi nhập các giá trị ngày tháng.
Settlement là ngày mà chứng khoán được bán ra, maturity là ngày chứng khoán hết
hạn. Ví dụ, giả sử có một trái phiếu có thời hạn 30 năm được phát hành ngày
1/1/2008, và nó có người mua vào 6 tháng sau. Vậy, ngày phát hành (issue date)
trái phiếu sẽ là 1/1/2008,Settlement là ngày 1/7/2008, và Maturity là ngày
1/1/2038, 30 năm sau ngày phát hành.
Settlement, và maturity sẽ được cắt bỏ phần lẻ nếu chúng không phải là số nguyên
Nếu settlement và maturity không là những ngày hợp lệ, TBILLEQ() sẽ trả về giá
trị lỗi #VALUE!
Nếu discount ≤ 0, TBILLEQ() sẽ trả về giá trị lỗi #NUM!
Nếu settlement ≥ maturity, hay nếu maturity lớn hơn một năm sau settlement,
TBILLEQ() sẽ trả về giá trị lỗi #NUM!
Hàm TBILLEQ() sẽ tính toán theo công thức sau đây:

Với: DSM : Số ngày giữa settlement và maturity, được tính theo cơ sở một năm có
360 ngày.
Ví dụ:
Tính phần trăm lợi nhuận tương ứng với trái phiếu cho một trái phiếu kho bạc có
ngày kết toán là 31/3/2008, ngày đáo hạn là 1/6/2008, và có tỷ lệ chiết khấu là
9.14% ?
= TBILLEQ(DATE(2008,3,31), DATE(2008,6,1), 9.14%) = 0.094151 (= 9.42%)
Hàm TBILLPRICE()
Tính giá trị dựa trên đồng mệnh giá $100 cho một trái phiếu kho bạc (dựa trên tỷ lệ
chiết khấu, hay tỷ lệ lợi nhuận của nó)
Hàm này là nghịch đảo của hàm TBILLYIELD()
Cú pháp: = TBILLPRICE(settlement, maturity, discount)
Settlement : Ngày kết toán chứng khoán, là một ngày sau ngày phát hành chứng
khoán, khi chứng khoán được giao dịch với người mua.
Maturity : Ngày đáo hạn chứng khoán, là ngày chứng khoán hết hiệu lực.
Discount: Tỷ lệ chiết khấu (tỷ lệ lợi nhuận) của trái phiếu (xem hàm
TBILLYIELD)
Lưu ý:
Nên dùng hàm DATE(year, month, day) khi nhập các giá trị ngày tháng.
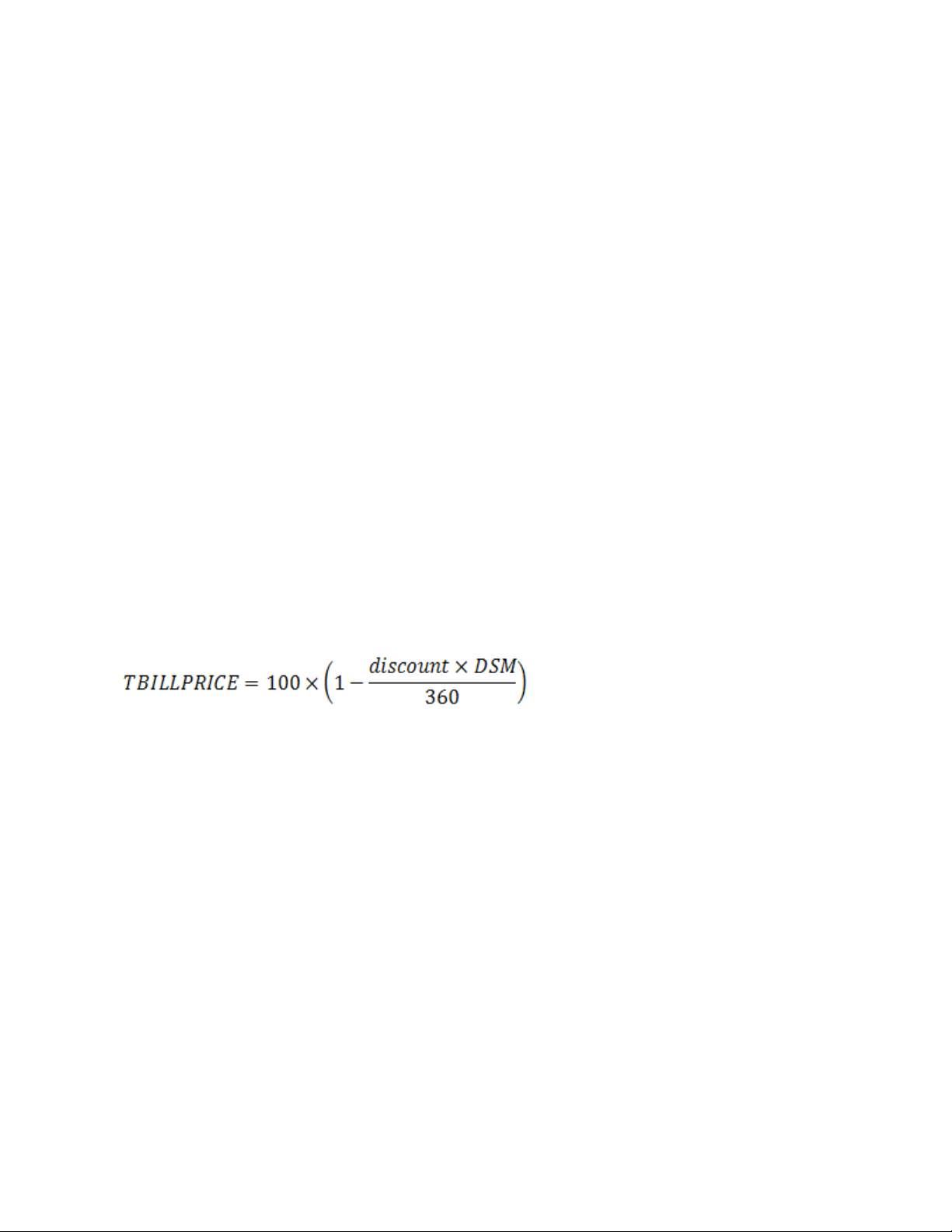
Settlement là ngày mà chứng khoán được bán ra, maturity là ngày chứng khoán hết
hạn. Ví dụ, giả sử có một trái phiếu có thời hạn 30 năm được phát hành ngày
1/1/2008, và nó có người mua vào 6 tháng sau. Vậy, ngày phát hành (issue date)
trái phiếu sẽ là 1/1/2008,Settlement là ngày 1/7/2008, và Maturity là ngày
1/1/2038, 30 năm sau ngày phát hành.
Settlement, và maturity sẽ được cắt bỏ phần lẻ nếu chúng không phải là số nguyên
Nếu settlement và maturity không là những ngày hợp lệ, TBILLPRICE() sẽ trả về
giá trị lỗi #VALUE!
Nếu discount ≤ 0, TBILLPRICE() sẽ trả về giá trị lỗi #NUM!
Nếu settlement > maturity, hay nếu maturity lớn hơn một năm sau settlement (từ
ngày kết toán đến ngày đáo hạn nhiều hơn 1 năm), TBILLPRICE() sẽ trả về giá trị
lỗi #NUM!
Hàm TBILLPRICE() sẽ tính toán theo công thức sau đây:
Với: DSM : Số ngày giữa settlement và maturity, nhưng không tính ngày đáo hạn
(maturity date).
Ví dụ:
Tính giá trị dựa trên đồng mệnh giá $100 cho một trái phiếu kho bạc có ngày kết
toán là 31/3/2008, ngày đáo hạn là 1/6/2008, và có tỷ lệ chiết khấu là 9% ?
= TBILLPRICE(DATE(2008,3,31), DATE(2008,6,1), 9%) = $98.45
Hàm TBILLYIELD()
Tính tỷ lệ chiết khấu (tỷ lệ lợi nhuận) cho một trái phiếu kho bạc (dựa theo giá trị

của đồng $100).
Hàm này là nghịch đảo của hàm TBILLPRICE()
Cú pháp: = TBILLYIELD(settlement, maturity, pr )
Settlement : Ngày kết toán chứng khoán, là một ngày sau ngày phát hành chứng
khoán, khi chứng khoán được giao dịch với người mua.
Maturity : Ngày đáo hạn chứng khoán, là ngày chứng khoán hết hiệu lực.
Pr : Giá trị dựa trên đồng mệnh giá $100 của trái phiếu (xem hàm TBILLPRICE)
Lưu ý:
Nên dùng hàm DATE(year, month, day) khi nhập các giá trị ngày tháng.
Settlement là ngày mà chứng khoán được bán ra, maturity là ngày chứng khoán hết
hạn. Ví dụ, giả sử có một trái phiếu có thời hạn 30 năm được phát hành ngày
1/1/2008, và nó có người mua vào 6 tháng sau. Vậy, ngày phát hành (issue date)
trái phiếu sẽ là 1/1/2008,Settlement là ngày 1/7/2008, và Maturity là ngày
1/1/2038, 30 năm sau ngày phát hành.
Settlement, và maturity sẽ được cắt bỏ phần lẻ nếu chúng không phải là số nguyên
Nếu settlement và maturity không là những ngày hợp lệ, TBILLYIELD() sẽ trả về
giá trị lỗi #VALUE!
Nếu pr ≤ 0, TBILLYIELD() sẽ trả về giá trị lỗi #NUM!
Nếu settlement > maturity, hay nếu maturity lớn hơn một năm sau settlement (từ
ngày kết toán đến ngày đáo hạn nhiều hơn 1 năm), TBILLYIELD() sẽ trả về giá trị
lỗi #NUM!


























