TÍNH TOÁN VÀ MÔ HÌNH HÓA CHO TAY MÁY ROBOT ĐƯỢC
THIẾT KẾ
Thiết lập phương trình động học của tay máy robot
- Bước 1: Gắn hệ toạ độ lên các khâu:
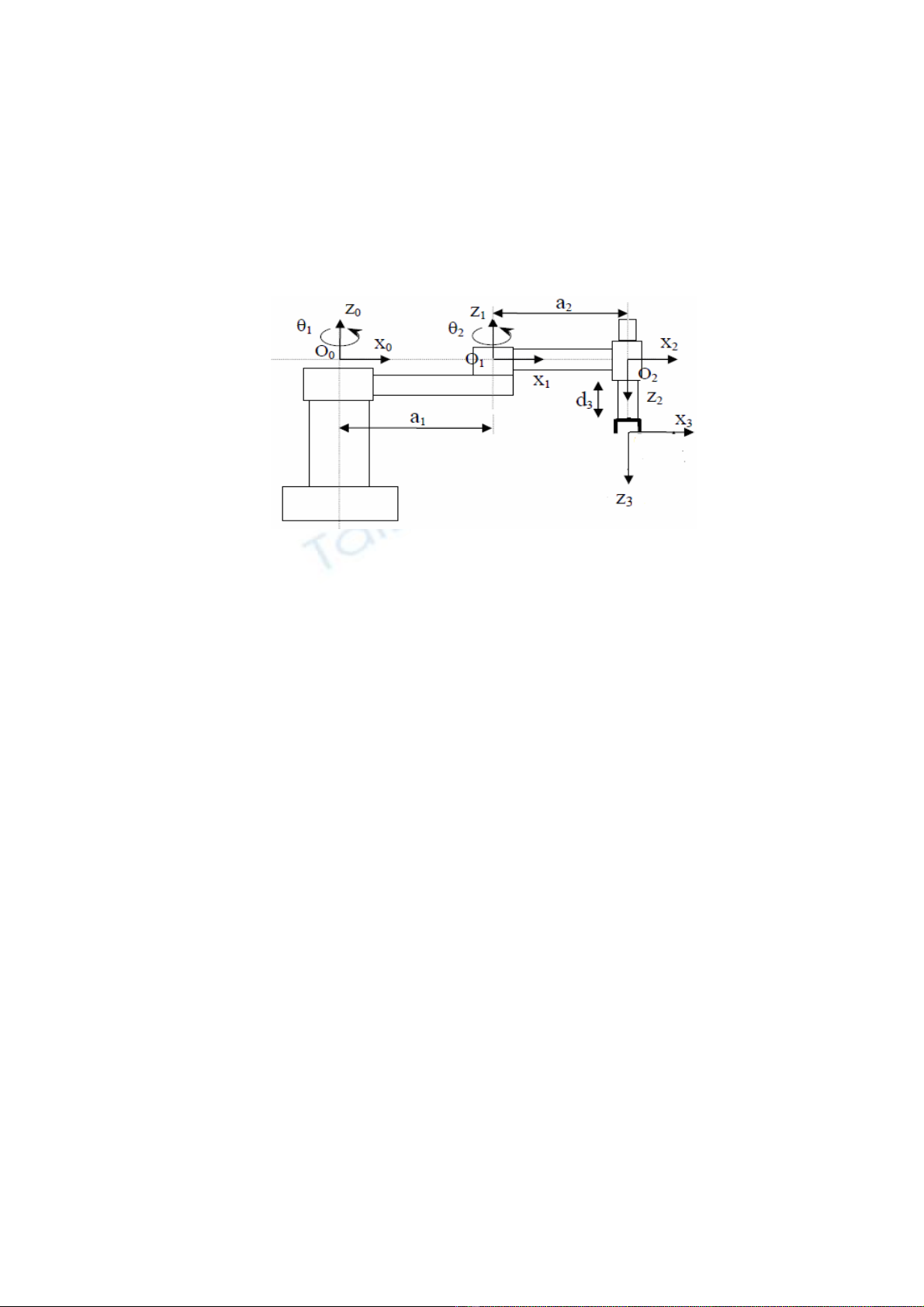
Mô hình cánh tay robot và các hệ trục tọa độ.
Đối với robot loại này các trục khớp đều song song với nhau, các hệ toạ độ đặt tại các
tâm trục khớp. Khâu thứ hai có O2 đặt tại tâm trục khớp ba và z2 hướng về phía các khâu
như hình vẽ.
+ Khâu 1: Có O1 đặt trên trục khớp thứ hai và có x1 hướng từ trục khớp thứ hai đến
trục khớp thứ ba và z1 nằm trên trục khớp thứ hai hướng từ dưới lên trên. Do đó xác định
được O1. Dựa vào quy tắc bàn tay phải ta xác định được y1. Ta thấy z1 song song với z2 nên
O2 tịnh tiến so với O1 trên x1 một đoạn a2 (Trans(a2, 0,0)) và xác định được y2 theo quy tắc
bàn tay phải.
+ Từ O1 ta chon được O0 trên trục khớp một và z0 nằm trên trục khớp một hướng từ
dưới lên trên. O1 chính là O0 tịnh tiến đi một đoạn a1 theo trục x0 (Trans(a1,0,0)) và y0 chọn
theo quy tắc bàn tay phải.
+ Chọn O3: nằm trên tâm của trục khớp ba trùng với trục khớp thứ hai và có z3 cùng
chiều với z2. Do đó O3 chính là O2 tịnh tiến đi một đoạn d3 (Trans(0,0,d3)).
Như vậy, việc gắn hệ toạ độ lên các khâu của robot đã hoàn thành.
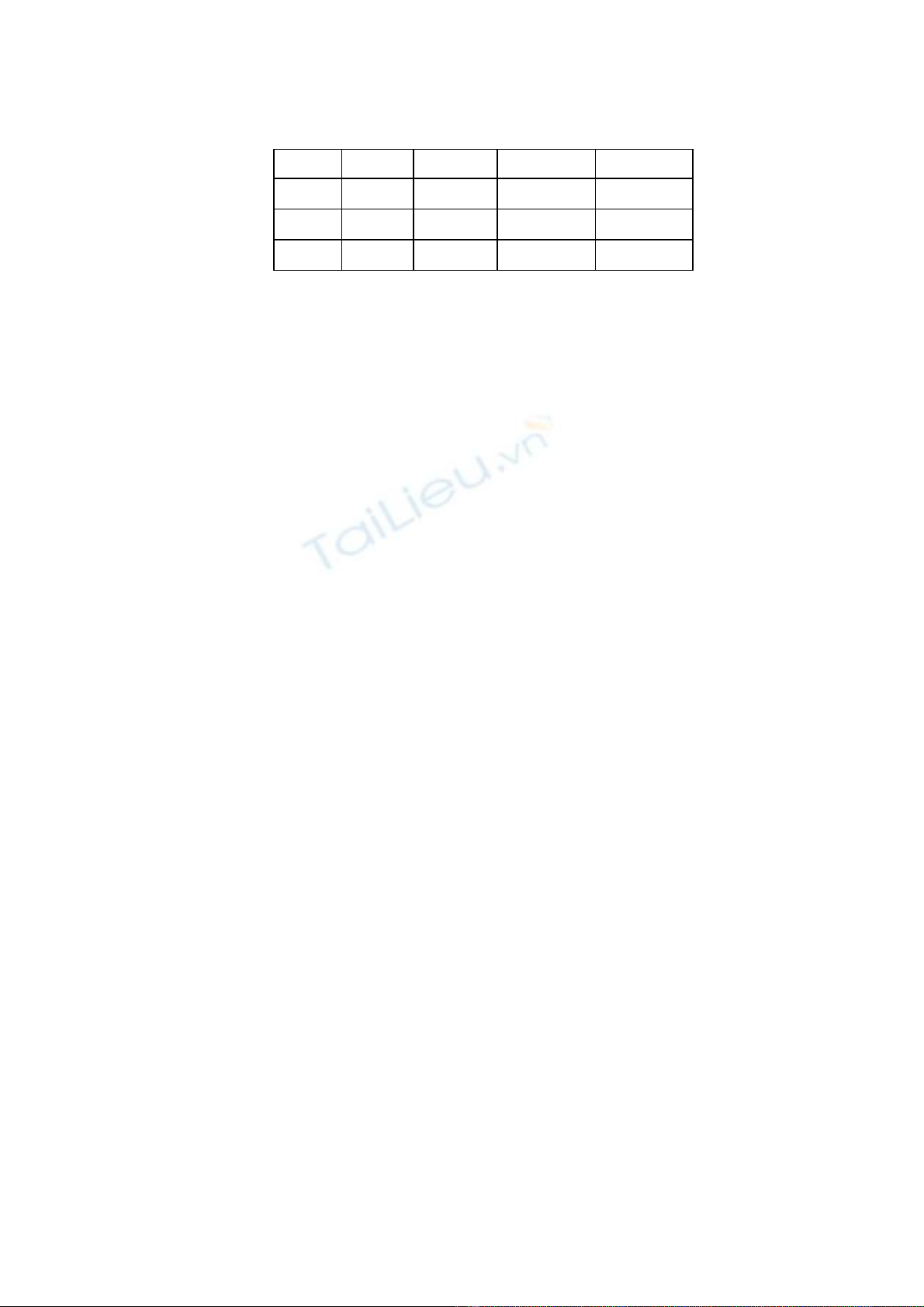
- Bước 2: Lập bảng thông số DH. Thông qua các phân tích trên ta xác định được các
thông số DH của Robot
Khâu
i
i
ai di
1
1
0
a
0
2
2
1800
2
a
0
3 0 0 0 *
3
d
- Bước 3: Xác định các matrận An
Trên cơ sở các hệ toạ độ ấn định cho tất cả các khâu liên kết của Robot ta có thể thiết
lập mối quan hệ giữa các hệ toạ độ nối tiếp nhau (n0); (n-1); (n) bởi các phép quay và tịnh
tiến sau đây:
Quay quanh trục zn-1 một góc n
Tịnh tiến dọc trục zn-1 một đoạn dn
Tịnh tiến dọc trục xn-1 một đoạn an
Quay quanh trục xn một góc xoắn n
Bốn phép biến đổi đồng nhất này thể hiện quan hệ của hệ toạ độ thuộc khâu thứ n so
với hệ toạ độ thuộc khâu thứ n-1 và tích của chúng được gọi là ma trận A.
An = Rot(z,).Trans(0,0,0).Rot(x,)
1000
cossin0
sinsincoscoscossin
cossinsincossincos
d
a
a
An
(4.1)
Ta quy ước: 11 cos
c; 11 sin
s; 22 cos
c; 22 sin
s;
Từ matrận tổng quát An ta xác định được các matrận An của Robot cụ thể như sau:
1000
0100
0
0
1111
1111
1
sacs
casc
A;
1000
0100
0
0
2222
2222
2
sacs
casc
A;
1000
100
0010
0001
3
3d
A
- Bước 4: Tính các ma trận biến đổi thuần nhất
+ Ma trận 33
2AT
+ Ma trận 323
2
23
1.AATAT
+ Ma trận 3213
1
13 .AAATAT
Như vậy:
1000
100
0010
0001
3
3
2
d
T
1000
100
0010
0001
.
1000
0100
0
0
3
2222
2222
3
1
d
sacs
casc
T
1000
100
0
0
3
2222
2222
d
sacs
casc
1000
100
0
0
.
1000
0100
0
0
3
2222
2222
1111
1111
3d
sacs
casc
sacs
casc
T
1000
100
0
0
3
1121221221212121
1121221221212121
3d
sascacsaccsssccs
cascaccacsscsscc
T
Ma trận T3 là ma trận xác định hướng và vị trí của khâu chấp hành cuối
3
1
13
1000
TA
paon
paon
paon
T
zzzz
yyyy
xxxx
(4.2)
Ta có hệ phương trình động học thuận của robot như sau:
0
2121
2121
z
y
x
n
ssccn
scccn
;
0
2121
2121
z
y
x
o
ccsso
cssco
;
1
0
0
z
y
x
a
a
a
;
3
11212212
11212212
dp
sascacsap
cascaccap
z
y
x