ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Saturday, August 06, 2011
Toán cao cp A3 Đi hc 1
TO
TOÁ
ÁN CAO C
N CAO C
P A3
P A3 Đ
Đ
I H
I H
C
C
PHÂN PH
PHÂN PH
I CHƯƠNG TRÌNH
I CHƯƠNG TRÌNH
S
S
ti
ti
t
t: 45
: 45
-----
-----
Chương 1. Hàm số nhiều biến số
Chương 2. Tích phân bội
Chương 3. Tích phân đường – Tích phân mặt
Chương 4. Phương trình vi phân
Tài liệu tham khảo
1. Nguyễn Phú Vinh – Giáo trình Toán cao cấp A3
–
ĐHCN TP. HCM.
2. Đỗ Công Khanh – Giải tích hàm nhiều biến
(tập 3, 4) – NXB
ĐHQG TP. HCM.
Biên
Biên so
so
n
n:
:ThS
ThS.
. Đo
Đoà
àn
nVương
Vương Nguyên
Nguyên
Download Slide
Download Slide b
bà
ài
igi
gi
ng
ng To
Toá
án
nA3
A3 t
t
i
i
dvntailieu.wordpress.com
dvntailieu.wordpress.com
3. Nguyễn Đình Trí – Phép tính Giải tích
hàm nhiều biến – NXB Giáo dục
.
4. Phan Quốc Khánh – Phép tính Vi tích phân (tập 2)
–
NXB Giáo dục.
5. Đặng Văn Vinh – Slide bài giảng Toán A 3
– ĐH Bách khoa Tp.HCM
.
6. Nguyễn Thừa Hợp – Giải tích (tập 1, 2)
– NXB
ĐHQG Hà Nội.
7. Nguyễn Thủy Thanh – Bài tập Giải tích (tập 2)
– NX
B Giáo dục.
8. James Stewart – Calculus Early Transcendentals,
sixth edition
–
USA
2008
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
§1. KHÁI NIỆM CƠ BẢN
1.1.
Các định nghĩa
a) Miền phẳng
• Trong mặt phẳng

, hình phẳng
giới hạn bởi các
đường cong kín được gọi là miền phẳng
. Tập hợp các
đường cong kín giới hạn
được gọi là biên của
, ký
hiệu
∂
hay
Γ
. Đặc biệt, mặt phẳng

được xem là
miền phẳng với biên ở
vô cùng
…………………………………………………………..
§1. Khái niệm cơ bản
§2. Đạo hàm riêng – Vi phân
§3. Cực trị của hàm hai biến số
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Miền phẳng
kể cả biên
∂
được gọi là miền đóng
,
miền phẳng
không kể biên
∂
là miền mở.
• Miền phẳng
được gọi là miền liên thông
nếu có 1
đường cong nằm trong
nối 2 điểm bất kỳ thuộc
.
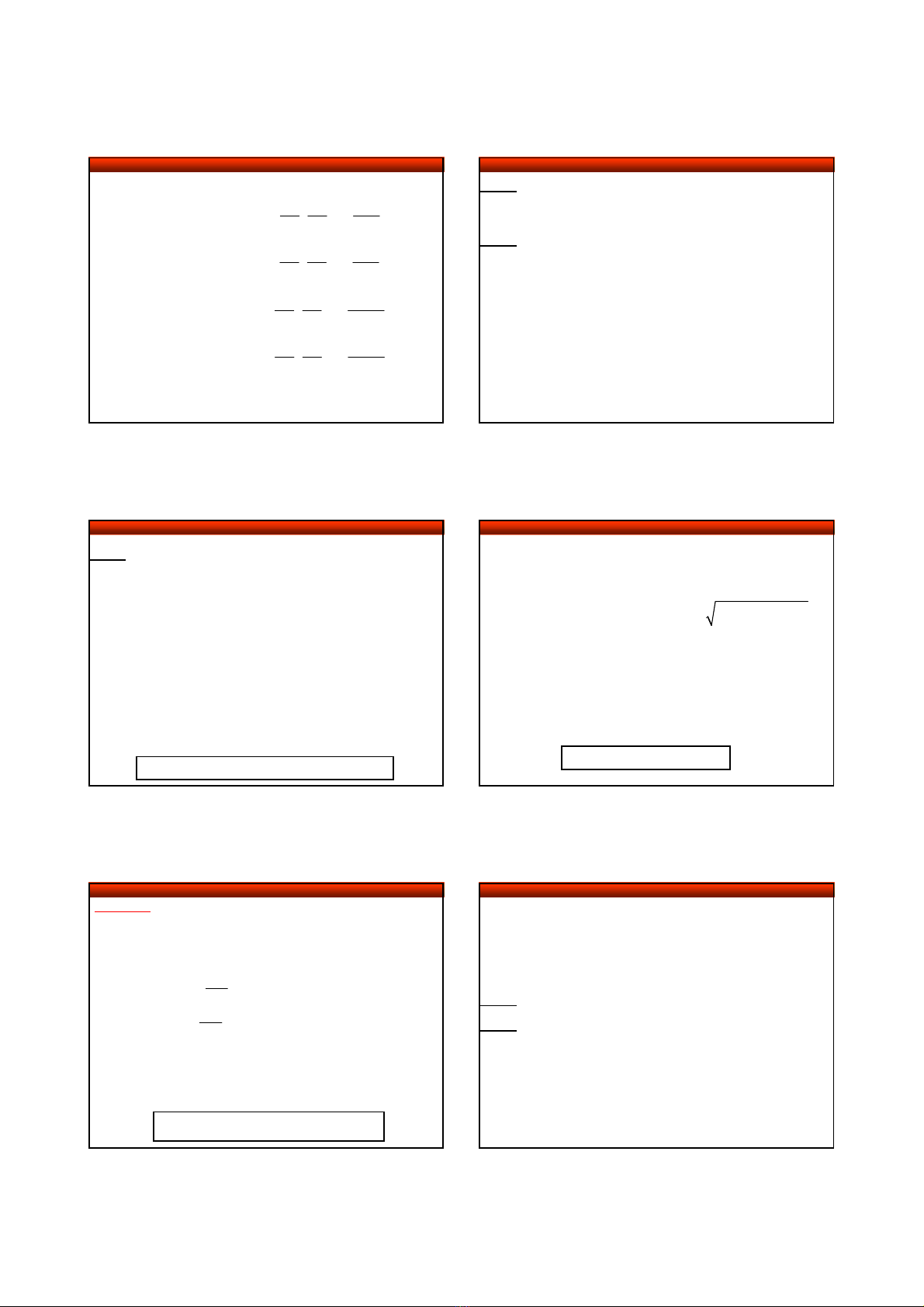
Miền liên thông
có biên là 1 đường cong kín được gọi
là miền đơn liên (hình a)
; có biên là nhiều đường cong
kín rời nhau là
miền đa liên
(hình b).
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
b) Lân cận của một điểm
• Khoảng cách giữa 2 điểm
,
là:
(
)
(
)
(
)
= = − + −
.
• Hình tròn
ε
mở có tâm
, bán kính
ε >
được
gọi là một lân cận của điểm
.
Nghĩa là:
∈ ε ⇔ − + − < ε
.
ε
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Chú ý
• Trong trường hợp xét hàm số
mà không nói gì
thêm thì ta hiểu MXĐ của hàm số là tập tất cả các điểm
∈
ℝ
sao cho
có nghĩa.
c) Hàm số hai biến số
• Trong mặt phẳng

cho tập
⊂
ℝ
.
Tương ứng
→
ℝ
cho tương ứng mỗi
∈
với một giá trị
= ∈
ℝ
duy nhất
được gọi là
hàm số hai biến số
.
• Tập
⊂
ℝ
được gọi là miền xác định (MXĐ)
của hàm
số
, ký hiệu là
. Miền giá trị của hàm
là:
{
}
= = ∈ ∈ℝ
.
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Saturday, August 06, 2011
Toán cao cp A3 Đi hc 2
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Hàm có nhiều hơn hai biến được định nghĩa tương tự.
VD 1.
• Hàm số


= −
có
=
ℝ
.
• Hàm số
= − −
có MXĐ là hình tròn đ
óng
tâm
 
, bán kính
=
.
• Hàm số

= − −
có MXĐ là hình tròn mở
tâm
 
, bán kính
=
.
• Hàm số

= = + −
có MXĐ là nửa
mp mở có biên
+ − =
, không chứa
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
1.2. Giới hạn của hàm số hai biến số
a) Điểm tụ
• Trong mp

cho dãy điểm

=
Điểm
được gọi là điểm tụ
của dãy trên nếu
mọi lân cận của
đều chứa vô số phần tử của dãy.
• Điểm
được gọi là điểm tụ của tập
⊂
ℝ
nếu mọi lân cận của điểm
đều chứa
vô số điểm
thuộc
b) Định nghĩa giới hạn (giới hạn bội)
• Điểm
được gọi là giới hạn của dãy điểm
 
=
nếu
là điểm tụ
duy
nhất của dãy.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Hàm số
có giới hạn là
∈ ±∞
ℝ ∪
khi
dần đến
nếu

→∞
=
. Ký hiệu:
  
→ → →
→
= = =
VD 2.



→ −
− −
= −
+
.
VD 3. Tìm


→
, với

=
+
.
Ký hiệu là:

→∞
=
hay
→∞
→
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Vậy


→
=
.
Nhận xét
• Nếu đặt
 
= + ϕ = + ϕ
thì:
→ ⇔ →
.
VD 4. Tìm



→
+
+
.
Giải.
 
→
→
≤ = ≤ = →
+
.
Giải. Đặt
 
= ϕ = ϕ
, ta có:
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 5. Cho hàm số

=
+
.
Chứng tỏ rằng


→
không tồn tại.
Giải. Đặt
 
= ϕ = ϕ
, ta có:


  
→ →
ϕ
= = ϕ
Do giới hạn phụ thuộc vào
ϕ
nên không duy nhất.
Vậy


→
không tồn tại.

 
 
→ →
+
= =
+
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
c) Giới hạn lặp
• Giới hạn theo từng biến khi
dần đến
của hàm số
được gọi là giới hạn lặp.
Khi
→
trước,
→
sau thì ta viết:
 
→ →
.
Khi
→
trước,
→
sau thì ta viết:
 
→ →
.
VD 6. Xét hàm số
 
−
=
+
. Ta có:

  
→ → →
−
= = −
,
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Saturday, August 06, 2011
Toán cao cp A3 Đi hc 3
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Định lý
Trong
ℝ
cho hình vuông
có 1 đỉnh là
và hàm số
xác định trong
.
Nếu tồn tại

→
= ∈
ℝ
và mỗi
∈
tồn tại

→
ϕ = ∈
ℝ
thì:
  
→ → →
= ϕ =
.

  
→ → →
= =
.
Vậy
   
→ → → →
≠
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Nhận xét
• Nếu
   
→ → → →
≠
thì không tồn
tại

→
.
• Sự tồn tại giới hạn lặp không kéo theo sự tồn tại giới
hạn bội và ngược lại.
1.3. Hàm số liên tục
• Hàm số
liên tục tại
∈ ⊂
ℝ
nếu
 
→
=
• Hàm số
liên tục trên tập
⊂
ℝ
nếu
nó liên tục
tại mọi điểm thuộc
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 7. Xét sự liên tục của
 
−
=
+
.
Giải. Với
 
≠
thì hàm số
xác định nên
liên tục.
Tại
 
thì


→
không tồn tại (VD 6).
Vậy hàm số
liên tục trên
 
ℝ
.
Chú ý
Hàm số
liên tục trên miền đóng giới nội
thì
nó
đạt giá trị lớn nhất
(
max
)
và nhỏ nhất
(
min
)
tr
ên
……………………………………………………………
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
§2. ĐẠO HÀM RIÊNG – VI PHÂN
2.1. Đạo hàm riêng
a) Đạo hàm riêng cấp 1
• Cho hàm số
xác định trên miền mở
⊂
ℝ
chứa điểm
. Cố định
, nếu hàm số
có đạo hàm tại
thì ta gọi đạo hàm đó là
đạo hàm riêng
theo biến
của hàm số
tại
.
Ký hiệu:
hay
hay

∂
∂
Vậy

→
−
=
−
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
• Tương tự, đạo hàm riêng theo biến
tại
là:

→
−
=
−
Chú ý
• Nếu
là hàm số một biến
thì


∂
= =
∂
.
•
Hàm số nhiều hơn hai biến có định nghĩa t
ương tự
VD 1. Tính các đạo hàm riêng của hàm số:

= − + −
tại

−
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 3. Tính các đạo hàm riêng của

=
tại

π
.
VD 4. Tính các đạo hàm riêng của

=
.
b) Đạo hàm riêng cấp cao
• Đạo hàm riêng (nếu có) của hàm số
,
được gọi là các đạo hàm riêng cấp hai của
.
VD 2. Tính các đạo hàm riêng của

+
=
+ +
.
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Saturday, August 06, 2011
Toán cao cp A3 Đi hc 4
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Ký hiệu:
( )


∂ ∂ ∂
= = = =
∂ ∂
∂
,
(
)


∂ ∂ ∂
= = = =
∂ ∂
∂
,
( )

 
∂ ∂ ∂
= = = =
∂ ∂ ∂ ∂
,
(
)

 
∂ ∂ ∂
= = = =
∂ ∂ ∂ ∂
.
•
Hàm số nhiều hơn 2 biến và đạo hàm riêng cấp cao hơn
2 có định nghĩa t
ương tự
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 6. Cho hàm số
= + −
.
Giá trị của đạo hàm riêng cấp năm

−
là:
A.


− =
; B.


− = −
;
C.


− =
; D.


− = −
.
VD 5. Tính các đạo hàm riêng cấp hai của hàm số:
= + −
tại

−
.
• Định lý Schwarz
Nếu hàm số
có các đạo hàm riêng
 
 
liên
tục trong miền mở
⊂
ℝ
thì
 
 
=
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
VD 7. Đạo hàm riêng

−
+
≥
của
−
=
là:
A.
+ −
−
; B.
+ −
−
;
C.
−
−
; D.
−
−
.
2.2. Vi phân
2.2.1. Vi phân cấp 1
a) Số gia của hàm số
• Cho hàm số
xác định trong lân cận
ε
của điểm
. Cho
một số gia
và
một
số gia
, khi đó hàm
có tương ứng số gia:

= + + −
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
b) Định nghĩa
• Nếu trong lân cận
ε
với số gia
,
mà số
gia
tương ứng có thể viết được dưới dạng:
(
)
= + + = +
,
trong đó
là những số
chỉ phụ thuộc vào điểm
và hàm
, không phụ thuộc
thì đại lượng
+
được gọi là vi phân
của
hàm số
tại điểm
.
• Khi đó,
được gọi là khả vi tại điểm
.
Ký hiệu là:

= +
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Nhận xét
• Xét những điểm
+ +
dịch chuyển
trên đường đi qua
song song
. Khi đó
=
:
= + − = +

→
⇒ = ⇒ =
.
Tương tự,

→
= ⇒ =
.
Suy ra
= +
.
• Xét
 
= ⇒ = ⇒ =
.
Tương tự,

=
. Vậy:
  
= +
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
c) Định lý
• Nếu hàm số
có các đạo hàm riêng
trong lân cận
nào đó của
và các đạo hàm riêng này
liên tục
tại
thì
khả vi tại
.
VD 8. Cho hàm
−
= −
. Tính

−
.
VD 9. Tính vi phân cấp 1 của hàm


−
=
.
2.2.2. VI PHÂN CẤP CAO
a) Vi phân cấp 2
• Giả sử
là hàm khả vi với
là các biến độc
lập. Các số gia
 
= =
tùy ý độc
lập với
nên được xem là hằng số đối với
.
ĐH Công nghip Tp.HCM
dvntailieu.wordpress.com
Saturday, August 06, 2011
Toán cao cp A3 Đi hc 5
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Chú ý
• Nếu
là các biến không độc lập (biến trung gian)
= ϕ ψ
,
= ϕ ψ
thì công
thức trên không còn
đúng nữa. Sau đây ta chỉ xét trường hợp
độc lập.
• Vi phân của

được gọi là vi phân cấp 2 của
. Ký hiệu và công thức:
(
)

  
′′ ′′ ′′
= = + +
VD 10. Cho hàm số

= + −
.
Tính vi phân cấp hai


−
.
VD 11. Tính vi phân cấp 2 của hàm


=
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
b) Vi phân cấp n
(
)
 
−
− −
=
= =
∑
Trong đó
=
,
=
,
  
=
,
  
=
.
VD 12. Tính vi phân cấp 3 của hàm số
=
.
VD 13. Tính vi phân
của hàm số

=
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
2.3. Đạo hàm của hàm số hợp
a) Hàm hợp với một biến độc lập
• Cho
là hàm khả vi đối với
và
là những
hàm khả vi đối với biến độc lập
.
Khi đó, hàm hợp của
biến
là
 
ω =
khả vi. Ta có:
 
 
′
ω = +
VD 14. Tính
′
ω
với hàm số
=
và

= − =
.
Giải.
 
 
′
ω = +
   
 
= − + = − +
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Tính trực tiếp như sau:
 
ω = −
    
′
⇒ ω = − − + −


= − +
.
VD 15. Cho
  
= + =
. Tính


.
Gi
ả
i
  


= + + +
 
+
= + =
+ + +
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
b) Hàm hợp với hai biến độc lập
• Cho
là hàm khả vi đối với
và
là những
hàm khả vi đối với hai biến độc lập
ϕ ψ
.
Khi đó, hàm
hợp của 2 biến
ϕ ψ
là
 
ω ϕ ψ = ϕ ψ ϕ ψ
khả vi. Ta có:
ϕ ϕ ϕ ψ ψ ψ
ω = + ω = +
2.4. Đạo hàm của hàm số ẩn (hai biến)
• Hàm
xác định trên
⊂
ℝ
thỏa
phương trình

= ∀ ∈ ⊂
(*) được gọi là
hàm số ẩn
hai biến xác định bởi (*)
.
Chương
Chương 1.
1. H
Hà
àm
ms
s
nhi
nhi
u
ubi
bi
n
ns
s
Giả sử các hàm trên đều khả vi, đạo hàm 2 vế (*) ta được:
+ = + =
.
Vậy
( )
= − = − ≠
VD 16. Cho hàm ẩn
thỏa phương trình:


= + +
. Tính
.
VD 17. Cho hàm ẩn
thỏa phương trình mặt cầu:
+ + − + − − =
. Tính
.