
Lê Thanh Hà, TS.Lê Thanh Hà, TS.
Phòng thí nghiệm Tương tác người máyPhòng thí nghiệm Tương tác người máy

Số lượng dữ liệu âm thành, phim ảnh trở Số lượng dữ liệu âm thành, phim ảnh trở
nên khổng lồ.nên khổng lồ.
Nhưng hệ thống lưu trữ và truyền tải hạn Nhưng hệ thống lưu trữ và truyền tải hạn
chế.chế.
Cần những phương pháp giảm kích thước Cần những phương pháp giảm kích thước
âm thanh và hình ảnh để lưu trữ và truyền âm thanh và hình ảnh để lưu trữ và truyền
tải hiệu quả.tải hiệu quả.
11/4/2013 Lê Thanh Hà 2
11/4/2013 Lê Thanh Hà 3
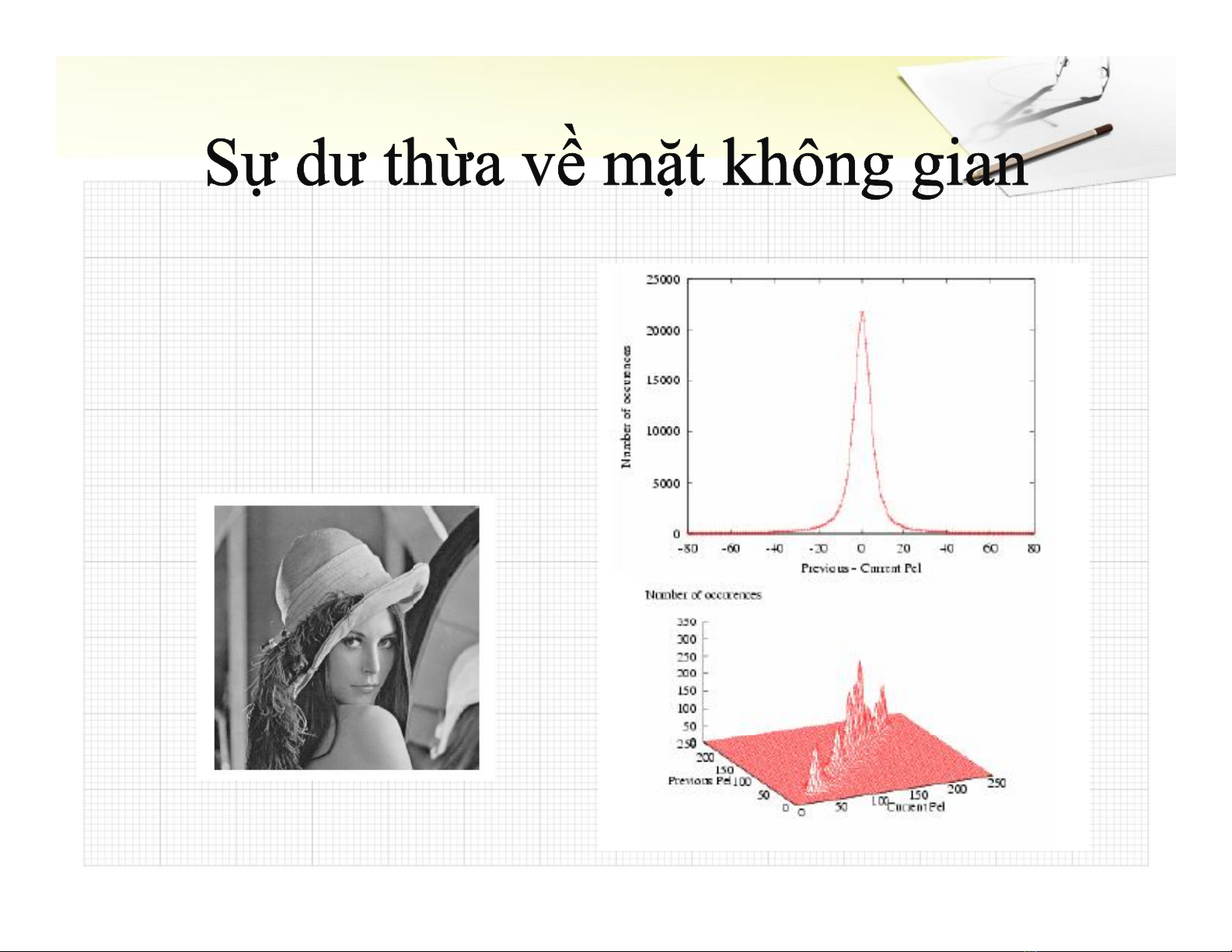
Sự dư thừa về mặt không Sự dư thừa về mặt không
gian chính là ở giữa các gian chính là ở giữa các
điểm của một ảnh. Nói rõ điểm của một ảnh. Nói rõ
hơn, các điểm ảnh hơn, các điểm ảnh
thường có quan hệ mật thường có quan hệ mật
thiết với nhau.thiết với nhau.

11/4/2013 Lê Thanh Hà 4
Mã hóa Entropy (Lossless coding)Mã hóa Entropy (Lossless coding)
Là các dạng mã hóa nhằm loại bỏ các dư thừa thông tin.Là các dạng mã hóa nhằm loại bỏ các dư thừa thông tin.
Thông tin sau khi giải mã bằng chính xác thông tin trước Thông tin sau khi giải mã bằng chính xác thông tin trước
khi mã.khi mã.
Mã hóa dự đoán (Lossy coding)Mã hóa dự đoán (Lossy coding)
Là các dạng mã hóa nhằm loại bỏ các dư thừa thông tin.Là các dạng mã hóa nhằm loại bỏ các dư thừa thông tin.
Thông tin sau khi giải có thể (ít nhiều) khác thông tin trước Thông tin sau khi giải có thể (ít nhiều) khác thông tin trước
khi mã.khi mã.

11/4/2013 Lê Thanh Hà 5
Đo thông tinĐo thông tin
Giả thiết một biểu tượng Giả thiết một biểu tượng x x với xác suất xuất hiện với xác suất xuất hiện pp, ,
thì nội dung thông tin của nó (thông tin chứa trong thì nội dung thông tin của nó (thông tin chứa trong
biểu tượng) là:biểu tượng) là:
Độ đo thông tin không phụ thuộc vào giá trị biểu Độ đo thông tin không phụ thuộc vào giá trị biểu
tượngtượng
Độ đo thông tin chỉ phụ thuộc vào xác suất của biểu Độ đo thông tin chỉ phụ thuộc vào xác suất của biểu
tượngtượng
Khi cơ sở của hàm log là 2 thì đơn vị tính của độ đo Khi cơ sở của hàm log là 2 thì đơn vị tính của độ đo
thông tin gọi là bit.thông tin gọi là bit.
( ) log( ( ))
I x p x


























