11 sai lầm khi tính tích phân

Chia sẻ: Megabookchuyengiasachluyenthi Megabookchuyengiasachluyenthi | Ngày: | Loại File: PDF | Số trang:6

Thêm vào BST

Báo xấu

57
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Mời các bạn cùng tham khảo nội dung tài liệu "11 sai lầm khi tính tích phân" dưới đây để nắm bắt được những sai lầm tính tích phân khi làm Toán, tài liệu hướng dẫn cụ thể chi tiết qua 11 bài tập cụ thể, hy vọng đây là tài liệu tham khảo hữu ích cho các bạn.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: 11 sai lầm khi tính tích phân

11 SAI LẦM KHI TÍNH TÍCH PHÂN 4 Bài 1. Tính tích phân I 1 x2 dx . 0 Lời giải sai: Đặt x sin t dx cos tdt . 4 4 4 1 cos 2t 1 I 1 sin 2 t .cos tdx cos 2 tdt . 0 0 0 2 8 4 Lý do sai: Đổi biến số nhưng không đổi cận. x t ar c sin Lời giải đúng: x sin t dx cos tdt . Khi 4 4. x 0 t 0 arcsin arcsin arcsin 4 4 4 1 cos 2t I 1 sin 2 t .cos tdx cos 2 tdt 0 0 0 2 1 1 arcsin sin 2arcsin . 2 4 4 4 1 dx Bài 2. Tính tích phân I 5 . 0 2x 1 x 1 t 3 Lời giải sai: Đặt t 2x 1 . Khi . x 0 t 1 3 3 dt t4 1 1 20 I 1 . 1 t5 4 1 4 34 81 Lý do sai: Đổi biến không tính vi phân. x 1 t 3 Lời giải đúng: Đặt t 2x 1 dt 2dx . . x 0 t 1 3 3 4 dt t 1 1 10 I 1 . 1 2t 5 8 1 8 34 81 2 Bài 3. Tính tích phân I xe x dx . 0 11 Sai Lầm Khi Tính Tích Phân 3 http://megabook.vn/
u x u' 1 Lời giải sai: Đặt x . v' e v ex 2 2 I xe x e x dx e2 1. 0 0 Lý do sai: Hiểu sai bản chất công thức từng phần. u x du dx Lời giải đúng: Đặt x x . dv e dx v e 2 2 I xe x e x dx e2 1. 0 0 2 Bài 4. Cho n N ; chứng minh I sin sin x nx dx 0. 0 Lời giải sai: Xét hàm số f x sin x sin x nx trên 0; 2 . Ta có f x là hàm liên tục trên 0; 2 và f x sin sin x nx f x . Vậy f x là hàm lẻ, suy ra I 0. Lý do sai: Học sinh hiểu sai về định lý “Nếu hàm số f x là hàm lẻ, liên tục trên a a; a thì f x dx 0 ”. a Lời giải đúng: Đặt x y dx dy . 2 I sin sin x nx dx sin sin y ny n dy 0 n 1 sin ny sin y dy . Mặt khác ta có: g y sin ny sin y xác định trên ; là hàm liên tục và g y sin ny sin y sin ny sin y g y . Suy ra g y là hàm lẻ. Vậy I 0. Bài 5. Cho hàm số f liên tục trên 0; ; hãy so sánh I xf sin x dx và 0 11 Sai Lầm Khi Tính Tích Phân 4 http://megabook.vn/
J f sin x dx . 0 u x du dx Lời giải sai: Đặt . dv f sin x dx v f cos x I xf cos x f cos x dx . 0 0 Do f liên tục trên 0; , suy ra f cos f 0 0 I f cos x dx (1). 0 Mà J f sin x dx (2). 2 0 Từ (1) và (2) ta có I J. Lý do sai: Học sinh không hiểu về hàm liên tục, tích phân và vi phân. Lời giải đúng: Đặt x t dx dt . 0 I t f sin t dt f sin x dx xf sin x dx 0 0 2I f sin x dx I f sin x dx . 0 2 0 Vậy ta có I J. Bài 6. Cho hàm số f liên tục trên a; b ; chứng minh tồn tại ít nhất một điểm c b C a; b sao cho f x f c dx f c f x dx . a c Lời giải sai: Do f liên tục trên a; b , suy ra f x f c trên a , c bằng f x f c trên b , c , vậy ta có c b c f x f c dx f x f c dx f c f x dx . b a c Lý do sai: Không hiểu về hàm liên tục nên tính tích phân sai. Lời giải đúng: Áp dụng định lý về giá trị trung bình của tích phân, suy ra tồn tại ít b b nhất một điểm C a; b sao cho f x dx f c b a f c dx a a b c b Suy ra f x f c dx f x f c dx f x f c dx 0. a a c 11 Sai Lầm Khi Tính Tích Phân 5 http://megabook.vn/
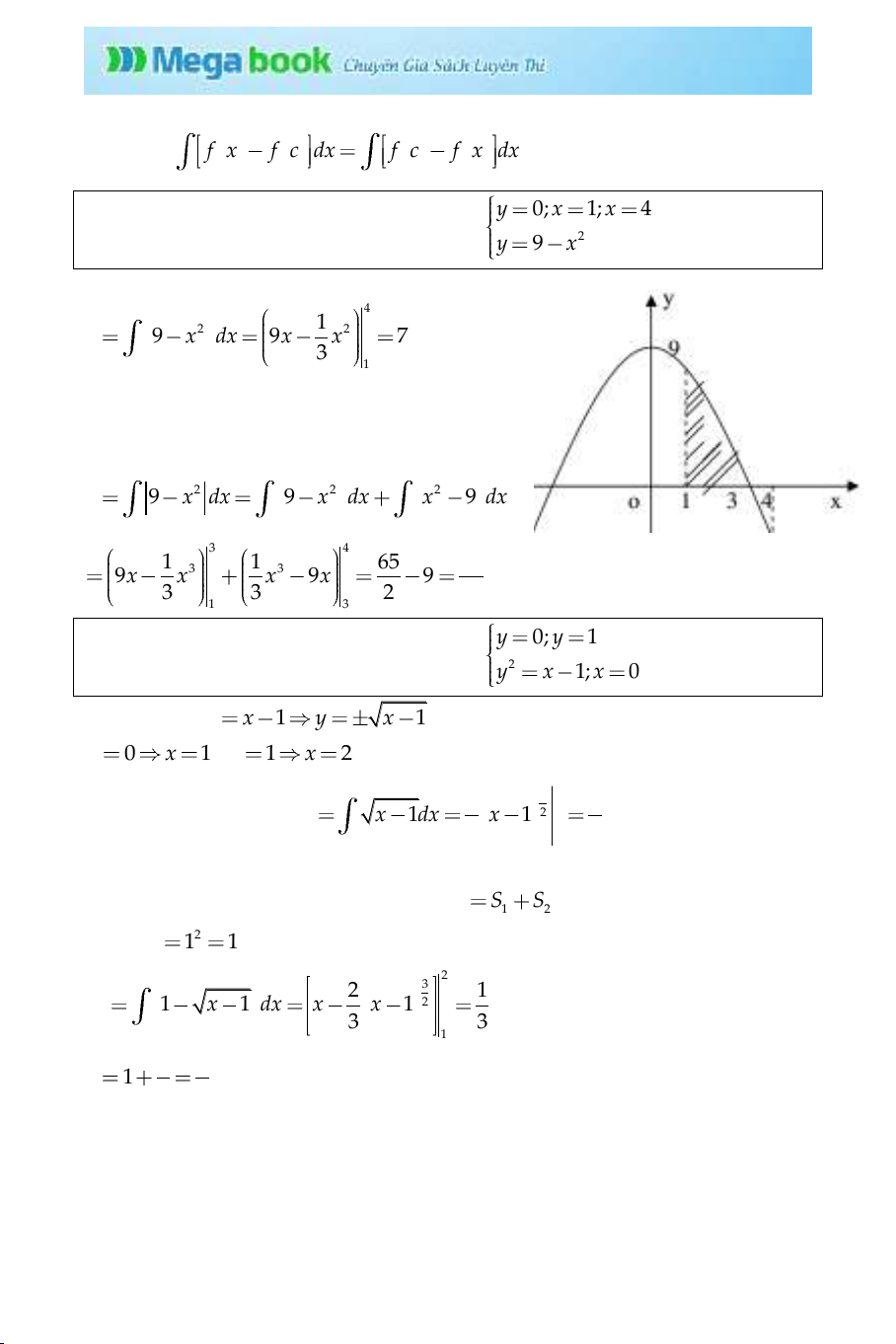
c b Hay ta có f x f c dx f c f x dx (đpcm). a c y 0; x 1; x 4 Bài 7. Tính diện tích hình phẳng giới hạn bởi 2 . y 9 x Lời giải sai: Diện tích hình phẳng là: 4 4 2 1 2 S 9 x dx 9x x 7. 1 3 1 Lý do sai: Áp dụng sai công thức, không ghi “đvdt – đơn vị diện tích”. Lời giải đúng: Diện tích hình phẳng là: 3 3 4 S 9 x 2 dx 9 x 2 dx x2 9 dx 1 1 3 3 4 1 3 1 3 65 38 9x x x 9x 9 (đvdt). 3 1 3 3 2 3 y 0; y 1 Bài 8. Tính diện tích hình phẳng giới hạn bởi 2 . y x 1; x 0 Lời giải sai: y 2 x 1 y x 1 y 0 x 1; y 1 x 2. 2 2 3 2 2 Diện tích hình phẳng là: S x 1dx x 1 2 (đvdt). 1 3 1 3 Lý do sai: Xác định sai hình cần tính diện tích. Lời giải đúng: Diện tích hình giới hạn là: S S1 S2 Ta có S1 12 1 (đvdt). 2 2 3 2 1 S2 1 x 1 dx x x 1 2 1 3 1 3 1 4 S 1 (đvdt). 3 3 11 Sai Lầm Khi Tính Tích Phân 6 http://megabook.vn/
y x2 2x 1 C1 Bài 9. Tính diện tích hình giới hạn bởi y x2 6x 9 C2 . 3 5 x ;x 2 2 Lời giải sai: C1 C2 2;1 . Vậy diện tích của hình giới hạn là: 5 2 2 2 2 S x 1 dx x 3 dx 3 2 2 5 2 1 3 1 3 2 x 1 x 3 3 3 3 2 2 1 1 1 1 7 (đvdt). 3 24 24 3 12 Lý do sai: Xác định sai hình cần tính giới hạn. Lời giải đúng: C1 C2 2;1 . Diện tích hình giới hạn là: S S1 S2 . 2 2 2 2 2 1 S1 x 3 x 1 dx 4x 8 dx 2x2 8x 3 3 3 2 2 2 2 5 5 2 2 5 2 2 1 S2 x 1 x 3 dx 4x 8 dx 2x2 8x 2 2 2 2 2 1 1 S S1 S2 1 (đvdt). 2 2 2 Bài 10. Tính thể tích hình xuyến gây bởi hình tròn x2 y b a2 ;( 0 a b) quay quanh trục Ox . Lời giải sai: Phương trình đường tròn 2 2 2 2 2 2 C :x y b a hay y b a x y b a2 x 2 C1 (x a ). y b a2 x 2 C2 11 Sai Lầm Khi Tính Tích Phân 7 http://megabook.vn/
Vậy thể tích của hình xuyến là: a 2 2 V b a2 x2 b a2 x2 dx 2 a2 b (đvtt). a b Lý do sai: Sai công thức tính thể tích: V y12 y22 dx mà là a b V ya2 y22 dx . a a 2 2 Lời giải đúng: V b a2 x2 b a2 x2 dx 2 a2 b . a y x2 Bài 11. Tính thể tích hình giới hạn bởi x 1 . x 2 2 2 x5 31 Lời giải sai: V x dx4 (đvtt). 1 5 1 5 b Lý do sai: Đã sử dụng công thức V y 2 dx . a 2 15 Lời giải đúng: V 2 x.x 2 dx (đvtt). 1 2 11 Sai Lầm Khi Tính Tích Phân 8 http://megabook.vn/