
Gv:Hoàng Hải-36a Trần Hưng Đạo-Hoàn Kiếm-HN
ĐT: 0932333922
203 BÀI TẬP HỆ PHƯƠNG TRÌNH
B ài` 1:Giải hệ phương trình:
2 2
3 3
30
35
x y xy
x y
ĐS:
2 3
3 2
x x
y y
Hướng dẫn : Đặt S=x+y, P=xy ( hệ đối xứng loại 1)
Bài 2: Giải hệ phương trình
3 3
2
2
( )xy x y
x y
ĐS:
1
1
x
y
HD: Đặt S=x-y, P=xy
Bài 3: giải hệ phương trình :
1 1 1 1
( ) ( ),P=(x+ )( )
x y y
x y x y
2 2
2 2
1 1 4
1 1
4
x y x y
x y x y
ĐS:
1
1
x
y
HD: Đặt S= 1 1 1 1
( ) ( ),P=(x+ )( )
x y y
x y x y
Bài 4:Giải hệ phương trình :
2 2
5
7
x y xy
x y xy
ĐS:
1 2
2 1
x x
y y
HD: Đặt S=x+y, P=xy
Bài 5: Giải hệ phương trình
2 2
3
2 2 3
x
x xy y
xy y
ĐS:
1 3 3
1
3 3
x x x
yy y
HD: Đặt S=x+y, P=xy
Bài 6: Giải hệ phương trình
3 3
2 2
8
xx y y
x y
ĐS:
2 0
0 2
x x
y y
HD: Đặt S=x+y,P=xy
Bài 7: Giải hệ phương trình
3 3
7
2
( )
x y
xy x y
ĐS:
1 2
2 1
x x
y y
HD: Đặt S=x-y, P=xy
Bài 8:Giải hệ phương trình
3
3
2
2
x
x y
y y x
ĐS:
0
0
x
y
HD: Lấy pt(1)-(2) làm xuất hiện nhân tử chung x-y (hệ phương trình đối xứng loại 2)

Gv:Hoàng Hải-36a Trần Hưng Đạo-Hoàn Kiếm-HN
ĐT: 0932333922
Bài 9:Giải hệ phương trình
2 3 4 4
2 3 4 4
xy
y x
ĐS:
11
3
9
3 11
9
x
x
yy
HD: Lấy pt(1)-(2) và trục căn thức làm xuất hiện nhân tử chung x-y
Bài 11: Giải hệ phương trình (ĐH Khối B-2003)
2
2
2
2
2
3
2
3
xx
y
y
yx
ĐS:
1
1
x
y
HD: lấy pt(1)-(2) làm xuất hiện nhân tử chung x-y
Bài 12:Giải hệ phương trình
2
1 1
2 1 0
x
x y
x y
xy
ĐS:
1 1
1 1
x x
y y
HD:từ pt(1) làm xuất hiện nhân tử chung x-y bằng cách chuyển vế và nhóm lại
Bài 13: Giải hệ phương trình
2
3 18 0
osx cos
x y c y
x y y
ĐS:
3
3
x
y
HD: (1)
x-cosx=y-cosy. Xét hàm số f(t)= t-cost
x=y
Bài 14: Giải hệ phương trình
2
2
3 2 0
3 2 0
x
x y
y
ĐS:
1 2
1 2
x x
y y
HD: lấy pt(1)-(2) làm xuất hiện nhân tử chung x-y
Bài 15: Giải hệ phương trình
2
2
2
2
x
x xy x y
y xy y
ĐS:
3
0
2
0 3
2
x
x
yy
HD: lấy pt(1)-(2) làm xuất hiện nhân tử chung x-y
Bài 16: Giải hệ phương trình
1 7 4
1 7 4
x y
y x
ĐS:
8
8
x
y
HD: lấy pt(1)-(2) và trục căn thức làm xuất hiện nhân tử chung x-y
Bài 17: Giải hệ phương trình
4 2
2 2
698
81
3 4 4 0
x
x y
x y xy y
ĐS:hệ vô nghiệm

Gv:Hoàng Hải-36a Trần Hưng Đạo-Hoàn Kiếm-HN
ĐT: 0932333922
HD: Từ pt(2) ta tìm được miền giá trị của x,y và kết hợp pt(1)
Bài 18:Giải hệ phương trình
3
3
2 3 1
2 3
( )
( )
x y
x y
ĐS:
1
1
2
1
2
xx
yy
HD: pt(1) chia cho
3
x
, pt(2) chia cho x sau đó lấy pt(1)+(2) ta được pt dạng
f(y)=f(
1
y
)
Bài 19: Giải hệ phương trình (HSG QG 1998-1999 Bảng A)
2 1 2 2 1
3 2
1 4 5 1 2
4 1 2 0
x x x
( )
x ln( )
y y y
y y x
ĐS:
0
1
x
y
HD: Từ pt(1) ta đặt t=2x-y và xét hàm số f(t)
t=1 sau đó thế vào pt(2) xét hàm f(y)
Bài 20: Giải hệ phương trình (HSG QG 2000-2001 Bảng B)
7 2 5
2 2
x x
x
y y
y x y
ĐS:
10 77
11 77
2
x
y
HD: Đặt u= 2 2
7 2 5
x ; v= x x
y y u v
và kết hợp với pt(1) 5
2
x
v
; kết
hợp pt(2)
x=2y-1
Bài 21: Giải hệ phương trình (HSG QG 1995-1996 Bảng A)
1
3 1 2
1
2 1 4 2
x( _ )
x( )
x y
x y
ĐS:
11 4 7
21
22 8 7
7
x
Y
HD: Xét đk sau đó chia 2 vế của hpt
3
x
và
2
y
, cộng trừ 2 vế sau khi ta được hệ
mới , lấy pt(1) nhân với pt(2) đưa về pt đẳng cấp với ẩn x,y
Bài 22: Giải hệ phương trình
2 2
3 2 16
2 4 33
x
x
xy y
x y y
ĐS:
3 3 3 3
2 3 2 3
x x
y y
HD: Đặt u=x-1; v=y-2 sau đó đặt u+v=S, uv=P
Bài 23: Giải hệ phương trình :
2 2 2 2
2 5 4 6 2 0
1
2 3
2
( x ) ( x ) ( x )
xx
y y y
yy
ĐS:
3
3
8
4
1
1
2
4
x x
y
y
HD: Pt(1) là pt đẳng cấp với ẩn 2x+y và 2x-y
Bài 23: Giải hệ phương trình

Gv:Hoàng Hải-36a Trần Hưng Đạo-Hoàn Kiếm-HN
ĐT: 0932333922
2 2
2 2
3 4 1
3 2 9 8 3
x
x x
x y y
y y
ĐS:
3 13 3 13
2 2
0 4
x x
y y
HD: Đặt u= 2 2
3 4
x; v=y
x y
Bài 24: Giải hệ phương trình
8
5
x x x y y y
x y
ĐS:
9
4
x
y
HD: Từ (1) nhóm lại và bình phương 2 vế sau đó thế phương trình (2) vào pt(1)
Bài 25: Giải hệ phương trình :
3 3
7
2
( )
x y
xy x y
ĐS:
2 1
1 2
x x
y y
HD: Đặt y=tx (hệ phương trình đẳng cấp )
Bài 26: Giải hệ phương trình
2 2
5
2 5 2
2
x
x xy y
y
x y xy
ĐS:
2 2
1 1
x x
y y
HD: Đặt y=tx (hệ phương trình đẳng cấp )
Bài 27: Giải hệ phương trình
2 2
2 2
2 3
10
( ) x
( )
y x y
x x y y
ĐS: 4 4
4 4
2 2
1 1
5 3 5 3
2 5 2 5
5 27 5 3
2 125 2 5
x x
y y
x x
y y
HD: : Đặt y=tx (hệ phương trình đẳng cấp )
Bài 28: Giải hệ phương trình
2 2
2 8 2
4
xx y y
x y
ĐS:
4
4
x
y
HD: Bình phương pt(2)rút x+y thay vào pt(1) và đặt t=
xy
Bài 29: Giải hệ phương trình
30
35
x y y x
x x y y
ĐS:
4 9
9 4
x x
y y
HD: Đặt ;u x v y
hpt với ẩn u,v ( hệ đối xứng loại 1)
Bài 30: Giải hệ phương trình
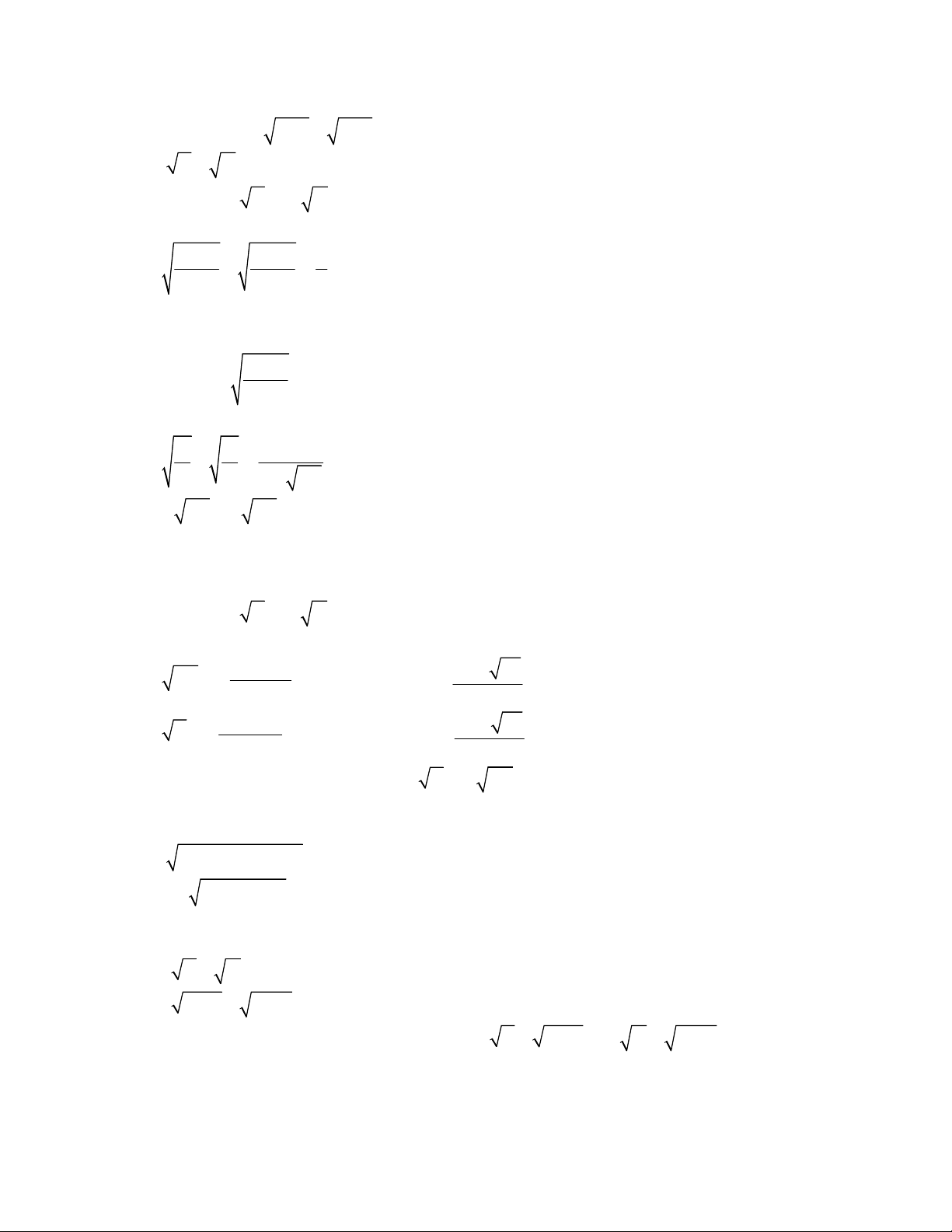
Gv:Hoàng Hải-36a Trần Hưng Đạo-Hoàn Kiếm-HN
ĐT: 0932333922
2 2
3 3
33
2 3
6
( ) (
x y x y y x
x y
ĐS:
8 64
64 8
x x
y y
HD: Đặt 33
, v=
u x y
hpt với ẩn u,v ( hệ đối xứng loại 1)
Bài 31: Giải hệ phương trình
6 5
6 2
9
x
x
x y
x y
x y xy
ĐS: hệ vô nghiệm
HD: Đặt u= 6
x
x y
u từ pt(1)
Bài 32: Giải hệ phương trình
7
2
7
0,
x y
y x
xy
x xy y xy
x y
ĐS: hệ vô nghiệm
HD: Đặt ,u x v y
hpt với ẩn u,v (hệ đối xứng loại 1)
Bài 33: Giải hệ phương trình
5
2 3 4
42
5
3 2
42
( )
x
( )
yy
xx y
ĐS:
5 2 26
27
5 2 26
9
x
y
HD: Xét đk sau đó chia 2 vế của hpt
x
và
2
y
. Cộng trừ 2 vế sau khi chia ta được hệ
mới , lấy pt (1) nhân với pt(2) đưa về pt đẳng cấp với ẩn x,y
Bài 34:Giải hệ phương trình
2 4 2 4 2 2
2 3 3 2
3 2 1 2
1 1 2
( x )
( ) ( )
x y x y x y
x y x x x y
ĐS:
1
1
x
y
HD: Cộng 2 vế của 2 pt với nhau sau đó đánh giá 2 vế của pt mới
Bài 35: Giải hệ phương trình
10
6 6 14
x y
x y
ĐS: Hệ vô nghiệm
HD: lấy pt(1)
pt(2) ta được hpt mới . Đặt u=
6 6
; v=x x y y
( hệ đối
xứng loại 1 với ẩn u,v)
Bài 36: Giải hệ phương trình













![Đề thi Toán vào lớp 10 năm 2022-2023 Sở GD&ĐT Cần Thơ (Khối chuyên) - [Kèm đáp án chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2022/20220610/britaikridanik/135x160/1982848550.jpg)









![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)










![Phiếu bài tập cuối tuần Tiếng Việt 1 tuần 2 đề 2: [Hướng dẫn chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250728/thanhha01/135x160/42951755577464.jpg)
