1
Chương 3. Cân bằng của vật rắn -
Chương
3
Cơ học kỹ thuật: TĨNH HỌC
Engineering Mechanics: STATICS
Cân bằng của vật
rắn và hệ vật rắn
Nguyễn Quang Hoàng
Bộ môn Cơ học ứng dụng
Chương 3. Cân bằng của vật rắn - -2-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Nội dung
3.0 Điều kiện cân bằng của vật rắn
3.1 Cân bằng của vật rắn phẳng
1. Điều kiện cân bằng và phương trình cân bằng
2. Các loại liên kết / Sơ đồ giải phóng liên kết
3. Phần tử hai lực và phần tử ba lực
4. Cân bằng của hệ vật rắn phẳng
5. Tính xác định tĩnh
3.2 Cân bằng của vật rắn không gian
1. Điều kiện cân bằng và phương tình cân bằng
2. Các loại liên kết / Sơ đồ giải phóng liên kết
3. Các ví dụ
3.3 Phân tích hệ thanh
Chương 3. Cân bằng của vật rắn - -3-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Điều kiện cân bằng tổng quát cho vật rắn
z
F4
F1
F2F3
y
O
x
Cj
C1
0,
() 0,
Ok
OOk j
RF
MmFC O

 


Vật rắn tự do cân bằng hệ lực tác
dụng lên vật là hệ lực cân bằng.
12 1
( , ,..., , ,..., ) 0
nm
FF FC C

12 1
( , ,..., , ,..., ) ( , ) 0
nmOO
FF FC C R M


2
Chương 3. Cân bằng của vật rắn - -4-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
CÂN BẰNG CỦA VẬT RẮN PHẲNG
1. Điều kiện cân bằng và PTCB
2. Các loại liên kết / Sơ đồ giải phóng liên kết
3. Phần tử hai lực và phần tử ba lực
4. Cân bằng của hệ vật rắn phẳng
5. Tính xác định tĩnh
Chương 3. Cân bằng của vật rắn - -5-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Điều kiện cân bằng và phương trình cân bằng của hệ lực phẳng
y
F4
F1
F2
F3
x
O
Cj
0, (1)
0, (2)
() 0 (3)
kx
ky
Ok j
F
F
mF C



0
() 0,
Ok
OOk j
RF
MmFC O

 

Dạng 1.
0, (1)
() 0 (2)
() 0 (3)
( khong AB)
kx
Ak j
Bk j
F
mF C
mF C
x



Dạng 2. Dạng 3.
() 0 (1)
() 0 (2)
() 0 (3)
(A, B,C khong thang hang)
Ak j
Bk j
Ck j
mF C
mF C
mF C



Chương 3. Cân bằng của vật rắn - -6-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Phương trình cân bằng của hệ lực phẳng
Dạng hệ lực Hình vẽ Số PT
CB Các PT cân bằng
Hệ lực
phẳng tổng
quát
3
Hệ lực
phẳng đồng
qui
2
yF1
F2
F3
x
O
Cj
y
F1
F2
F3
x
O
0,
0,
0,
kx
ky
Oj
F
F
MC



0,
0,
kx
ky
F
F


3
Chương 3. Cân bằng của vật rắn - -7-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Phương trình cân bằng của hệ lực phẳng
Dạng hệ lực Hình vẽ Số PT
CB Các PT cân bằng
Hệ ngẫu lực
phẳng 1
Hệ lực song
song y
2
y
F1
F2
F3
x
O
0
k
C
0
0
ky
O
F
M


yC1
C2
C3
x
O
Chương 3. Cân bằng của vật rắn - -8-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Các loại liên kết phẳng / Giải phóng liên kết
F
Dây (lk một phía)
F
Con lăn (gối di động),
(lk một phía)
F
Tựa trơn nhẵn (lk một phía)
F
F
or
Con lăn trong rãnh
(lk hai phía)
Tựa trơn nhẵn (lk một phía)
N2
N1
N2
N1
Chương 3. Cân bằng của vật rắn - -9-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Các loại liên kết phẳng / Giải phóng liên kết
F
F
or
Nối bản lề với con trượt
(tựa 2 phía)
Fx
Fy
F
or
Bản lề (gối cố
định)
o
r
Fx
F
y
M
M
F
ngàm
F
Iên kết thanh
F
F
4
Chương 3. Cân bằng của vật rắn - -10-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
P
P
N1N2
N
M
P
Ổ đỡ ngắn (như tựa 2 phía)
Ổ đỡ dài (như ngàm trượt)
N2
N1
Chương 3. Cân bằng của vật rắn - -11-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Các loại liên kết / Giải phóng liên kết
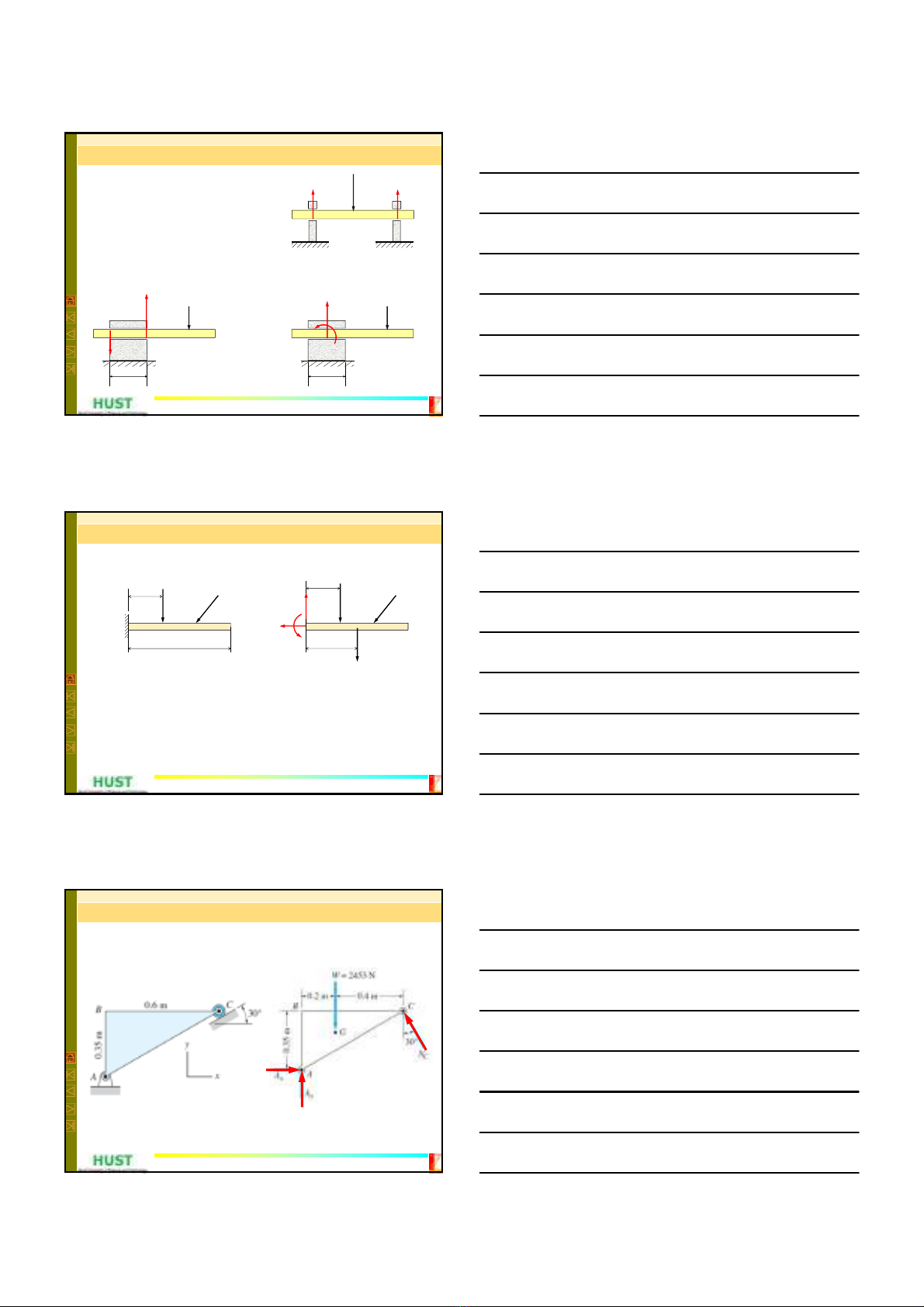
Ví dụ. Vẽ sơ đồ giải phóng liên kết cho dầm đồng chất khối lượng 100 kg
chịu liên kết ngàm tại đầu A.
Lời giải
- Vẽ tách dầm khỏi ngàm
- Vẽ các lực đã cho
- Vẽ các lực/ ngẫu lực thay thế cho liên kết: Ax, Ay, MA(hoặc XA, YA, MA).
Độ lớn chưa biết, còn chiều được giả định.
- Trọng lượng Wđặt tại giữa dầm.
- Sơ đồ giải phóng liên kết được vẽ ra như trên hình.
2 m
6 m
1200 N
(a)
A
Ay
Ax
MA
(b)
Fig. 3-9
200 N
2 m
3 m
1200 N
981 N
200 N
Chương 3. Cân bằng của vật rắn - -12-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Ví dụ. Vẽ sơ đồ giải phóng liên kết cho tấm tam giác đồng chất khối
lượng 250 kg chịu liên kết bản lề tại A và con lăn tại C như trên hình.
5
Chương 3. Cân bằng của vật rắn - -13-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Ví dụ : xác định phản lực liên kết
Dầm có liên kết và chịu tải như hình vẽ.
Xác định lực liên kết tại A và B. Bỏ qua
trọng lượng của dầm.
Sơ đồ giải phóng liên kết
Gối di động A: 01 thành phần lực Ay
Gối cố định B (bản lề cố định): 02
thành phần lực: Bx, By
2 m
600 N
2 m3 m
45o
100 N
AB
D
200 N
0.2 m
2 m
F1, 600 N
2 m3 m
45o
F2, 100 N
AB
D
F3, 200 N
0.2 m
AyBy
Bx
Hệ lực cân bằng
123
(, , , , , ) 0
yxy
FFFAB B

Chương 3. Cân bằng của vật rắn - -14-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Ví dụ : xác định phản lực liên kết
Các phương trình cân bằng
0 : 600 cos 45 0
0 : 600 sin 45 100 200 0
0 : 100 2 600 sin 45 5 600 cos 45 0.2 7 0
o
xx
o
yy y
oo
B y
FB
FA B
MA



319 N, 424 N, 405 N
yxy
ABB
Giải hệ nhận được
2 m
600 N
2 m3 m
45o
100 N
AB
D
200 N
0.2 m
AyBy
Bx
Chương 3. Cân bằng của vật rắn - -15-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Ví dụ : xác định phản lực liên kết
AB
C
D
P
a b
A
B
C
D
P
ab
TCD
YA
XA
Dầm AB được giữ ngang nhờ gối A và dây
CD. Xác định lực liên kết tại A và lực căng dây
Sơ đồ giải phóng liên kết
Dây DC: 01 thành phần lực TCD
Gối cố định A (bản lề cố định): 02
thành phần lực: XA, YA
Hệ lực cân bằng
(, , , ) 0
CD A A
PT X Y

sin 0,
cos 0
() cos ( ) 0
kx A CD
ky A CD
Ak CD
FXT
FYT P
mF aT a bP



PT cân bằng
()
,
cos
()
tan ,
CD A
A
ab b
TPYP
aa
ab
XP
a
