Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 5
9/29/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
2. Ứng suấttổng quát và các thành phầnứng suất
NỘIDUNG
3. Trạng thái ứng suấtsuấtphẳng
4. Các thuyếtbền
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Ứng suấtvàbiếndạng đơntrục
Bộphậnhạcánh chịusựnén Thanh nốichịusựkéo
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 5
9/29/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
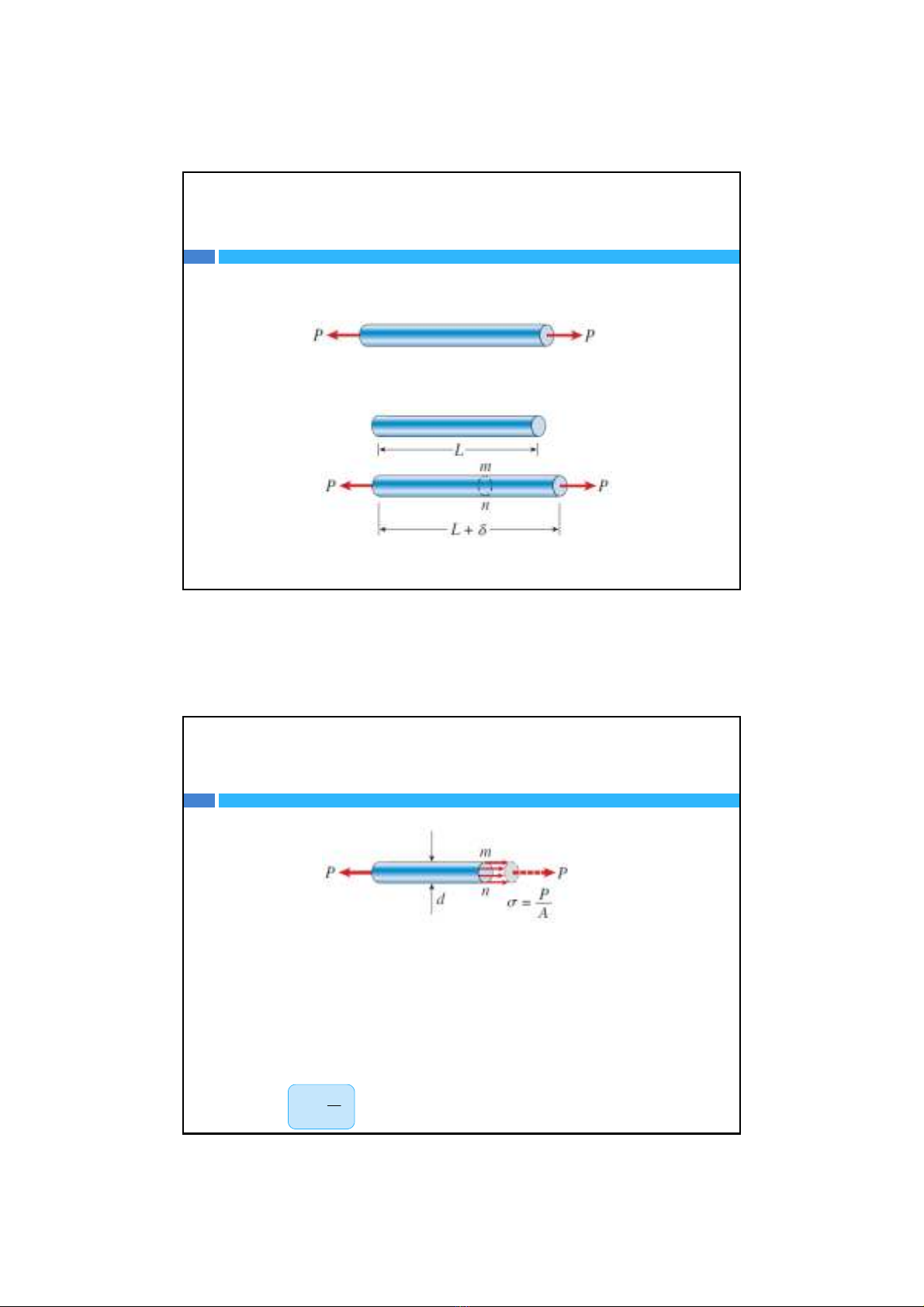
Ta xét thanh nốigiữaxekéovàmáybay,giảsửbỏqua khốilượng của
thanh và thanh nốichỉchịulực tác dụng dọctrụcvớilựcởhai đầu thanh
là P
Trướckhitácdụng lựcP,thanhcóchiều dài L. Sau khi tác dụng lựcdọc
trục P, thanh có chiềudàiL+,vậylà độ giản dài so vớichiều dài ban
đầu.
Để khảo sát thành phầnnộilực trong thanh ta dùng mộtmặtcắtmncắt
vuông góc vớitrục thanh
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
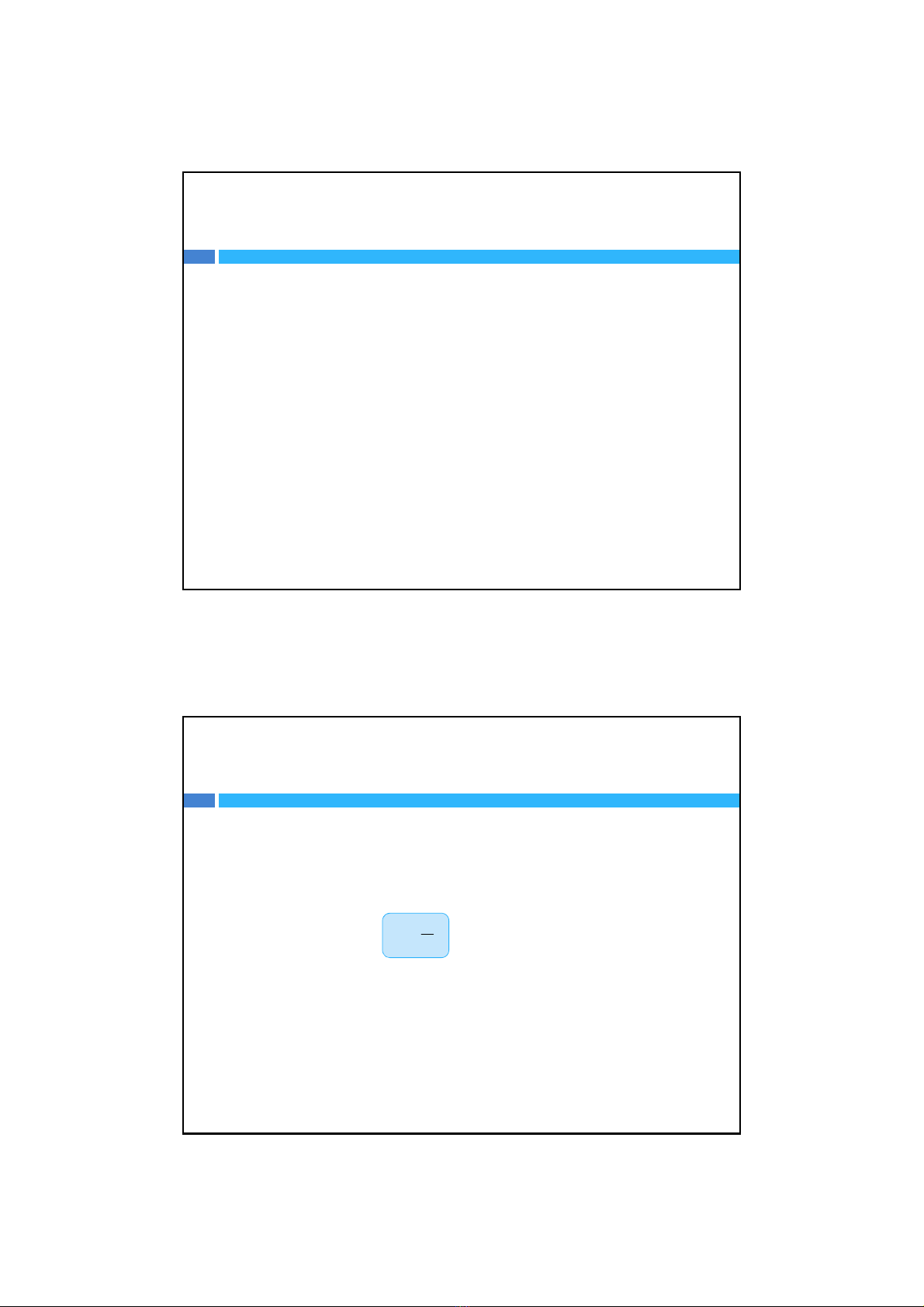
Bây giờta xét thành phần bên trái củamặtcắtmnnhưlà mộtvậtthểtựdo
Khi xét phần bên trái mặtcắt, ta sẽcó thành phầnứng suất phân bốliên tục
tác dụng lên mặtcắt và chính thành phầnnộilựcdọctrụccóđộ lớnbằng P
là lựctổng hợpcủa thành phầnứng suấttrên.
Ứng suấtcóđơnvịlà lựctrênmộtđơnvịdiệntíchvàđượckýhiệulà
(sigma). Giảsửứng suất tác dụng lên mặtcắtmnđược phân bốđềutrên
miềndiệntích.Nênnộilựctổng hợpcủaứng suấtcóđộ lớnbằng độ lớn
củaứng suấtnhânvớidiệntíchmặtcắtA,P=
A.Dođótađượccôngthức
tính độ lớnứng suất:
P
A
Công thức này tính đượccường độ ứng suấtcủalực
dọctrụctrênmiềndiện tích có hình dạng bấtkỳ.
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 5
9/29/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Khi thanh giãn ra bởilựckéoPthìứng suất sinh ra là ứng suấtkéo.Nếutác
dụng lực theo chiềungượclại làm thanh chịunénthìứng suất sinh ra là
ứng suấtnén.
Do phương củaứng suấtvuônggócvớimặtcắtnêntagọiđây là ứng suất
pháp tuyến. Ta sẽcó ứng suất pháp có thểlà ứng suấtkéohoặccũng có thể
là ứng suất nén. Thành phầnứng suất pháp tuyếnsẽmang dấudương (+)
khi thanh chịukéovàâmkhithanhchịunén.Trongphầnsauchúngtasẽ
xét thêm một thành phầnứng suấtkhácnữalàứng suấttiếp(hoặcứng
suấtcắt), ứng suấtnàysẽnằm song song vớimặtcắt.
Khi ta sửdụng hệđơnvịSI thì đơnvịcủalựclà(N),diệntíchlà(m
2). Vì thế
ta có đơnvịcủaứng suấtlà(N/m
2)bằng vớiđơnvị(Pa), (N/mm2)bằng với
đơnvị(MPa).
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Theo hình ta thấyvớimột thanh thẳng chịu tác dụng củalựcdọctrụcthì
chiều dài thanh sẽthay đổi, thanh sẽdài hơnkhichịukéovàngắnhơnkhi
chịunén,độ thay đổichiều dài này là
.Độ giãn dài tỉđốicủa thanh sẽtính
bằng độ thay đổichiềudài
chia cho chiều dài ban đầucủathanhvàđại
lượng này đượcgọilàbiếndạng
L
Nếu thanh chịukéothìbiếndạng này là biếndạng kéo, điềunàychothấy
độ dài của thanh sẽtăng. Nếuthanhchịunénthìbiếng dạng này là biến
dạng nén, chiềudàithanhsẽngắnlại. Vì hệsốbiếndạng là tỉsốcủahai
chiều dài nên đơnvịcủabiếndạng là vô thứnguyên.
Giảsửsựdịch chuyểntrênthanhlàđồng nhất trên toàn thanh, lựcdọctrục
tác động vào thanh tạitrọng tâm củadiệntíchmặtcắtvàvậtliệuđồng
nhất. Kếtquảcủatrạng thái này đượcgọilàtrạng thái ứng suấtbiếndạng
đơntrục.
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 5
9/29/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Đàn hồituyến tính,định luật Hookevà hệsốPoisson
Rất nhiềuvậtliệukếtcấu(kimloại, gỗ,nhựavàsứ)đềucógiaiđoạnđàn
hồituyếntínhkhigiatảilầnđầu. Theo đó, đường cong ứng suấtbiếndạng
sẽbắtđầulàmộtđường thẳng và đitừgốctọađộ.
Khi vậtliệuứng xửtrong miềnđàn hồivàmối quan hệgiữaứng suấtvà
biếndạng là tuyếntínhthìgọiđây là đàn hồituyến tính. Loạiứng xửnày rất
quan trọng trong kỹthuậtbởivìkhithiếtkếmộtkếtcấuhoặcmột cái máy
sẽnằmtrongmiềnnàyđể tránh sựbiếndạng dẻocủavậtliệu.
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Ví dụđường cong ứng suấtbiếndạng củavậtliệuthép
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 5
9/29/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Định luật Hooke
Mối quan hệtuyếntínhgiữaứng suấtvàbiếndạng cho
mộtthanhchịukéohoặcchịunénđượcbiểudiễnbằng
công thức
E
Với
là ứng suấtdọctrục,
là biếndạng dọctrụcvà E
là hằng sốtỉlệđượcgọilàmô‐đun đàn hồicủavậtliệu.
Mô‐đun đàn hồilàđộ dốccủađường cong ứng suất
biếndạng trong giai đoạnđàn hồituyếntính
RobertHooke(1635‐
1703)là nhà khoa họcnổi
tiếng người Anh.Là người
đầu tiên khám phá vật
liệuđàn hồivàđãthí
nghiệm nhiềuloạivậtliệu
nhưkim loại,gỗ,đá,
xương và gân
Công thứctrênlàcôngthứcđơngiảncủađịnh luật
Hooke chỉsửdụng để tìm ứng suấtvàbiếndạng dài cho
trường hợpthanhchịukéovànén(đơntrục). Những
trạng thái ứng suấtphứctạphơntasẽkhảosáttrong
phầnsau
CHƯƠNG 4 Ứng suấtvàbiếndạng
1. Khái niệmcơbảnvềsựkéo, sựnén và sựcắt
Hệsốmô‐đun đàn hồicònđượcgọilàhệsốYoung do
mộtnhàkhoahọcngườiAnhkháctìmratừcác thanh
chịukéovàchịunén.
Để tìm hệsốmô‐đun đàn hồitasửdụng máy kéo nén
ThomasYoung(1773‐
1829)là nhà khoa học
nổitiếng ngườiAnh