Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng- Tuần 3
9/8/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
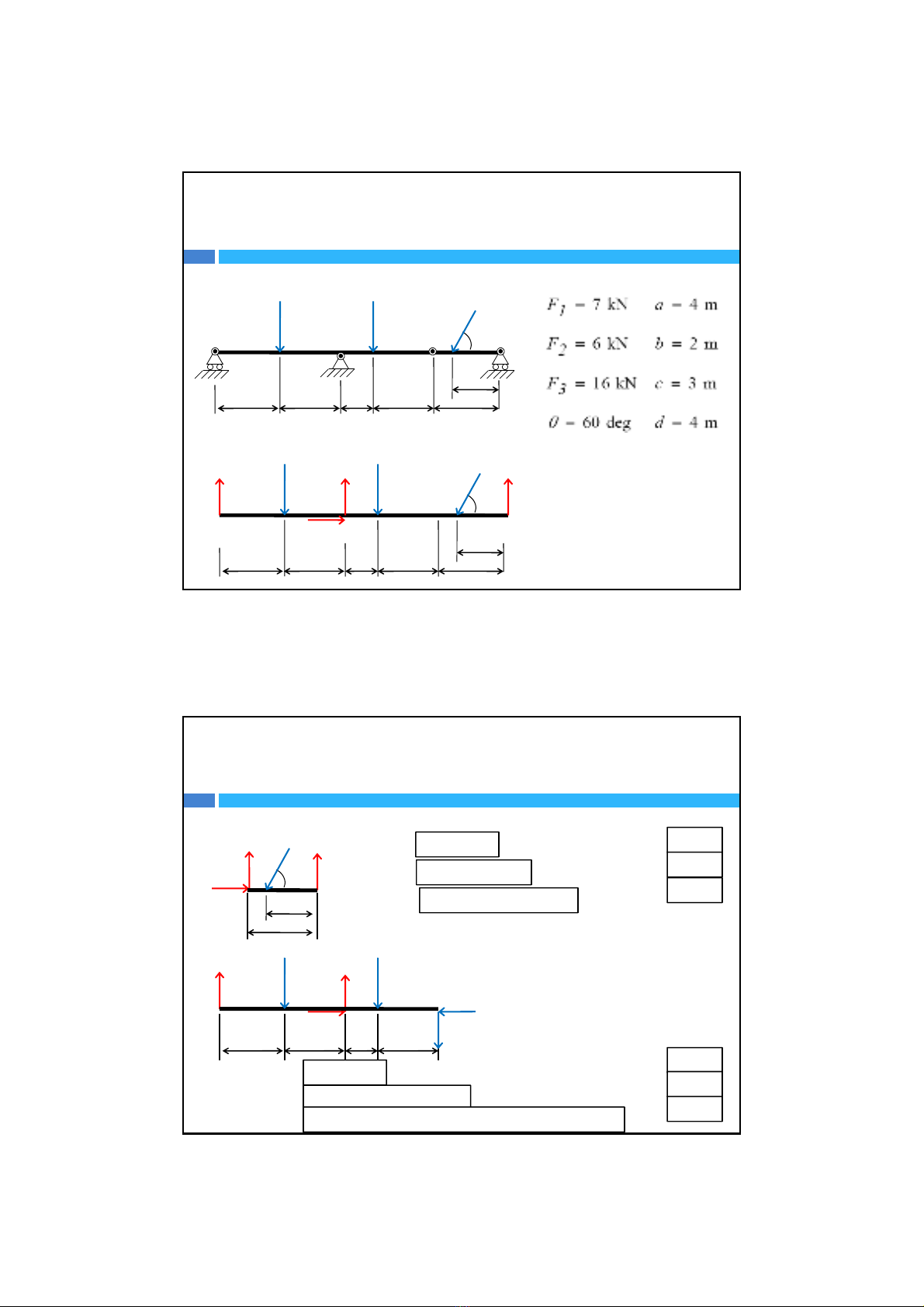
Ví dụ: Tìm phảnlực liên kết
Ba phương trình bốnẩn!!!
F3
a
F2
F1
ABC
D
aaa
c
b
ABC
D
F3
F2
F1
aaaa
c
b
Ay
By
Bx
Cy
Hóa rắn vật, xét ADC cân bằng
CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
1
1
1
cos 0
sin 0
sin ( ) 0
kx
ky
D
x
yy
y
FF
FF
Ma
D
DC
CFac

1.52
3.5
4.55
y
x
y
CkN
D
kN
D
kN

23
23
0
0
2(3)(2) 0
kx x
ky y
x
y
y
y
Ay
B
AB
B
FD
FDFF
MaDabFabFa
3.09
3.5
23.5
y
x
y
A
kN
B
kN
B
kN

Dy
Dx
Cy
Xét thanh CD cân bằng
AyBy
Bx
C
D
F1
a
c
Xét thanh AD cân bằng
AB
F3F2
aaa
b
D
Dy
Dx
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng- Tuần 3
9/8/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
Ví dụ: Tìm phảnlực liên kếttại A, B, C
CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
Ví dụ: Tìm phản lực liên kết
F
M
q
45o
A
B
C
222AB BD BC a m

2
M
qa
2
F
qa
10 /qKNm
Tìm phản lực liên kết tại A và D.
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng- Tuần 3
9/8/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
Phân tích: 4 ẩn mà ta chỉ có 3 phương trình nên không giải nguyên
vật được mà phải TÁCH VẬT
+Xét thanh BD cân bằng:
F
M
B
D
C
D
N
x
B
y
B
0
0
220
2
x
y
B
x
Dy
D
FF
F
a
MMF
B
NB
Na

20( )
17, 07( )
17, 07( )
x
y
D
KN
K
N
K
N
B
B
N

+Xét thanh AB cân bằng:
q
A
B
x
B
y
B
x
A
y
A
A
M
2
0
20
22 0
xx
yy
y
yAA
x
FB
FBqa
MMq
A
Ba
A
a

20( )
2,93( )
14,14( . )
x
y
A
A
A
KN
KN
Km
MN

CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
Ví dụCho cơcấucóliênkếtchịulựcnhưhình vẽ. Thanh CDtựalên
thanh AB tạiB,biết AB=BC=2BD=2a, F=qa.
1) Hệcó luôn cân bằng vớimọiloạitảitácđộng hay không? Vì sao?
2) Tìm phảnlực liên kếttạiAvàCtrongcáctrường hợpsauđây
a) VớiM=qa2.
b) VớiM=3qa2.
AB
q
F
C
D
M
45o
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng- Tuần 3
9/8/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
* Tính bậctựdo củahệ
3 32320,5dof n R
 0, 5 0dof
Bậctựdo củacơhệdương nên hệkhông luôn cân bằng vớimọi
loạitảitácđộng
* Để khảosátsựcân bằng củahệthì thanh CD phảicânbằng
Để thanh CD cân bằng thì phảnlựctạiN
B>0
B
F
C
D
M
45o
x
C
y
C
B
N
+Xét thanh CD cân bằng:
20
2
20
2
32 20
2
x
y
C
x
y
B
B
B
N
FF
F
a
MM
CN
Na
C
F

32
42
2
4
32
4
y
B
x
M
Fa
Fa M
a
Fa
a
C
C
N
M

CHƯƠNG 2 Thu gọnhệlực, điềukiệncânbằng
2. Điềukiệncânbằng củahệ
AB
q
x
A
y
A
A
M
B
N
* Để thanh CD luôn tựa vào thanh AB 320
42
B
M
F
Na
2
32
2
M
qa
* Xét thanh AB cân bằng
20
2
2
.2 0
2
2
.2 . 2 0
2
xB
yB
A
x
B
y
A
FN
FqaN
MqaaN
M
A
a
A

2
32
4
(5 2)
4
12
2
x
y
A
A
M
qa
qa
qa
A

a) VớiM=qa2nên thanh CD luôn tựa vào thanh AB
AB
q
x
A
y
A
A
M
0
.2 0
.2 . 0
x
y
A
y
A
x
A
F
A
M
Fqa
Mqaa

2
0
2
2
x
y
A
A
M
qa
qa
A


b) VớiM=3qa2nên thanh CD không tựa vào thanh AB nên NB=0