Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 4
9/20/2011
Giảng viên Nguyễn Duy Khương 1
Phần2:Cơhọcvậtrắnbiếndạng
Chương 3: Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
Chương 4: Ứng suấtvàbiếndạng
Chương 5: Tính bềncácbàitoánthuộcdạng thanh
Chương 6: Tính biếndạng của thanh
Chương 7: Tính hệsiêu tĩnh
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
1. Giớithiệuvềcơhọcvậtrắnbiếndạng đàn hồi
2. Trạng thái cân bằng củavậtthểbiếndạng
NỘIDUNG
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 4
9/20/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
1. Giớithiệuvềcơhọcvậtrắnbiếndạng đàn hồi
•Cơhọcvậtrắnbiếndạng đàn hồilà một nhánh củangànhCơ
học nghiên cứunhững ảnh hưởng củaứng suấtvà biếndạng
tác động lên cấutrúcbêntrongvậtthểrắndướitácdụng của
ngoạilực.
•Từđạilượng ứng suất,tacóthểtính đượcđộ bềncủavậtliệu.
Trong khi đó, đạil
ượng biếndạng được dùng để tính chuyểnvị
củavậtliệu.
•Việchiểukháiniệmvềmôn họcmột cách rõ ràng là rất quan
trọng bởivìnhiềucôngthứcvàcácđịnh luậtđể thiếtkếtrong kỹ
thuậtlàdựatrênnhững nguyên lý củamônhọcnày.
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
1. Giớithiệuvềcơhọcvậtrắnbiếndạng đàn hồi
Lịch sửphát triển
•Vào đầuthếkỷ17, Galileo đãthựchiện nhiều thí nghiệmvềảnh
hưởng củatảitrọng lên thanh và dầmđượclàmtừnhiềuvật
liệu khác nhau. Tuy nhiên, vào đầuthếkỷ18, nhiềuphương
pháp thí nghiệmvềkiểmtravậtliệuđượccảitiếnởkhắpnơi,
đặcbiệtlàởPháp, có những nhà Cơhọcnổitiếng nhưSaint‐
Venant, Poisson, Lamé và Navier.
•Trải qua nhiềun
ăm, sau khi giải quyết nhiềubàitoáncơbảncủa
cơhọcvậtliệu, nó cầnphảisửdụng toán họcvàkỹthuậtmáy
tính cao cấpđể giảicácbàitoánphứctạphơn. Kếtquảlà từlĩnh
vựcnàymởra nhiềulĩnh vực khác nhau thuộcngànhcơhọcnhư
là lý thuyếtđàn hồi, lý thuyếtdẻo. Những nghiên cứutrong
nhiềulĩnh vựcvẫncứtiếptụcđể giải quyếtcácbàitoánphức
tạphơntrongkỹthuật.
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 4
9/20/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
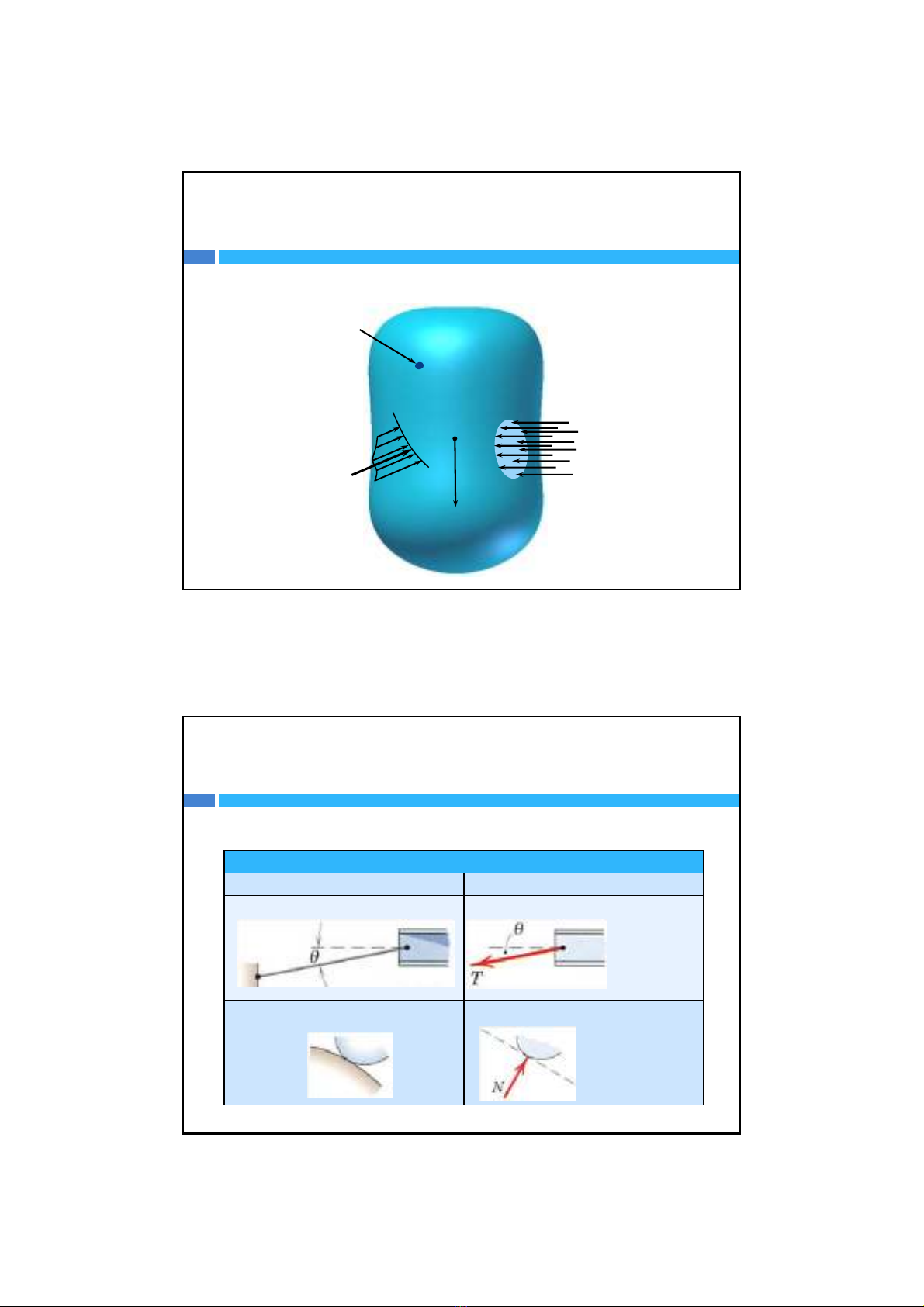
2. Trạng thái cân bằng củavậtthểbiếndạng
Ngoạilực
Lực
bề
mặt
Lực
tập
trung
w(x)
FR
Lực phân bố
trên đường P
Lực
khối
G
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
2. Trạng thái cân bằng củavậtthểbiếndạng
Phảnlực liên kết
Bảng 1.1
Loại liên kếtPhảnlực
1.Dây cáp,xích hoặc thanh Sợidâyluôn
căng có lực
căng dây dọc
theo phương
củadây
2.Tiếp xúc nhẵnLựctương tác
giữa2bềmặt
nhẵnlàlựcnénvà
có phương vuông
góc bềmặt
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 4
9/20/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
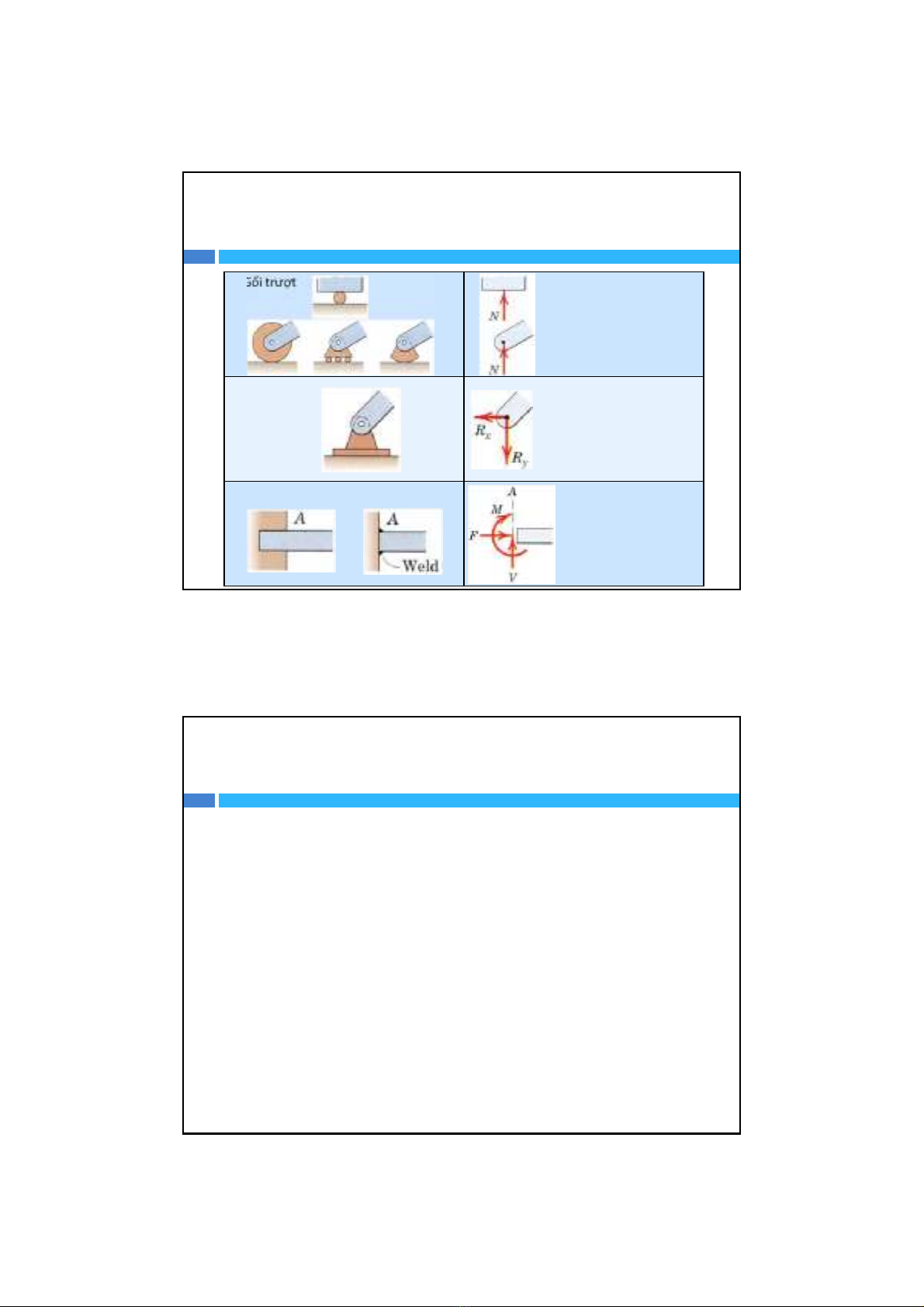
2. Trạng thái cân bằng củavậtthểbiếndạng
3.Gốitrượt
4.Gốicốđịnh
5.Ngàm
Lực vuông góc vớibề
mặtgốitrượt
Mộtlựccóhướng bấtkỳ
nằmtrongmặtphẳng
vuông góc vớitrục quay,
thông thường taphân tích
thành hai thành phầnR
x,Ry
Liên kếtngàmbaogồm
phảnlựcdọctrụcF,
phảnlựclựccắtVvà
phảnlựcmômentMđể
cảntrởchuyểnđộng
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
2. Trạng thái cân bằng củavậtthểbiếndạng
Phương trình cân bằng
0
0
O
R
R
F
M


0
0
0
()0
()0
()0
kx
ky
kz
xk
yk
zk
F
F
F
mF
mF
mF
Trong không gian 2chiều:
0
0
()0
kx
ky
Ok
F
F
mF
Việcsửdụng phương trình cân bằngcóthànhcônghaykhôngcònphụ
thuộcvàoviệc phân tích các ẩnsốlà các phảnlực liên kết
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 4
9/20/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
2. Trạng thái cân bằng củavậtthểbiếndạng
F1
F2
O
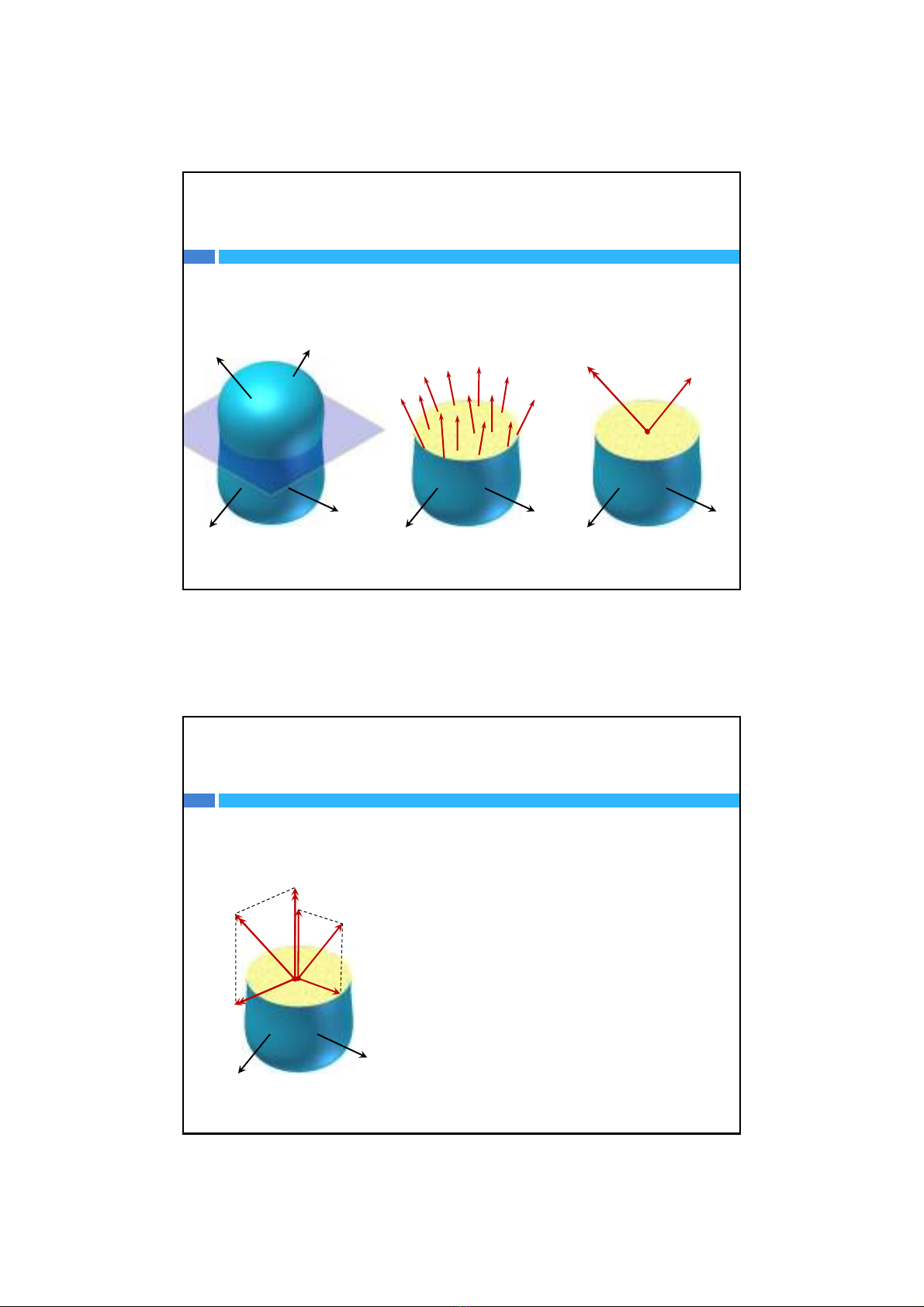
Nộilựctổng hợp
Xét vậtthểchịu4
lực cân bằng
F1
F2
F4
F3
Dùng mộtmặtcắt
cắtđôi vậtthểđể
xét nộilực
F1
F2
Thugọnnộilựcvề
điểmOlà trọng tâm
củamặtcắt
MRO FR
Trong bài toán thanh và dầmthìmặtcắtsẽvuông góc vớitrụccủa thanh và dầm.
CHƯƠNG 3 Khái niệmcơbảnvềvậtrắnbiếndạng đàn hồi
2. Trạng thái cân bằng củavậtthểbiếndạng
Trong không gian ba chiều
Phân tích MRO và FRthành các thành phần vuông góc và nằmtrongmặtcắt
F1
F2
MRO FR
O
N
Q
M
TLựcdọctrục, N :làlựcvuônggócvớimặtcắt. Lực
này xuấthiệnkhingoạilực tác dụng làm hai phần
củavậtthểbịkéo hoặcnén.
Lựccắt, Q :làlựcnằmtrongmặtcắt. Lựcnàyxuất
hiệnkhingoạilực tác dụng làm hai phầncóxu
hướng trượt nhau.
Moment xoắn, T :làmomentvuônggócvớimặt
cắt. Moment này xuấthiện khi ngoạilực làm một
phầncủavậtthểxoắn quanh mộttrục vuông góc
vớimặtcắt.
Moment uốn, M :làmomentnằmtrongmặtcắt.
Moment này xuấthiệnkhingoạilực làm uốnvật
thểquanh trụcnằmtrongmặtphẳng cắt.