Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 9
11/13/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
I‐Thanh chịuuốn ngang phẳng
Trên mặtcắtchỉcó hai thành phầnnộilựclàlực
cắtQ
yvà mô‐men Mx.Dođótrạng thái ứng suất
trong thanh có hai thành phầnlàứng suất pháp z
và ứng suấttiếpzy (có thểcó ứng suấttiếpzx
nhưng do giá trịthường nhỏhơnzy nên ta bỏ
qua)
B‐Thanh chịulựcphứctạp
Trong trường hợptổng quát, trạng thái ứng suất
củađiểmtrongthanhchịuuốn ngang phẳng ở
trang thái ứng suấtphẳng đặcbiệt.
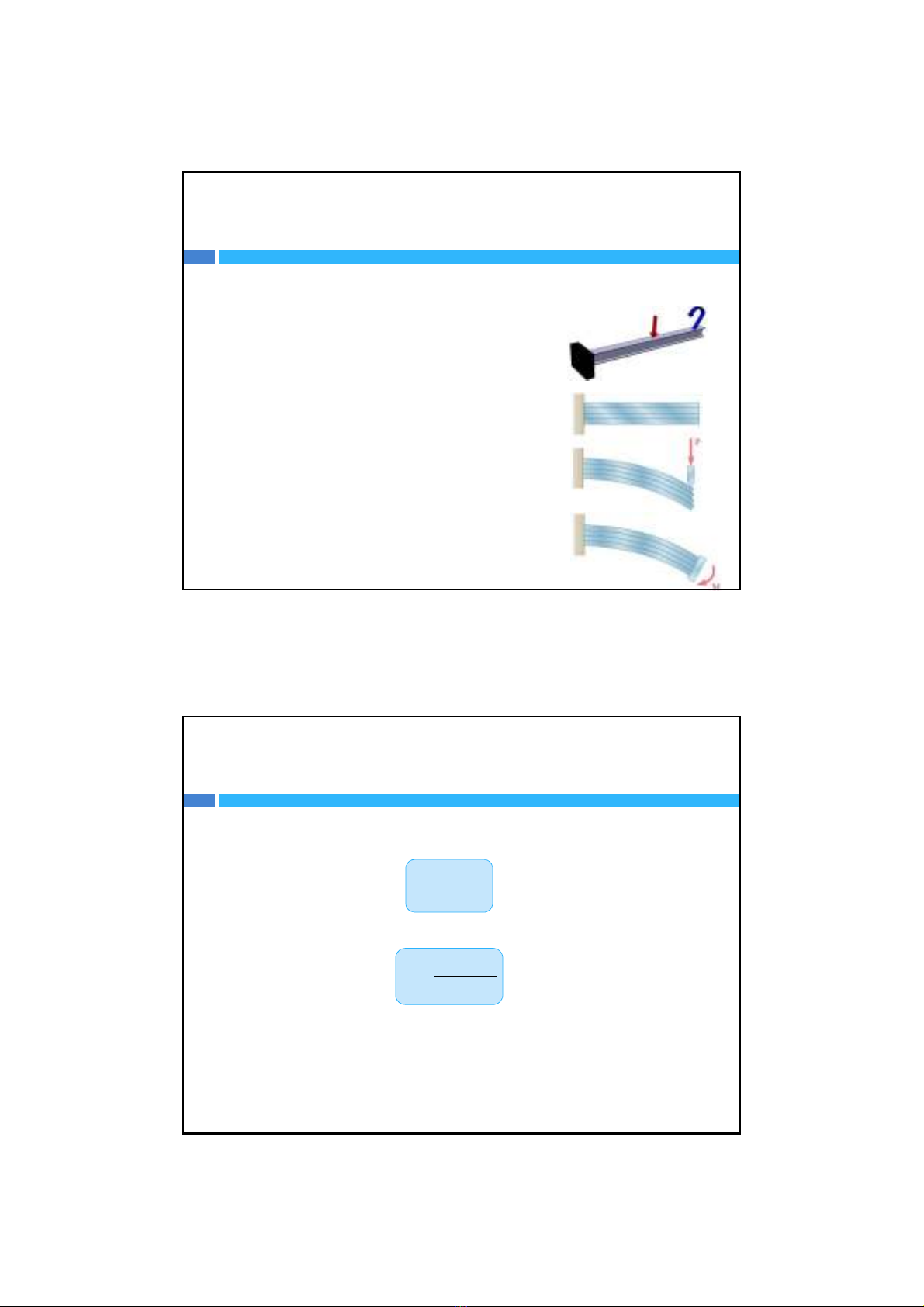
Mô‐men uốngâyraứng suất pháp làm đứtgãyvật
liệu. Lựccắtgâyraứng suấttiếp làm tách lớpcác
thớvậtliệu
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Ứng suấtphápzphân bốtrên mặtcắt ngang do Mxgây ra nên công thức
tính ứng suất pháp zgiống trong trường hợp thanh chịuuốnthuầntúy
x
z
x
My
J
Ứng suấttiếpzy do lựccắtQygâyrađượctínhbằng công thức
().
.( )
x
y
zy
x
SyQ
J
by
Moment tĩnh củaphầndiện tích tính từlớpbiên
ngoài cùng đế điểmmuốntínhứng suấttiếp(không
chứatrục trung hòa) đốivớitrục trung hòa.
Chiềurộng củamặtcắtngangđi qua điểmmuốntính
ứng suấttiếp và song song vớitrục trung hòa.
() ():
x
Sy fy
() ():by f y
Với:
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 9
11/13/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Công thứctínhứng suấttiếpchomộtsốmặtcắt thông thường
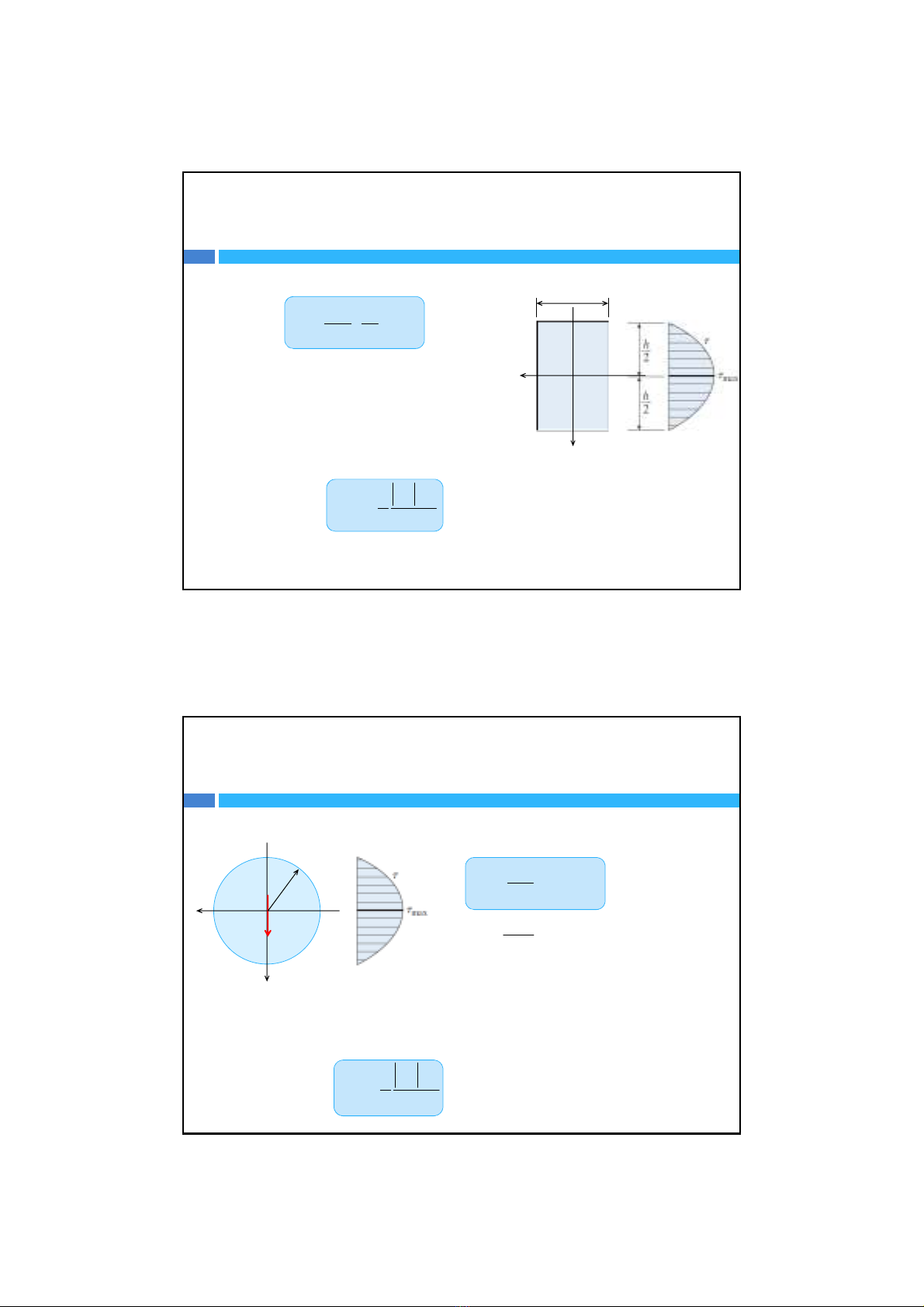
1. Mặtcắthìnhchữnhật
Công thứctínhứng suấttiếpzy
().
.( )
x
y
zy
x
SyQ
J
by
y
Q
x
y
z
Với: Qylà nộilựclựccắt
3
12
x
bh
J
()by b
:mô‐men quán tính hình chữnhật
:bềrộng mặtcắttheotọađộ y
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Mô‐men tĩnh đốivớitrụcx
x
C
y
y
C
2
h
2
h
b()
x
CC
Sy y A
/2 2
24
C
hyhy
yy

Với:
yC:tọađộ trọng tâm hình C theo tọađộ y
AC:diệntíchcủahìnhCtheotọađộ y
2
C
h
A
by




2
2
2
() 42 24
x
hy h bh
Sy b y y





Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 9
11/13/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Ta đượccôngthứctínhứng suấttiếpcủamặtcắthìnhchữnhật
2
2
3
6
4
y
zy
Qhy
bh




Ta thấycôngthứctínhứng suấttiếplàhàm
bậchaitheoy,ứng suấttiếpđạtgiátrịcực
đạikhiy=0 (lớp trung hòa)
Ta có công thứctínhứng suấttiếplớnnhấttrênmặtcắtngang:
max
max
3
2
y
Q
bh
x
y
b
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
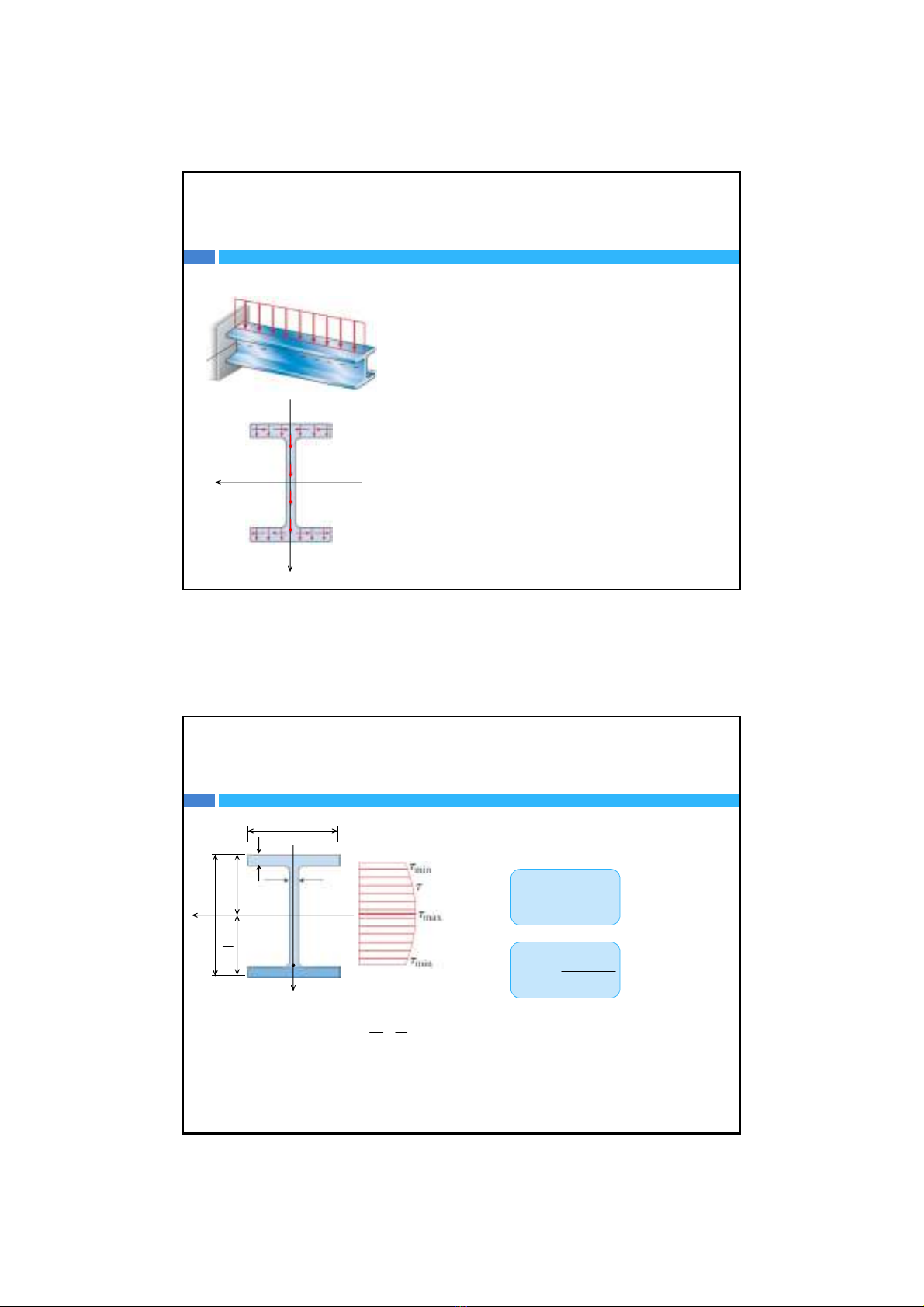
2. Mặtcắthìnhtròn
4
4
x
R
J
:mô‐men quán tính hình tròn

22
3
y
zy
x
Q
R
y
J

max
max 2
4
3
y
Q
R

Ta đượccôngthứctínhứng suấttiếp
x
y
y
Q
R
Ta có công thứctínhứng suấttiếplớnnhấttrênmặtcắtngang:
Ta thấycôngthứctínhứng suấttiếplà
hàm bậchaitheoy,ứng suấttiếpđạtgiá
trịcựcđạikhiy=0 (lớp trung hòa)
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 9
11/13/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
3. Mặtcắtngangđịnh hình
Phân bốứng suấttiếptrongmặtcắtđịnh hình
phứctạphơnsovớimặtcắthìnhchữnhật.
Ứng suấttiếptheophương ngang zx nhỏhơnrất
nhiềusovớiphương đứng zy do đótachỉxét
ứng suấttiếplớnnhấtzy,bỏqua ứng suấttiếp
zx.
Cách tìm ứng suấtcũng giống nhưcách tính ứng
suấttiếptrongmặtcắtchữnhật.
x
y
z
y
z
x
Thông thường sửdụng các dạng mặtcắtđịnh
hình có sẵntheotiêuchuẩnnênđể biếtcác
thông sốJx,W
x,S
xta tra bảng.
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
Công thứctínhứng suấttiếplớnnhấtvà
nhỏnhấttrongmặtcắtđịnh hình
max
yx
x
QS
Jd
min
D
yx
x
QS
Jd
Với
x
y
t
2
h
2
h
h
b
d
D
2
22
D
xx
dh
SS t




Là mô‐men tĩnh tạiđiểmD
Để biết các giá trịSx,J
x,d,h,ttrabảng vớimặtcắtđịnh hình tương ứng
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 9
11/13/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
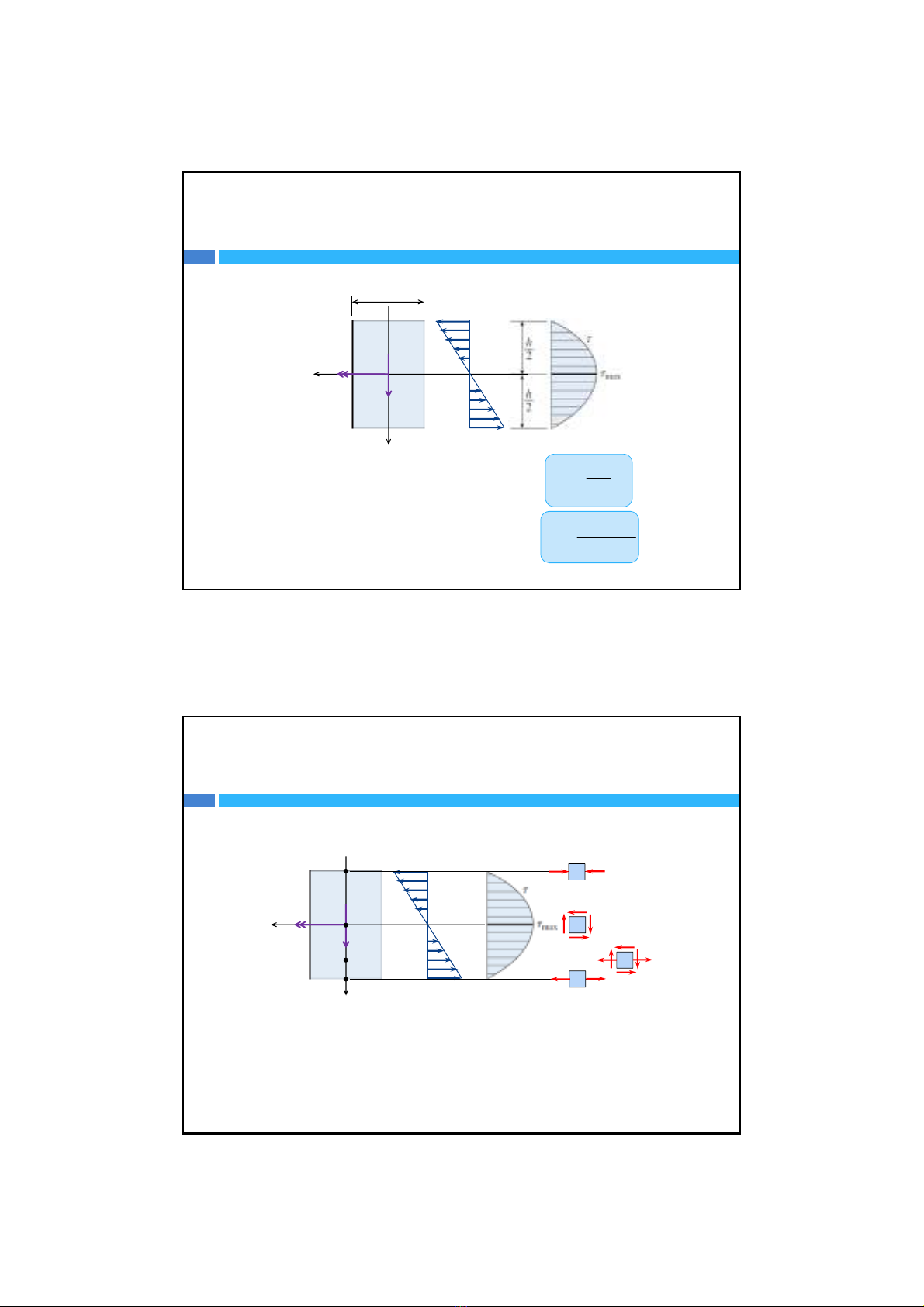
Trạng thái ứng suấtcácđiểmtrêntiếtdiện
Công thứctínhứng suấttiếpdolựccắtQ
y
().
.( )
x
y
zy
x
SyQ
J
by
x
y
b
x
M
y
Q
,maxn
,maxk
Công thứctínhứng pháp do mô‐men Mxgây ra x
z
x
My
J
CHƯƠNG 5 Tính bềncácbàitoánthuộcdạng thanh
3. Tính bềncácbàitoánthuộcdạng thanh
x
y
x
M
,maxn
,maxk
y
Q
O
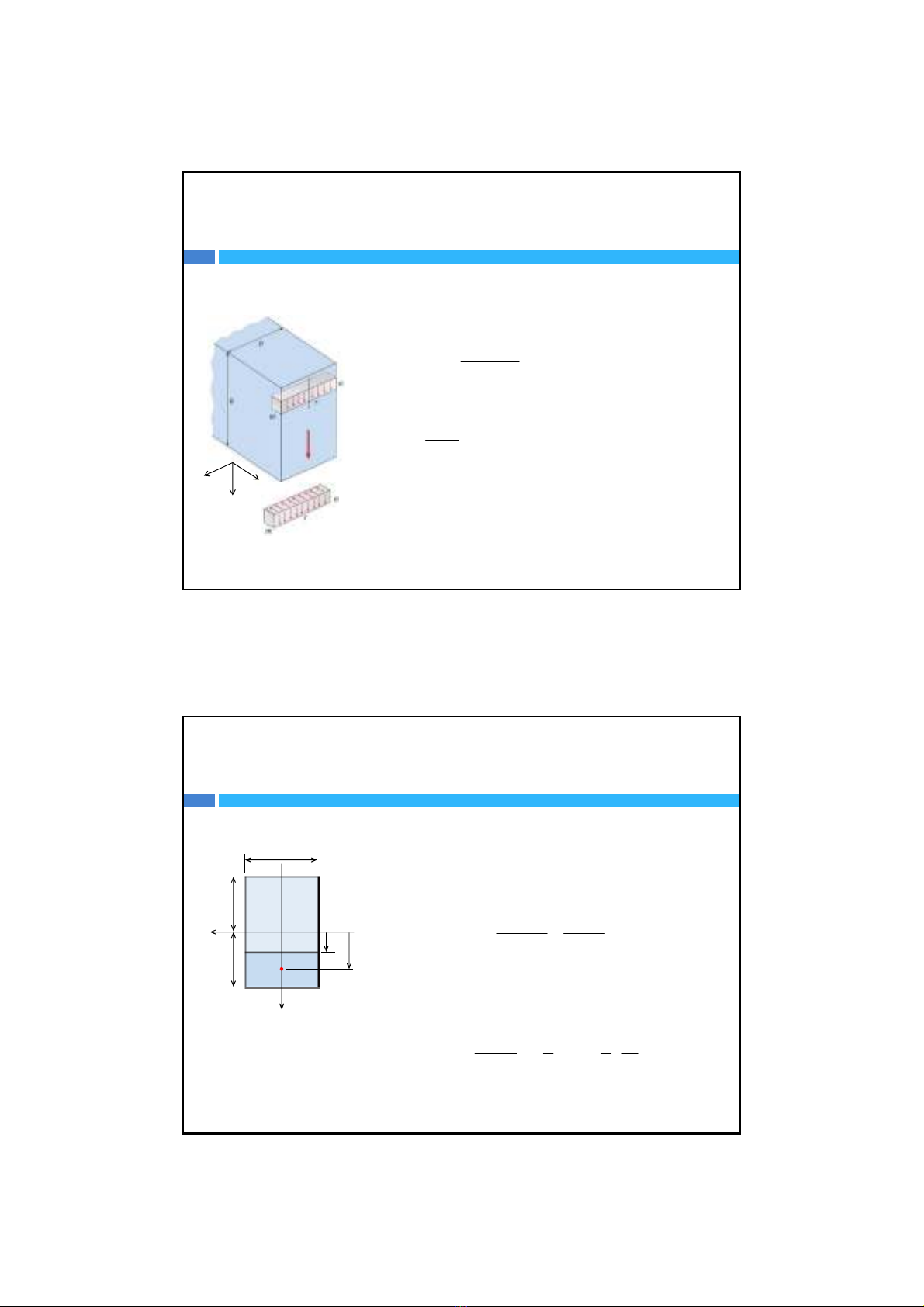
Hai thành phầnứng suấtđềulàhàmphụthuộcvàotọađộ y, vì thếcác
điểmcónhững điểmcùngtọađộ ysẽcó giá trịcác thành phầnứng suất
nhưnhau.
•TạiđiểmBvàHgọilàlớpbiên,chỉchịumột thành phầnứng suấtpháp
znên những điểmnàyởtrạng thái ứng suấtđơn.
B
H
D
H
B
O
D
•TạiđiểmOgọilàlớp trung hòa,chỉchịuứng suấttiếpzy nên những
điểmnàyởtrạng thái ứng suấttrượtthuầntúy.
•TạiđiểmDgọilàlớp trung gian,chịucảứng suất pháp zvà ứng suất
tiếpzy nên những điểmnàyởtrạng thái ứng suấtphẳng đặcbiệt.