
Economics 20 - Prof. Anderson 1
Dựbáo sửdụng mô hình chuỗithời
gian
(Time Series Models for Forecasting)
Hồiqui vớibiếntrễ
Regression with distributed lags
NguyễnNgọcAnh
Trung tâm Nghiên cứu Chính sách và Phát triển
NguyễnViệtCường
ĐạihọcKinhtếQuốcdân

Economics 20 - Prof. Anderson 2
Giớithiệu
Chúng ta ởtrong các bài trước, xem xét mô hình hồi qui,
sửdụng cho cảdữliệu chéo, lẫndữliệuchuỗithờigian.
Tuy nhiên, chúng ta ởđây lạithường quan tâm đếnnhững
biếnsốthay đổitheothời gian, chứkhông phảilànhững
biến thay đổi theo các cá nhân
Mô hình hồi qui tĩnh cho ta biếtquanhệgiữa các chuỗi
thời gian.
Ởđây, tác động củamộtbiếnX lênmộtbiếnY đượcgiả
thiếtlàchỉcó tác động trong cùng thờikỳ.

Economics 20 - Prof. Anderson 3
Mô hình động
Tác động mang tính động (Dynamic effects)
Chính sách cầncóthờigianmớicótácdụng
Mứcđộ cũng nhưtính chấtcủatácđộng có thể
thay đổitheothờigian
Tác động thường xuyên (Permanent) và tác
động tạmthời (Temporary effects.)
Economics 20 - Prof. Anderson 4
Trongkinhtếhọcvĩmô
Tác động củatiềntệM đốivới Y (GDP) trong
ngắnhạncóthểkhác vớitrongdàihạn
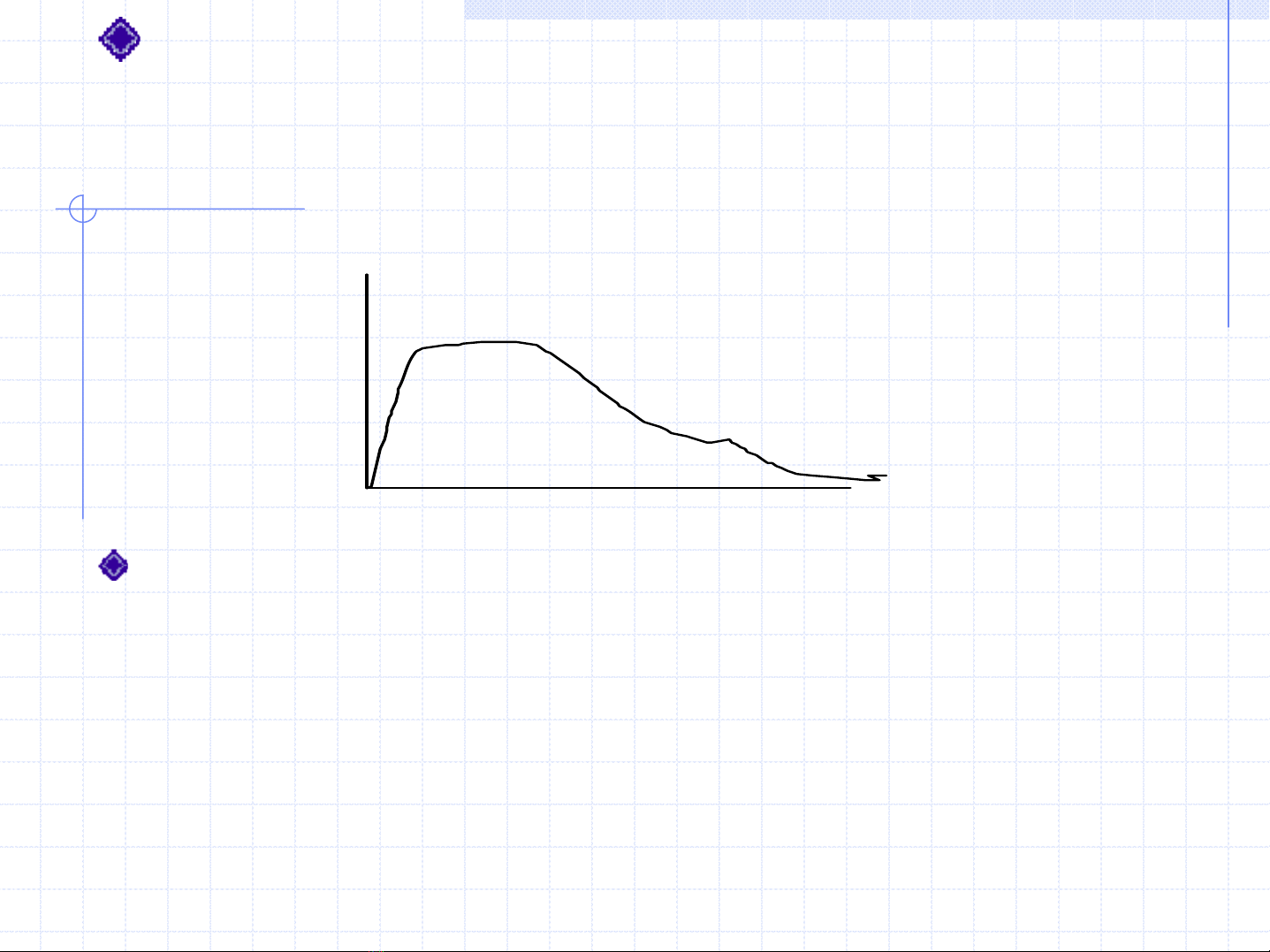
Ngườitathường gọilàhàmphảnứng (impulse response
function)
Tăng cung tiền trong mộtnămởnămthứ
Sau đósẽquay trởlạibìnhthường, không tăng M
nữa
ĐiềugìsẽxảyravớiY
time
Y

Economics 20 - Prof. Anderson 5
Phân bổtrễ(Distributed Lag)
Tác động được phân bổtheo thờigian
(Effect is distributed through time)
Hàm tiêu dùng : Tác động của thu nhậpcũng
thay đổitheothờigian
Tác động củathuếthu nhậpđốivới GDP sẽcó
độ trễ
Tác động của chính sách tiềntệvớiSX cũng
qua thờigian
yt= α+ β0xt+ β1xt-1 + β2xt-2 + et
it
t
ix
yE
−
=
δ
δ
β
)(


























