Thuy t liên k t hóa tr ế ế ị
Ph c ch t đc hình thành nh liên k t ứ ấ ượ ờ ế
c ng hóa tr cho - nh n gi a ộ ị ậ ữ các AO t ự
do c aủ ch t t o ph c và ấ ạ ứ các c p e ch a ặ ư
liên k t c aế ủ ph i t ố ử
S ph i trí và c u hình c a ph c ch t ố ố ấ ủ ứ ấ
ph thu c vào s AO tham gia t o liên ụ ộ ố ạ
k t và tr ng thái lai hĩa c a nguyên t / ế ạ ủ ử
ion trung tâm.
Thuy t liên k t hóa tr ế ế ị
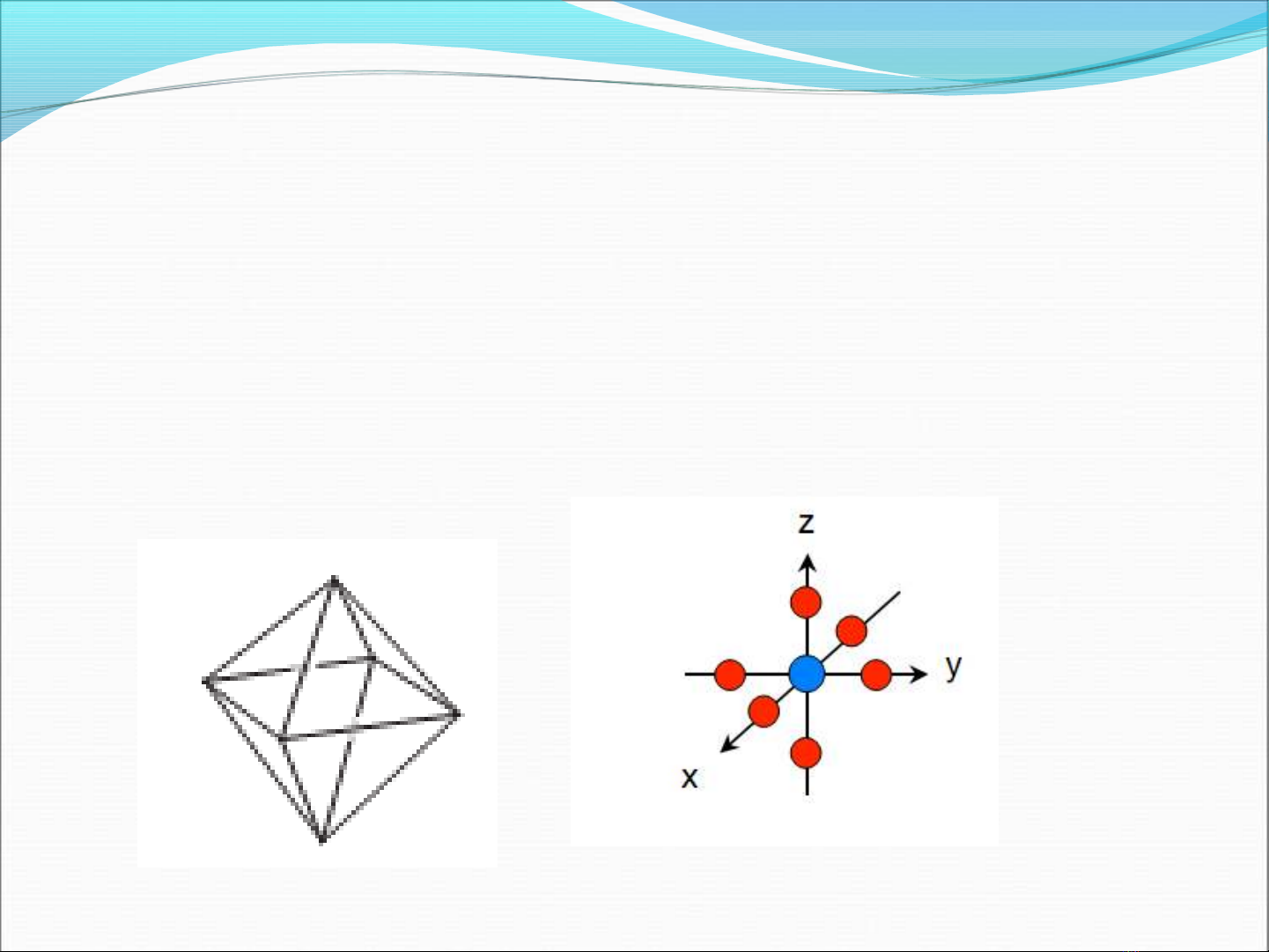
Ph c hexafloridocobaltat(III) ứ
C u hình : baùt dieänấ
Tính ch t t : Thu n tấ ừ ậ ừ
M u s c ion ph c: xanh lô ầ ắ ứ
Thuy t liên k t hóa tr ế ế ị
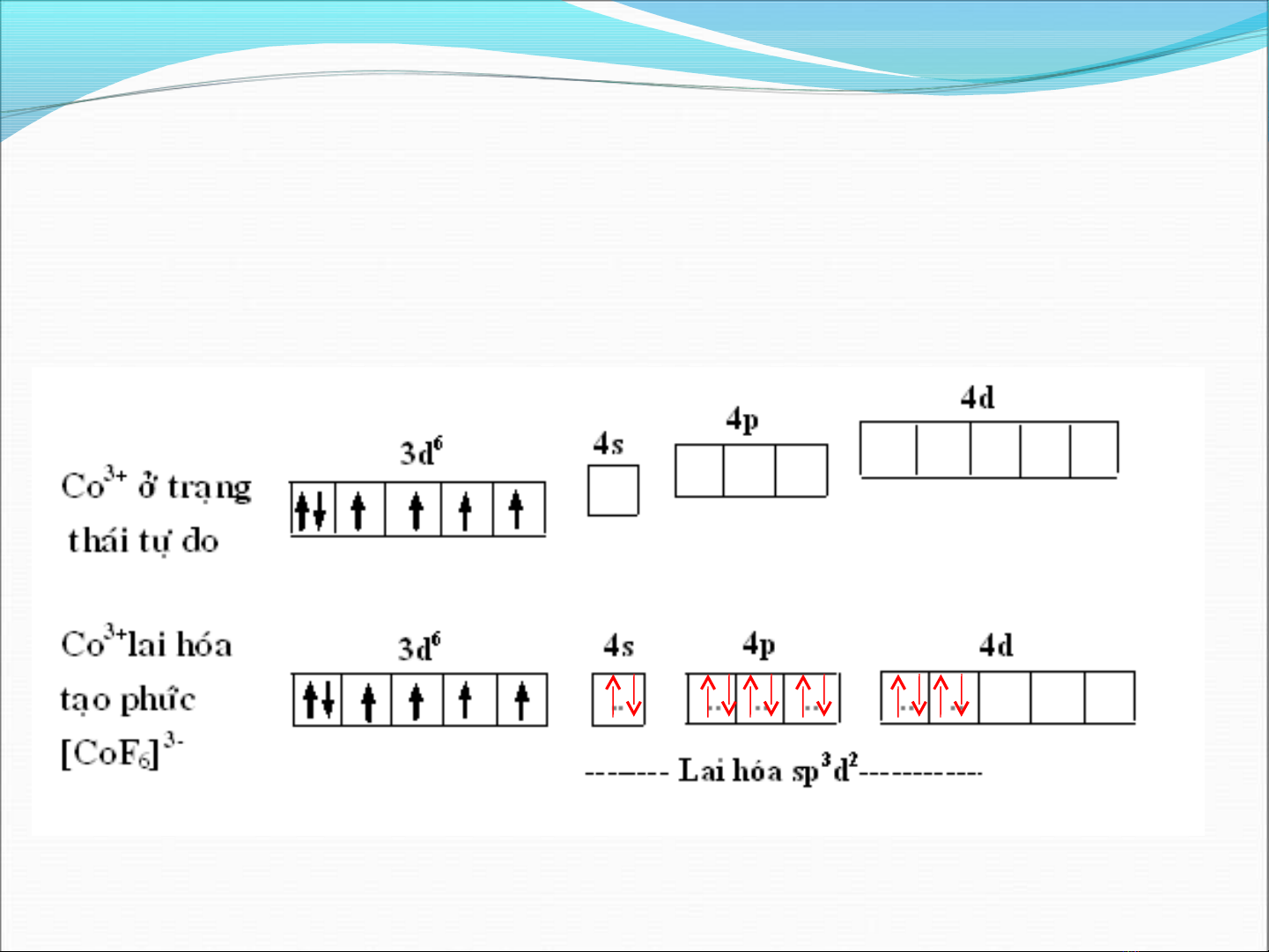
Ph c hexafloridocobaltat(III)ứ
Gi i thích theo thuy t liên k t hóa tr :ả ế ế ị
Phức orbital ngoài
Phức [CoF6]3- có nhiều e độc thân phức spin cao
Thuy t liên k t hóa trế ế ị
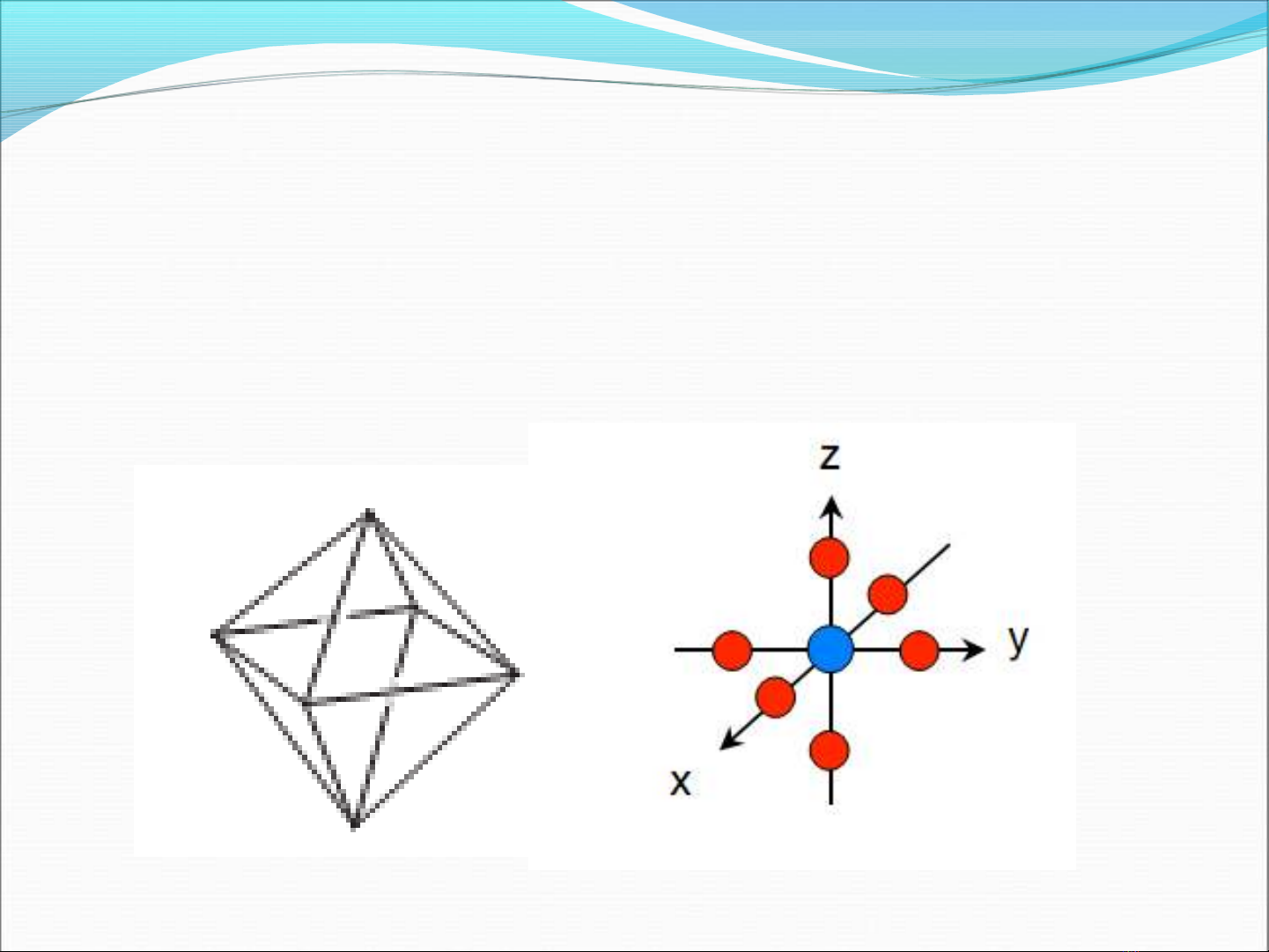
Ph c hexaammincobalt(III) ứ
C u hình: baùt dieänấ
Tính ch t t : Ngh ch t ấ ừ ị ừ
M u s c ion ph c: maøu vaøngầ ắ ứ
