Hàm dạng Ma trận độ cứng Véc-tơ lực nút tương đương
NỘI DUNG CHÍNH
1Hàm dạng
Hàm chuyển vị cho phần tử tuyến tính
Một quy trình xác định hàm dạng
Hàm dạng của một số phần tử thanh tuyến tính
2Ma trận độ cứng
Quy trình chung
Phần tử thanh chịu kéo/nén đúng tâm
Phần tử thanh chịu uốn ngang phẳng, nút cứng hai đầu
3Véc-tơ lực nút tương đương
Quy trình chung
Phần tử thanh chịu kéo/nén và uốn
Hàm dạng Ma trận độ cứng Véc-tơ lực nút tương đương
NỘI DUNG CHÍNH
1Hàm dạng
Hàm chuyển vị cho phần tử tuyến tính
Một quy trình xác định hàm dạng
Hàm dạng của một số phần tử thanh tuyến tính
2Ma trận độ cứng
Quy trình chung
Phần tử thanh chịu kéo/nén đúng tâm
Phần tử thanh chịu uốn ngang phẳng, nút cứng hai đầu
3Véc-tơ lực nút tương đương
Quy trình chung
Phần tử thanh chịu kéo/nén và uốn
Hàm dạng Ma trận độ cứng Véc-tơ lực nút tương đương
Hàm chuyển vị cho phần tử tuyến tính
• •
• •
•
• •
••
•
••
•
•
••
•• •
•
•
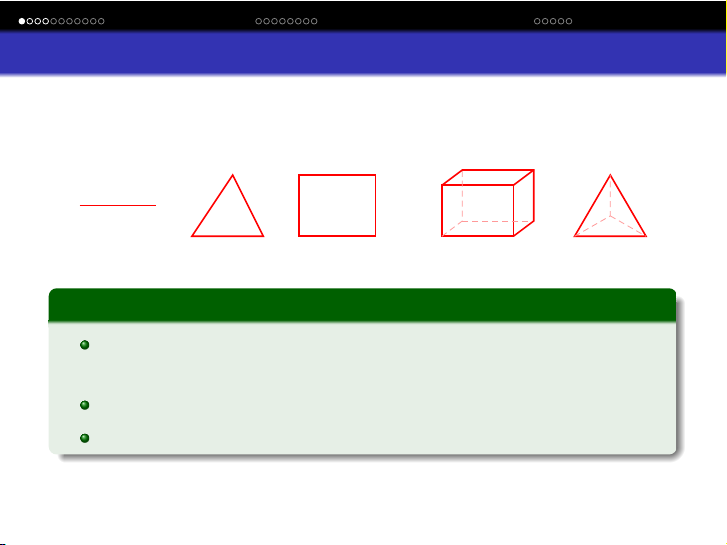
Phần tử tuyến tính
Khi chỉ có các điểm nút đặt ở đỉnh của phần tử ⇒phần tử
"tuyến tính"∗
Đơn giản cho việc thiết lập công thức các ma trận phần tử
Trong các tính toán yêu cầu độ chính xác cao, ít dùng!
Hàm dạng Ma trận độ cứng Véc-tơ lực nút tương đương
Hàm chuyển vị cho phần tử tuyến tính
Hàm chuyển vị
Thường được chọn ở dạng đa thức
Trường hợp phần tử tuyến tính, chọn các hàm chuyển vị là
các đa thức có số thành phần đúng bằng số chuyển vị tại
nút của phần tử .
Với phần tử thanh tuyến tính, bài toán 1 chiều:
u(x) = a1+a2x
Với phần tử 2D tam giác tuyến tính:
ux(x, y) = a1+a2x+a3y
uy(x, y) = a4+a5x+a6y