Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
CHƯƠNG 07:
PHƯƠNG PHÁP ĐỒ THỊ ĐỂ GIẢI BÀI
TOÁN TỐI ƯU HÓA CÓ 2 THAM BIẾN
Thời lượng: 3 tiết
2
Đặt vấn đề
Trong rất nhiều bài toán thiết kế, kỹ thuật phức tạp, số lượng các
hàm ràng buộc (bất đẳng thức) là rất lớn, tuy nhiên hàm mục tiêu
và các ràng buộc chỉ có 2 tham biến. Với những bài toán này, nhiều
khi áp dụng phương pháp đồ thị sẽ đem lại hiệu quả tốt, đồng thời
đưa ra một lời giải trực quan và dễ hiểu. Hơn nữa, trong 1 số
trường hợp khi lời giải cần tìm phải là số nguyên, thì phương pháp
đồ thị trong trường hợp này lại giúp tìm ra kết quả dễ dàng mà
không cần sử dụng những kỹ thuật phức tạp khác.
3 bước Cơ bản của phương pháp này là:
-Vẽ đồ thị các hàm ràng buộc
-Xác định miền lời giải hợp lệ (vùng diện tích được giới hạn bởi
các đường cong ràng buộc)
-Vẽ các đường cong đồng mức của hàm mục tiêu để xác định cực
trị ở trong miền hợp lệ
Chú ý: Đi theo hướng của Gradient đến điểm cực trị nhưng phải
trong khuôn khổ miền hợp lệ
3
Phương pháp đồ thị
Cực đại hóa hàm số sau:
1 2 1 2
, 400 600 maxf x x x x
Với các ràng buộc:
1 2 1 2
1 2 1 2
16; 1; 1; 0; 0
28 14 14 24
x x x x
x x x x
Bước 1: Kẻ hệ trục tọa độ x1x2
Nhìn vào các ràng buộc để dự đoán một cách tương đối về
khoảng giá trị của các tham biến. Ví dụ ở đây ta có thể lấy
[0;25].
Trong nhiều trường hợp khoảng giá trị trên các trục chỉ có thể
xác định sau khi vẽ các đồ thị.
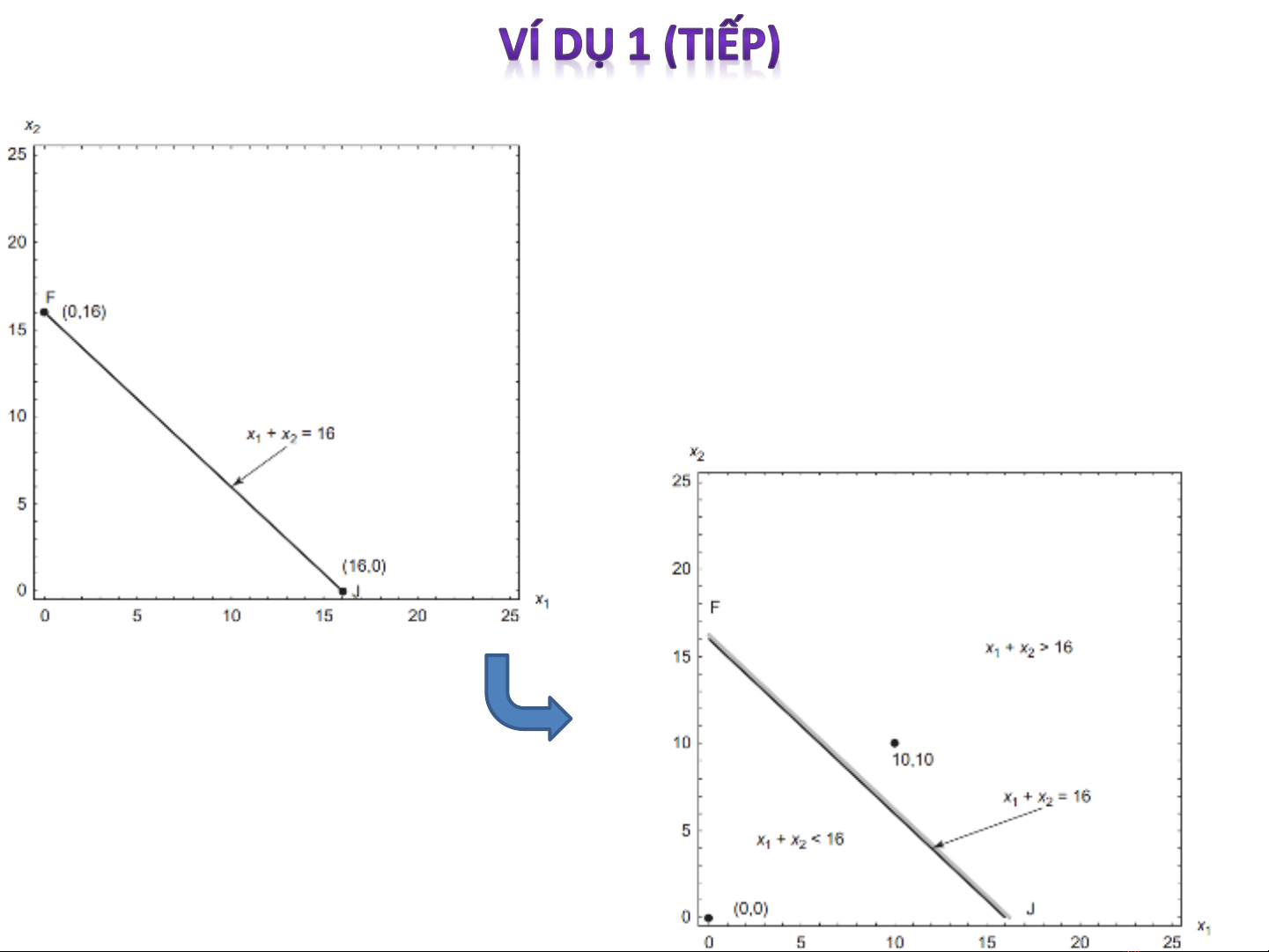
Bước 2: Vẽ các đường ràng buộc bất đẳng thức
Xét ràng buộc đầu tiên, ta bỏ dấu bất đẳng thức ≤ để vẽ đồ thị
đường:
12
16 0xx
4
Bước 3: Phân định miền bất đằng
thức: Dựa vào tọa độ của 1 điểm
thuận tiện không nằm trên đường
cong ràng buộc thuộc 1 trong 2
miền. Từ đó xác định được dấu
của 2 miền 2 phía đường cong.
Không hợp lệ
Hợp lệ
5
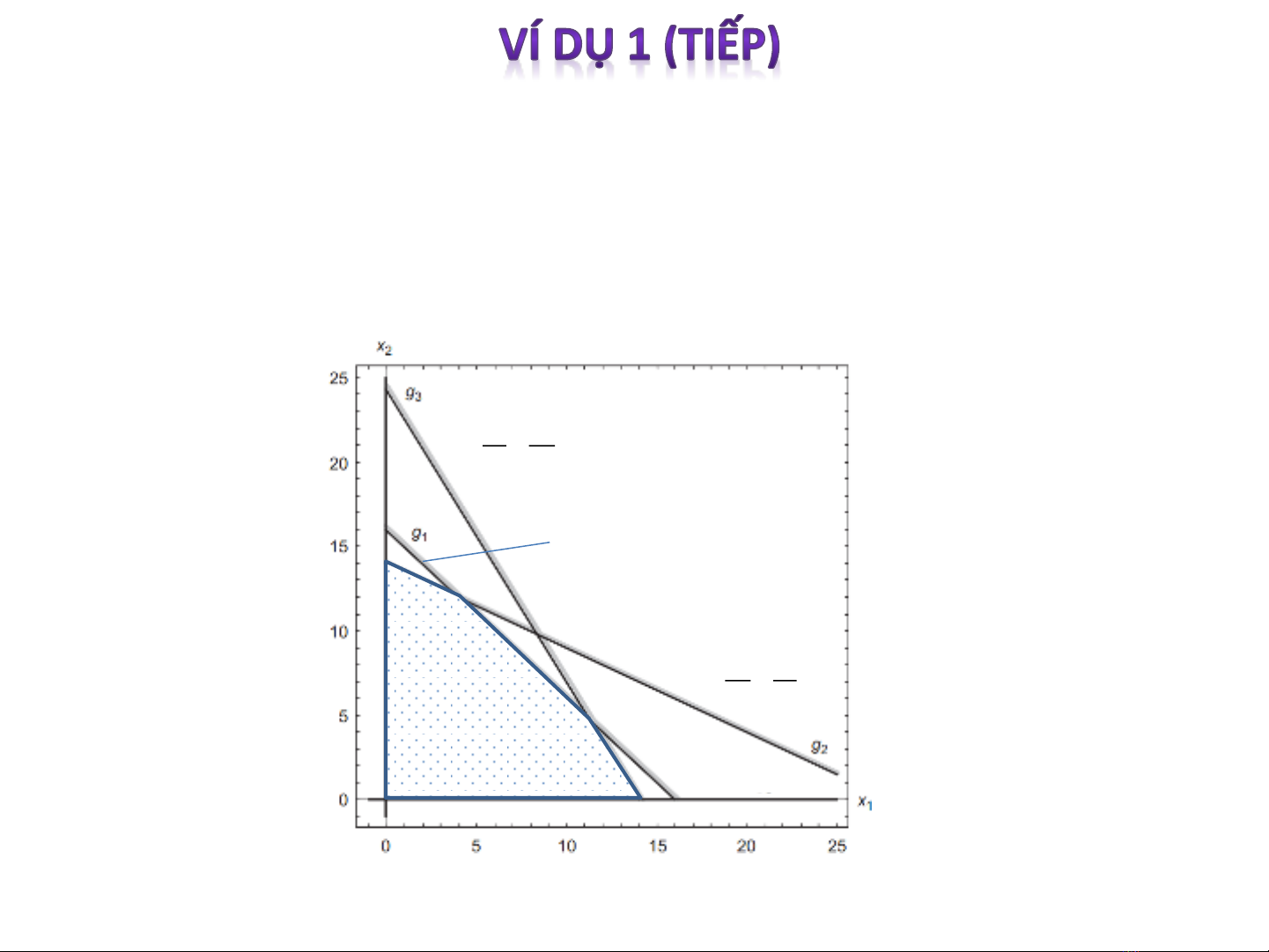
Bước 4: Vẽ các đường cong ràng buộc còn lại và xác định miền
hợp lệ: Làm tương tự bước 3 cho các đường cong ràng buộc
còn lại
A
B
J
H
C
12
21
28 14
xx
g
12
31
14 24
xx
g
520gx
410gx
1 1 2 16g x x
D
E
Miền
ABCDE
hợp lệ