Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
CHƯƠNG I:
NHỮNG KHÁI NIỆM CƠ BẢN
Thời lượng: 6 tiết (2 buổi)
2
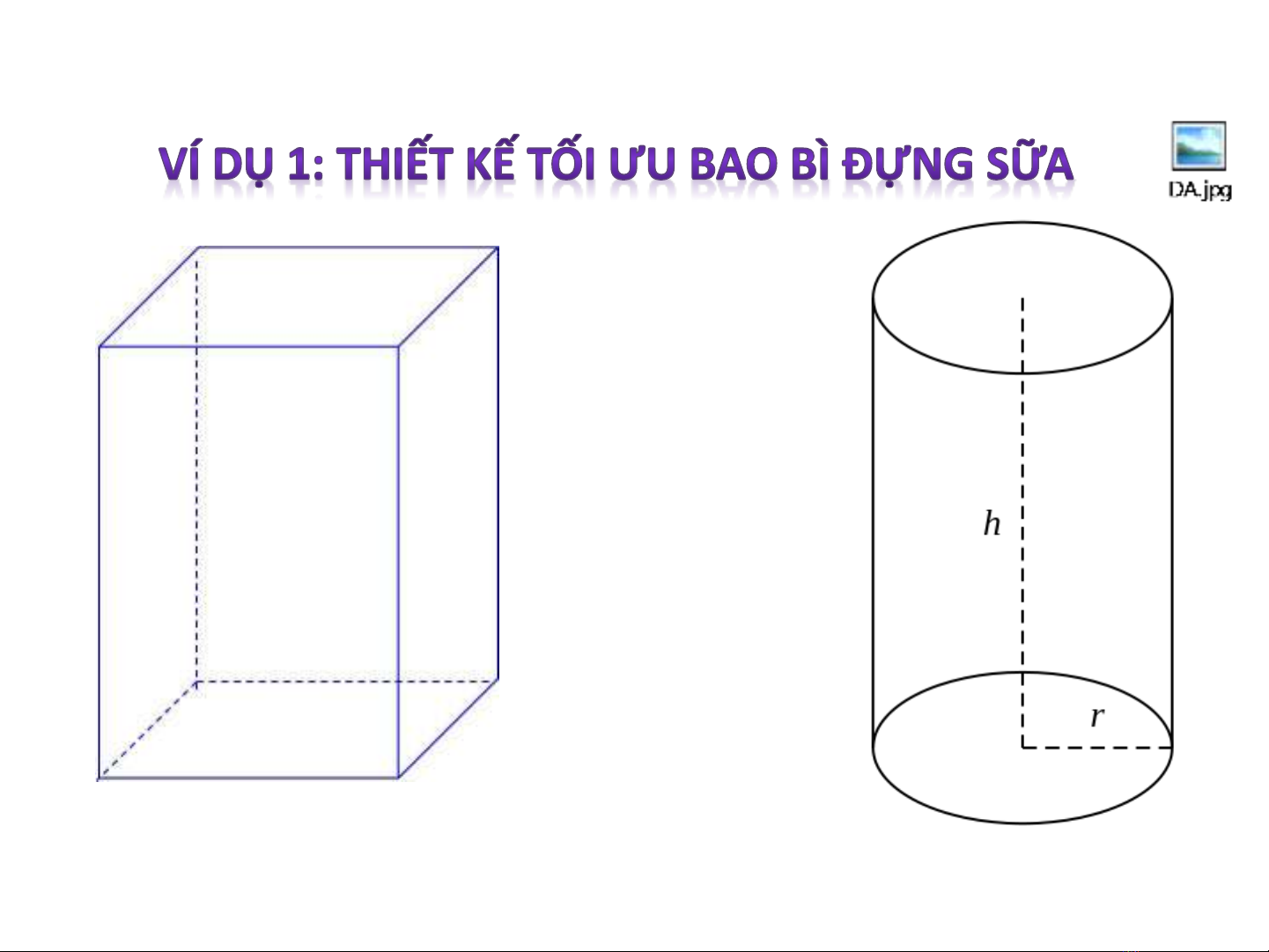
Các tình huống tối ưu hóa trong thiết kế Cơ khí
3
1 dm minVS
h
a
a
3
Các tình huống tối ưu hóa trong thiết kế Cơ khí
Cho dầm với mặt cắt hình tròn đặc với đường kính d, được
làm từ vật liệu có khối lượng riêng ρ. Chiều dài dầm là L.
Tìm đường kính d để khối lượng dầm là tối thiểu, biết tần số
dao động riêng thứ nhất của nó không được vượt quá giá trị
f
4
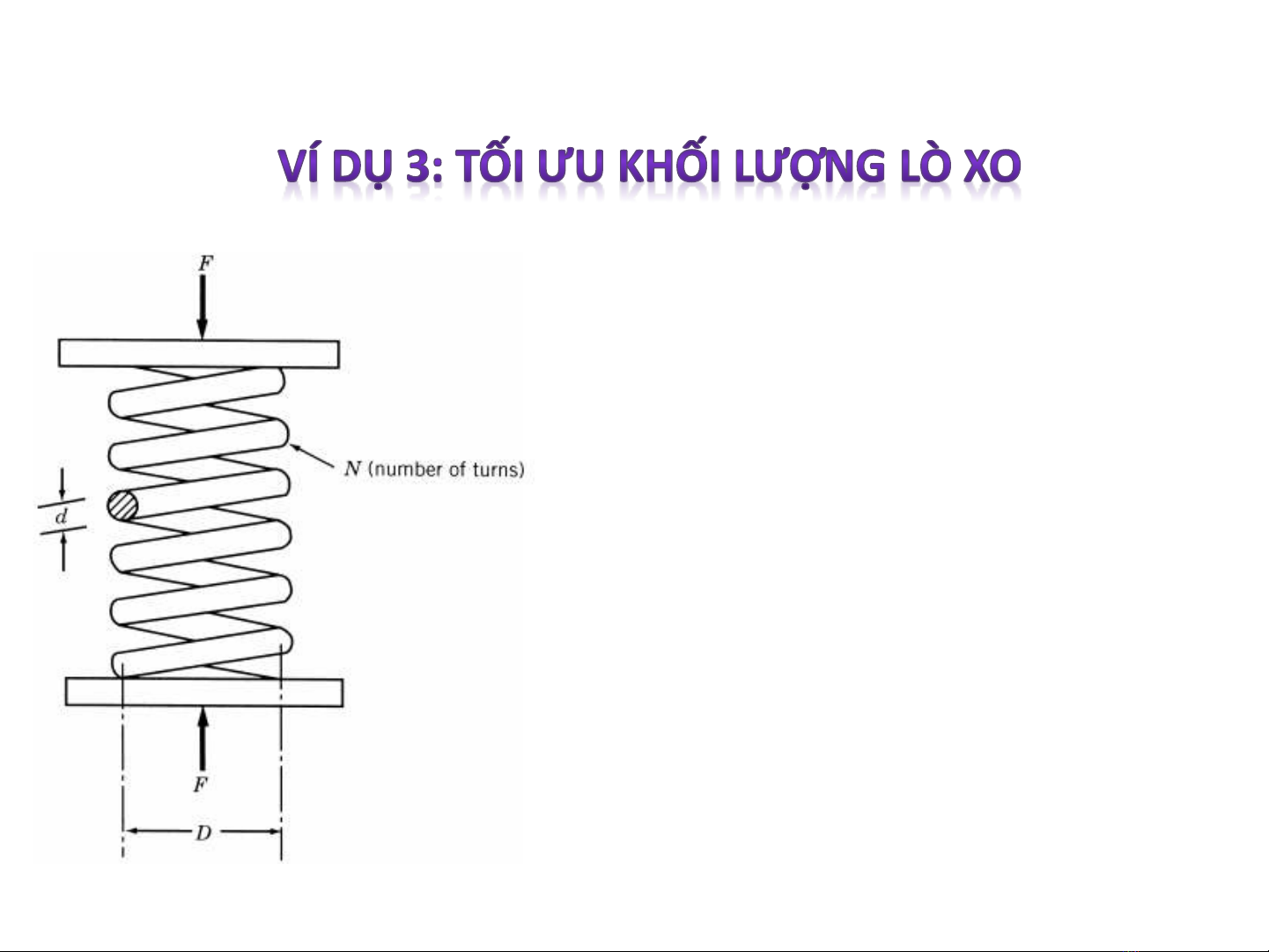
Các tình huống tối ưu hóa trong thiết kế Cơ khí
Tìm d, D, N để lò xo nhẹ nhất
mà vẫn đảm bảo các điều
kiện:
-Về độ cứng
-Về độ bền
-Về tần số dao động
5
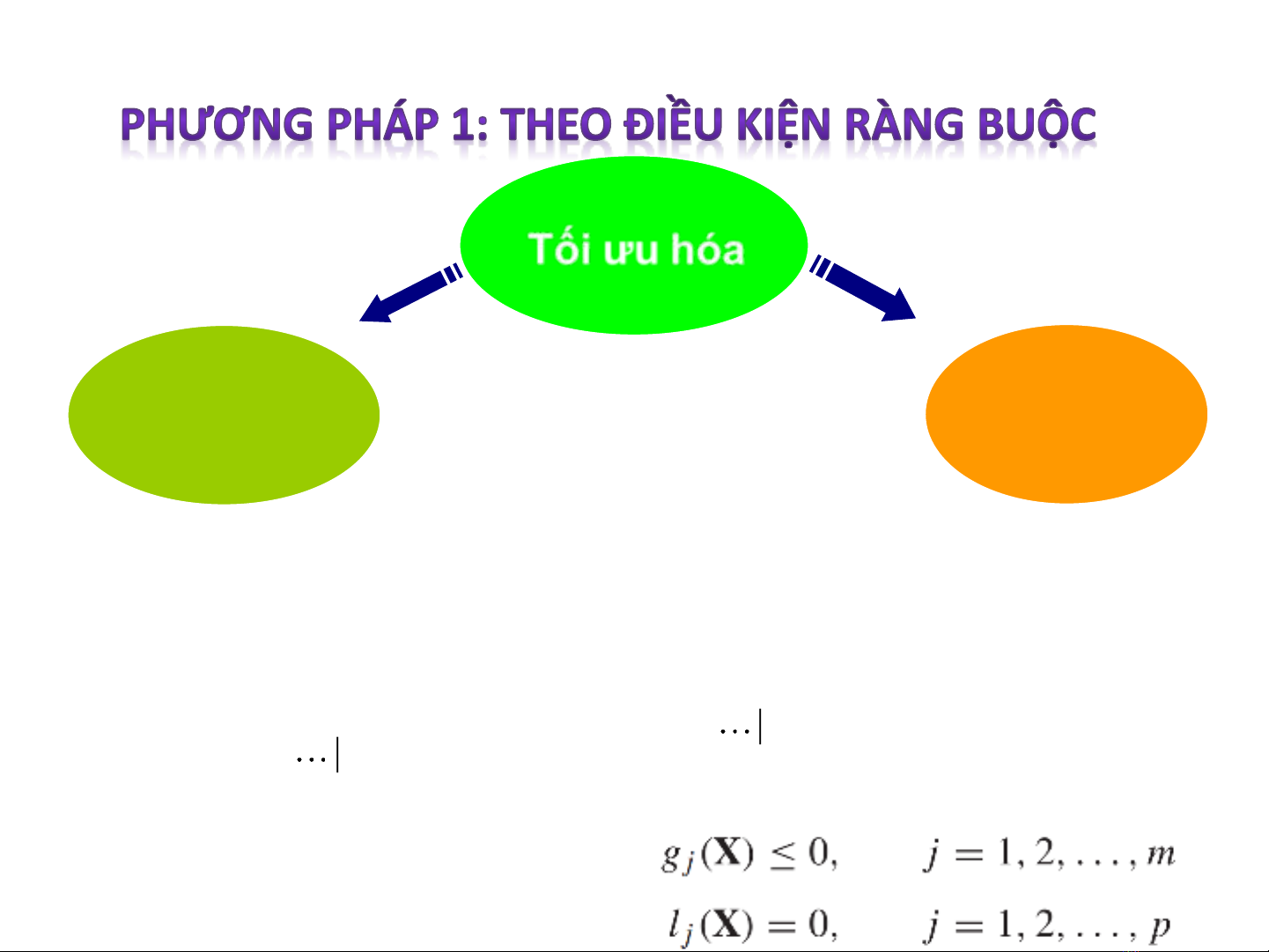
Phân dạng các vấn đề tối ưu hóa
Tối ưu hóa
Không ràng
buộc
Có ràng
buộc
Phát biểu của một vấn đề tối ưu hóa
1
2
n
x
x
x






X
Tìm
Để hàm f(X) nhỏ nhất
1
2
n
x
x
x






X
Tìm Để hàm f(X) nhỏ nhất
và phải thỏa mãn các
điều kiện ràng buộc