Bài giảng Tối ưu hóa và quy hoạch tuyến tính - Chương 2: Bài toán đối ngẫu

Chia sẻ: Hoamaudon | Ngày: | Loại File: PDF | Số trang:40

Thêm vào BST

Báo xấu

24
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Tối ưu hóa và quy hoạch tuyến tính - Chương 2: Bài toán đối ngẫu cung cấp cho người học những kiến thức như: Ý nghĩa và cách lập bài toán đối ngẫu; Giải bài toán đối ngẫu; Ứng dụng của bài toán đối ngẫu. Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Tối ưu hóa và quy hoạch tuyến tính - Chương 2: Bài toán đối ngẫu

Chương 2 BÀI TOÁN ĐỐI NGẪU 1
2 NỘI DUNG CHƯƠNG 2.1 Ý nghĩa và cách lập bài toán đối ngẫu 2.2 Giải bài toán đối ngẫu 2.3 Ứng dụng của bài toán đối ngẫu
2.1 Ý nghĩa và cách lập bài toán đối ngẫu  Xét bài toán sản xuất tối ưu: Z  2 x1  3 x2  4 x3  max 10x1  20 x2  30 x3  10000 20 x1  30 x2  30 x3  50000 (2.1.1) 20 x1  30 x2  40 x3  30000 x j  0, j  1, 2,3 Có một đối tác đặt vấn đề mua toàn bộ nguyên liệu của cty A. Hãy lập bài toán định giá mua ng/liệu rẻ nhất. 3
Ý nghĩa và cách lập bài toán đối ngẫu Gọi yi, i=1,2,3 là giá mua 1 đ/vị nguyên liệu đường, sữa, bột tương ứng. Z   10000 y1  50000 y2  30000 y3  min 10y1  20 y2  20 y3  2 20 y1  30 y2  30 y3  3 (2.1.1) 30 y1  30 y2  40 y3  4 yi  0, i  1, 2,3 Bài toán (2.1.1)’ gọi là BTĐN của (2.1.1). 4
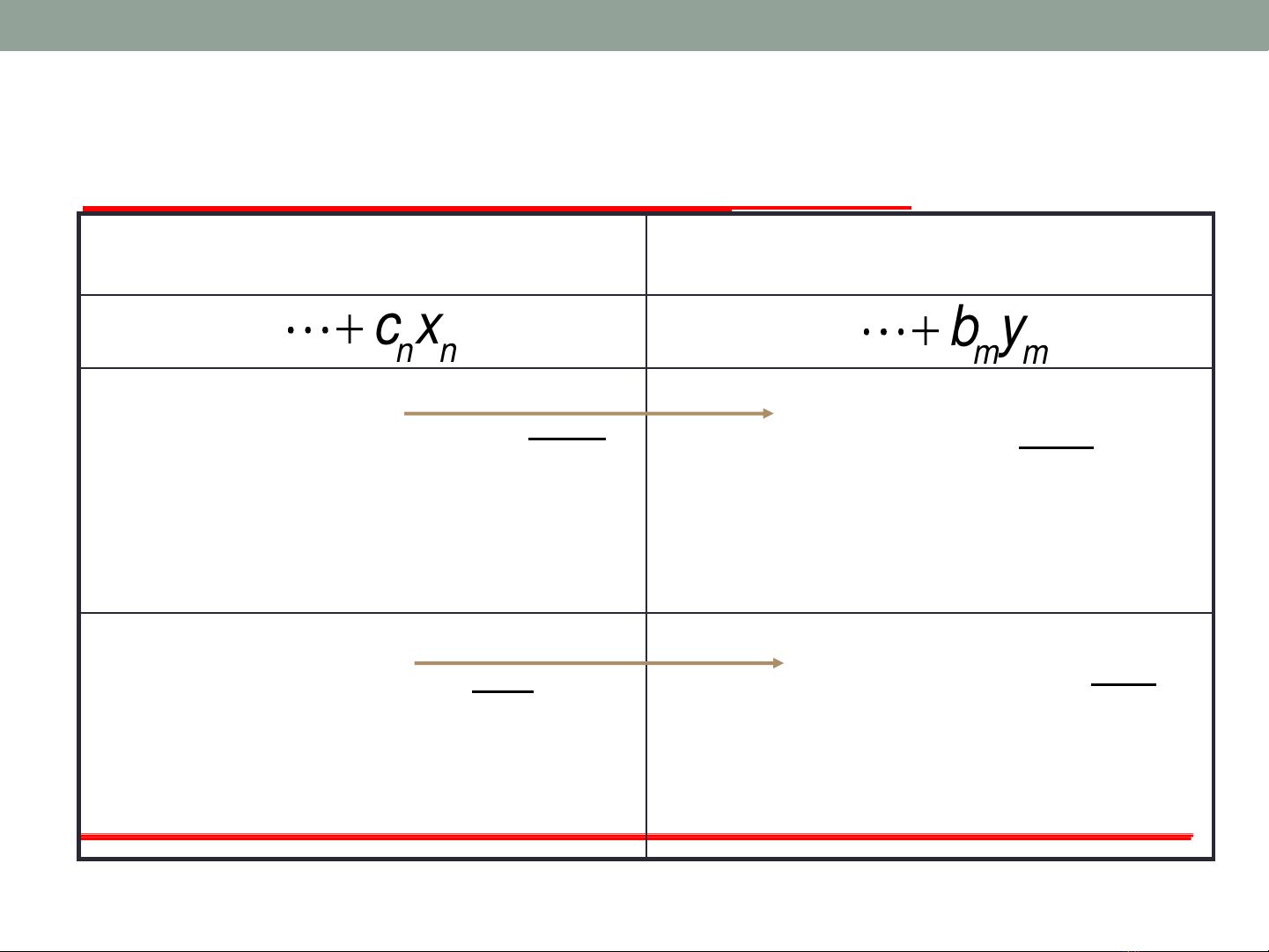
Lập bài toán đối ngẫu Bài toán xuất phát(ĐNgẫu) Bài toán đối ngẫu (X.phát) Z  c1x1   cn xn  max Z  b1y1   bmym  min   RBD ngược dấu RBC n   0  aij x j   bi ,(i  1, m) yi   0  ,(i  1, m) j 1     tùy ý  RBC cùng dấu RBD xj    0  m x j   0  ,( j  1, n)  a y    cj ,( j  1, n)  tùy ý  ij i     i 1    5
6 Lập bài toán đối ngẫu Ví dụ 2.1.1a Xét bài toán QHTT BTDN Z  2 x1  x2  8 x3  max Z   28 y1  10 y2  15 y3  min 7 x1  4 x2  2 x3  28 7 y1  3 y2  2 y3  2 3 x1  x2  3 x3  10 4 y1  y2  3 y3  1 2 x1  3 x2  x3  15 2 y1  3 y2  y3  8 y1  0, y3  0 x j  0, j  1,3
7 Lập bài toán đối ngẫu b) BTĐN Z  x1  2 x2  3x3  min Z   2 y1  3 y2  4 y3  5 y4  max 2x1  2 x2  x3  2 2 y1  y2  y3  2 y4  1 x1  x2  4 x3  3 2 y1  y2  2 y3 2  x1  2 x2 4  y1  4 y2  y4  3 2 x1  x3  5 y1 , y3  0; y2 , y4  0 x1 , x2  0
8 Cặp ràng buộc đối ngẫu  Trong một cặp bài toán đối ngẫu, ta gọi hai ràng buộc bất đẳng thức trong hai bài toán cùng tương ứng với một chỉ số(quy định dấu bất đẳng thức lẫn nhau) là một cặp ràng buộc đối ngẫu.
9 Cặp ràng buộc đối ngẫu Ví dụ 2.1.2 Ở ví dụ 2.1.1a thì có 5 cặp ràng buộc đối ngẫu sau: x1  0  7 y1  3 y2  2 y3  2 x2  0  4 y1  y2  3 y3  1 x3  0  2 y1  3 y2  y3  8 7 x1  4 x2  2 x3  28  y1  0 2 x1  3 x2  x3  15  y3  0
10 Các định lý đối ngẫu Định lý đối ngẫu yếu: Nếu x*là phương án tùy ý của bài toán gốc (P) và y* là phương án tùy ý của bài toán đối ngẫu (D) thì Z(x*) ≤ Z’(y*). Hệ quả 1: Nếu một trong hai bài toán (của cặp bài toán đối ngẫu) có phương án tối ưu thì bài toán còn lại cũng có phương án tối ưu.
11 Các định lý đối ngẫu Hệ quả 2: Nếu x0 là PA của (P)    x là PATƯ của (P) 0 y0 là PA của (D)      y0 là PATƯ của (D) và Z(x ) = Z’(y )  0 0
12 Các định lý đối ngẫu Định lý đối ngẫu mạnh: Nếu x* là PATƯ của (P)    Z ( x * )  Z ( y*) y* là PATƯ của (D) 
13 Các định lý đối ngẫu Định lý độ lệch bù yếu: Điều kiện cần và đủ để PA x0 của bài toán (P) và PA y0 của bài toán (D) là là 2 PA tối ưu là:  0 m    x j  aij yi  c j   0,( j  1, n)   i 1 0   n   0   aij x j  bi  yi  0,(i  1, m) 0  j 1 
14 Các định lý đối ngẫu Hoặc phát biểu tương đương: Đk cần và đủ để x0 và y0 là PATƯ của bài toán (P) và (D) tương ứng là trong từng cặp ràng buộc đối ngẫu của cặp bài toán đó: nếu một ràng buộc (của bài toán này) thỏa mãn với dấu bất đẳng thức thực sự (thỏa mãn lỏng) thì ràng buộc còn lại (của bài toán kia) phải thỏa mãn với dấu đẳng thức (thỏa mãn chặt), i.e.,
15 Các định lý đối ngẫu . - Neu x  0 hay x  0 thì a y  0 j 0 j 0 1j 1  a y  cj 0 mj m 0 - Neu a x + i1 1 +a x >(
16 2.2 Giải BTĐN khi biết PATƯ BT gốc Cho bt QHTT (P) và một PATƯ x0. Cần giải btdn (D) của (P)? Bước 1: Lập btđn (D) của (P) Bước 2: Lập hệ pt tối ưu cho biến bt (D). (dựa vào đlý độ lệch bù yếu) - Giải hệ này tìm nghiệm y0. Bước 3: Kết luận lời giải cho bt (D) - Nếu y0 thỏa các Rb còn lại của (D) thì nó là PATƯ cần tìm của (D).
17 2.2 Giải BTĐN khi biết PATƯ BT gốc Vi dụ 2.2.1: Z  3x1  4 x2  x3  min  3x1  2 x2  4 x3  15 2 x1  x2  5 x3  8 4 x1  2 x2  2 x3  10 (2.2.1) x1 , x2  0; x3  0 Có phương án tối ưu la x0=(7,0,-9) . Hãy lập và giải bài toán đối ngẫu của bài toán trên?
2.2 Giải BTĐN khi biết PATƯ BT gốc BTĐN của bt (2.2.1) là: Z  15y1  8y2  10y3  max 3y1  2y2  4y3  3 Z  3x1  4 x2  x3  min 2y1  y2  2y3  4  3x1  2 x2  4 x3 15  y1 4y1  5y2  2y3  1   2 x1  x2  5 x3 8   y2  y1, y2 , y3  0 4 x1  2 x2  2 x3 10  y  3  (2.2.1) x1 , x2  0; x3  0 18
19 2.2 Giải BTĐN khi biết PATƯ BT gốc Do x0=(7,0,-9) là PATƯ của bt (2.2.1) nên theo đlý đ.l.b.y ta có hệ: 3y1  2y2  4y3  3  y1  1/ 5   4y1  5y2  2y3  1   y2  0    y2  0  y3  9 / 10 Ta thấy y0=(1/5, 0, 9/10) thỏa các RB của btđn   12 nên nó là PATƯ của btdn và Zmax
20 2.3 Ứng dụng của bài toán đối ngẫu 2.3.1 Giải bt QHTT bằng bài toán đối ngẫu. 2.3.2 Kiểm chứng tính tối ưu của một PA. 2.3.3 Tìm tập PATƯ của một bài toán QHTT