
ÑIEÀU KHIEÅN THOÂNG MINH
(Baûn nhaùp)
2
TOÅNG QUAN
nÑieàu khieån thoâng thöôøng (conventional control)
nÑieàu khieån kinhñieån (classical control)
nÑieàu khieån hieänñaïi (modern control)
nÑieàu khieån toáiöu (optimal control)
nÑieàu khieån thích nghi (adaptive control)
nÑieàu khieån beàn vöõng (robust control)
nÑieàu khieån thoâng minh
nÑieàu khieån môø(fuzzy control)
nMaïng neural (neural network)
nGiaûi thuaät di truyeàn (gene algorithm)
3
Ñieàu khieån thoâng thöôøng
nÖu:
nCoùcô sôûtoaùn hoïc chaët cheõ
®Coùtheåduøng caùc coâng cuïtoaùn hoïcñeåphaân tích &
thieát keáheäthoáng cho pheùp baûoñaûm tính oånñònh vaø
beàn vöõng.
nKhuyeát:
nCaàn moâ hình toaùnñeåthieát keáboäñieàu khieån.
nCaàn hieåu bieát saâu veàkyõ thuaätñieàu khieån.
nThöôøng khoâng hieäu quaûkhiñieàu khieån heäphi tuyeán.
nKhoâng söûduïng kinh nghieäm cuûa con ngöôøi.
4
“Thoâng minh”laøgì?
nThoâng minh laøkhaûnaêng thu thaäp vaøsöû
duïng tri thöùc.
nCoùnhieàu caápñoäthoâng minh vaønhieàu loaïi
thoâng minh.
nKhaùi nieäm“Thoâng minh”chæmang tính
töôngñoái. (Moät heäthoáng ngöôøi naøy cho laø
thoâng minh, ngöôøi khaùc coùtheåcho laø
khoâng thoâng minh…)

5
So saùnh
ÑK thoâng minh-ÑK thoâng thöôøng
nVeàmaët toaùn hoïc,ñieàu khieån thoâng minh khoâng
chaët cheõ baèngñieàu khieån thoâng thöôøng.Ñaây laø
lónh vöïc töôngñoái môùi, chöañöôïc nghieân cöùu
heát.
nVeànguyeân taéc, khi thieát keácaùc boäñieàu khieån
thoâng minh, takhoâng caàn moâ hình toaùn hoïc cuûa
ñoái töôïng ®ñaây laøöuñieåm cuûañieàu khieån
thoâng minh, vìnhieàu tröôøng hôïp khoâng deã (hoaëc
khoâng theå) xaùcñònh moâ hình toaùn cuûañoái töôïng.
6
Phaàn 1:ÑIEÀU KHIEÅN MÔØ
n1965: Lofti A. Zadehñöa ra khaùi nieäm veàlyùthuyeát taäp
môø(fuzzy set).
n1972: Terano vaøAsai laäp cô sôûnghieân cöùu heäthoáng môø
ôûNhaät.
n1974: Mamdani nghieân cöùuñieàu khieån môøcho loøhôi.
n1980: haõng Smidth nghieân cöùuñieàu khieån môøcho loøxi-
maêng.
n1983: haõng Fuji Electric nghieân cöùuöùng duïngñieàu khieån
môøcho nhaømaùy xöûlyùnöôùc.
n1984: Hieäp hoäi Heäthoáng Môøquoác teáIFSAñöôïc thaønh
laäp.
n1989: phoøng thínghieäm quoác teánghieân cöùuöùng duïng kyõ
thuaät môøñaàu tieânñöôïc thaønh laäp.
Lòch söûphaùt trieån
7
Taäp hôïp kinhñieån
Caùch bieåu dieãn taäp hôïp:
nBieåu dieãn baèng caùch lieät keâ phaàn töû:
VD:A = {1, 2, 3, 5, 7, 11}
®Baát tieän khi taäp hôïp coùnhieàu (voâ soá) phaàn töû.
nBieåu dieãn thoâng qua tính chaát phaàn töû:
VD:A = {x |x laøsoánguyeân toá}
B = {x |x laøsoáthöïc vaøx < 4}
8
Cho Xlaøtaäp hôïp caùcñoái töôïng coùcuøng tính
chaát (taäp cô sôû). Alaøtaäp con cuûa X. Phaàn töû
x baát kyøthuoäc X. AÙnh xaï
c
A:X®{0, 1} xa
{0, 1} xaùùc
c
ñ
ñònh bô
ònh bôûûi:
i:
ñöôïc goïi laø haømñaëc tröng (haøm chæthò) cuûa
A.
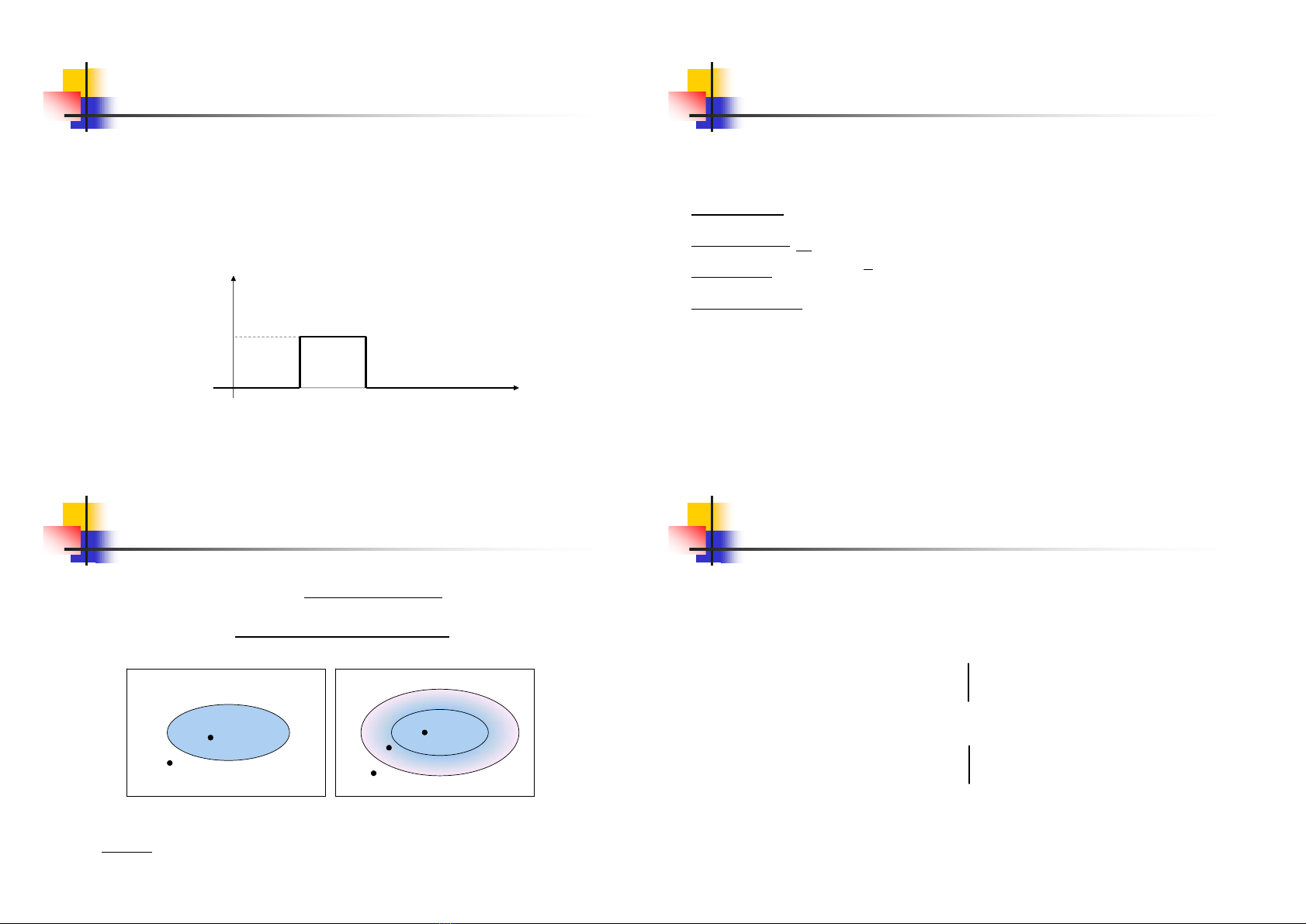
Heäquaû:
c
X(x) = 1 vôùi moïi xÎX
Haømñaëc tröng
î
í
ì
Ï
Î
=)(0
)(1
)( Ax
Ax
x
A
c
9
VD: Cho A= {xÎR
R|2 < x < 4}, thì:
c
A(1,5) = 0
c
A(3) = 1
c
A(2) = 0
c
A(4) = 0
Haømñaëc tröng
24
1
c
A
x
10
Cho 2 taäp hôïp A,Bñònh nghóa treân taäp cô sôû X. Ta coù
caùc tính chaát sau:
Pheùp hôïp:AÈBÞ
c
A
AÈB(x) = max{
c
A(x),
c
B(x)}
Pheùp giao:AÇBÞ
c
AÇB(x) = min{
c
A(x),
c
B(x)}
Pheùp buø:
Chöùa trong:AÍBÞ
c
A(x)£
c
B(x)
Kieåm chöùng caùc keát quaûtreân baèng caùc víduïcuïtheå.
VD:A = {xÎR
R|2 < x < 4}, B ={xÎR
R|1 < x < 5}
Haømñaëc tröng
)(1)( xxA A
A
cc
-=Þ
11
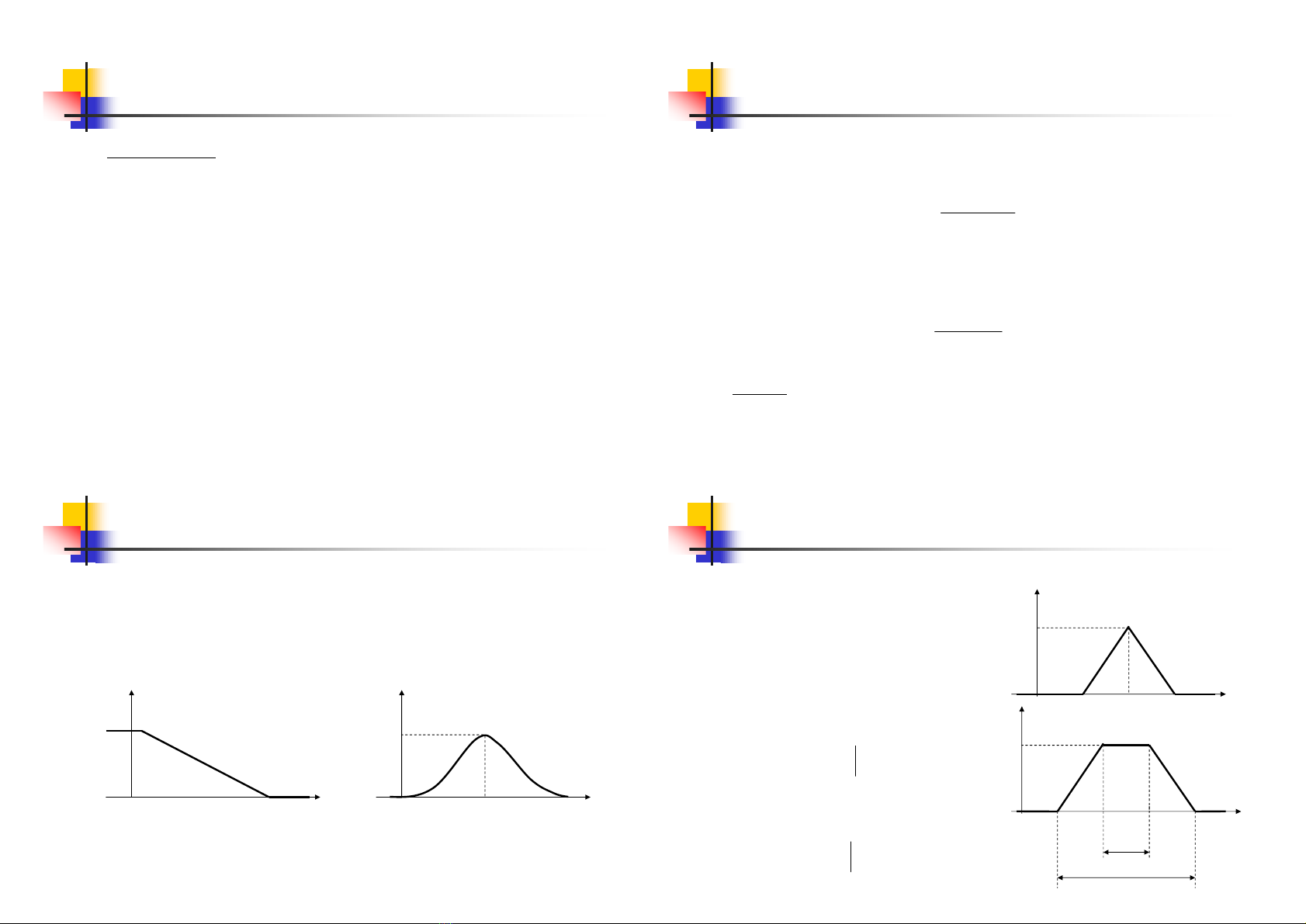
nTaäp kinhñieån coùbieân roõ raøng (hình a).
nTaäp môøcoùbieân khoâng roõ raøng (hình b).
Taäp môø(Fuzzy set)
x1
x2
X X
x1
x2
x3
A
A
~
(a)(b)
Ghi chuù: Ta duøng chöõ caùi coùdaáu ngaõ treânñeåñaët teân cho taäp môø.
12
VD: Xeùt nhöõng taäpñöôïc moâ taû“môø”sauñaây:
-Taäp goàm nhöõng soáthöïc nhoûhôn nhieàu so
vôùi 6.
Taäp môø(Fuzzy set)
}6{
~
<<Î= xRxB
B
~
-Taäp goàm nhöõng soáthöïc gaàn baèng 3.
C
~
}3{
~
»Î= xRxC
Vaäy: x= 3,5 coùthuoäc taäp hay khoâng?
x= 2,5 coùthuoäc taäp hay khoâng?
B
~
C
~
13
nÑònh nghóa:Taäp môø xaùcñònh treân taäp cô sôû Xlaø
moät taäp hôïp maømoãi phaàn töûcuûa noùlaømoät caëp giaù
trò , trongñoù xÎXvaølaøaùnh xaï:
nAÙnh xaïñöôïc goïi laø haøm lieân thuoäc
(membership function) cuûa taäp môø.
nHaøm lieân thuoäc cho bieátñoäphuïthuoäc cuûa caùc phaàn
töûvaøo taäp môø(phaàn töûthuoäc taäp môøbao nhieân phaàn
traêm).
Taäp môø(Fuzzy set)
[
]
1,0:
~®X
A
m
A
~
))(,( ~xx A
m
)(
~x
A
m
)(
~x
A
m
A
~
14
nTaäp môø ñònh nghóa treân taäp cô sôû Xrôøi raïc höõu
haïnñöôïc kyùhieäu nhösau:
nTaäp môø ñònh nghóa treân taäp cô sôû Xlieân tuïc voâ
haïnñöôïc kyùhieäu nhösau:
Ghi chuù: Daáu gaïch ngang khoâng phaûi laødaáu chia maøchælaødaáu phaân
caùch; daáu åvaø òkhoâng phaûi laøtoång hay tích phaân maøchælaøkyùhieäu coùyù
nghóa“goàm caùc phaàn töû”.
Kíhieäu taäp môø
A
~
þ
ý
ü
î
í
ì
=å
ii
i
A
x
x
A)(
~~
m
A
~
þ
ý
ü
î
í
ì
=òx
x
AA)(
~~
m
15
Haøm lieân thuoäc coùtheåcoùdaïng trôn (hình a),
hay daïng tuyeán tính töøngñoaïn (hình b).
Haøm lieân thuoäc
6x
1
B
~
)(
~x
B
m
(a) 3x
1C
~
)(
~x
C
m
(b)
16
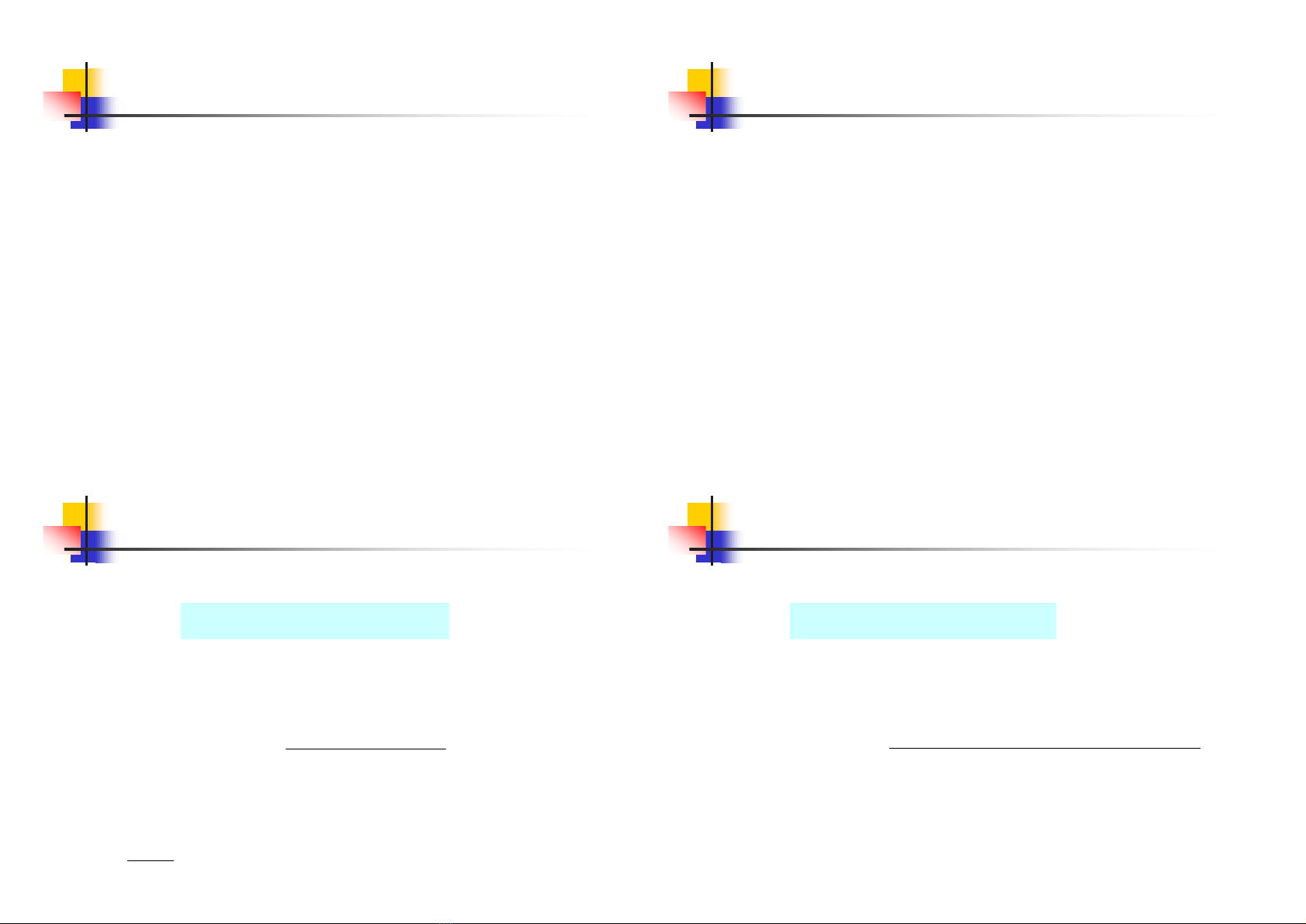
nTam giaùc, hình thang.
Ñoäcao:
Mieàn tin caäy:
Mieàn xaùcñònh:
Caùc daïng haøm lieân thuoäc
80x
1
)(~x
A
m
4060
x
1
)(
~x
A
m
20406080
Mieàn xaùcñònh
Mieàn tin caäy
)(sup)
~
(~xAhgt A
Xx
m
Î
=
{
}
1)(
~=Î= xXxT A
m
{
}
0)(~>Î= xXxS A
m
17
nCaùc haøm lieân thuoäc coùdaïng trôn nhö: daïng
gauss, daïng chuoâng daïng sigmoid,…ít
ñöôïc söûduïng hôn do tính toaùn phöùc taïp.
nThöôøng duøng haøm lieân thuoäc daïng hình
thang, vaøhình tam giaùc.
Caùc daïng haøm lieân thuoäc
18
nTaäp môøcoùñoäcao = 1 goïi laø taäp môøchính
taéc.
Taäp môøchính taéc
19
PHEÙP HÔÏP 2 TAÄP MÔØ
Caùc coâng thöùc laáy hôïp 2 taäp môø:
nCoâng thöùc Zadeh (thöôøng duøng trongñkhieån môø):
nCoâng thöùc Lukasiewicz (bounded sum):
nCoâng thöùc Einstein:
nCoâng thöùc xaùc suaát:
{
}
()max(),()
ABAB
xxx
mmm
È
=
{
}
()min1,()()
ABAB
xxx
mmm
È
=+
()()
()
1()()
AB
AB
AB
xx
x
xx
mm
mmm
È
+
=++
()()()()()
ABABAB
xxxxx
mmmmm
È
=+-
Ghi chuù: Töøñaây veàsau, ta seõ chænoùi veàtaäp môø, neân nhöõng daáu ngaõ bieåu thò taäp
môøtreân caùc chöõ caùi seõñöôïc boûñiñeåñôn giaûn trong caùch vieát. 20
PHEÙP GIAO 2 TAÄP MÔØ
Caùc coâng thöùc laáy giao 2 taäp môø:
nCoâng thöùc Zadeh (thöôøng duøng trongñkhieån môø):
nCoâng thöùc Lukasiewicz:
nCoâng thöùc Einstein:
nCoâng thöùc xaùc suaát:
{
}
()min(),()
ABAB
xxx
mmm
Ç
=
{
}
()max0,()()1
ABAB
xxx
mmm
Ç
=+-
()
()()
()
2()()()()
AB
AB
ABAB
xx
x
xxxx
mm
mmmmm
Ç=
-+-
()()()
ABAB
xxx
mmm
Ç
=












![Đề thi cuối học kì 1 môn Máy và hệ thống điều khiển số năm 2025-2026 [Kèm đáp án chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251117/dangnhuy09/135x160/4401768640586.jpg)




![Tự Động Hóa Thủy Khí: Nguyên Lý và Ứng Dụng [Chi Tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250702/kexauxi10/135x160/27411767988161.jpg)








