30 BÀI TOÁN BĐT - Cực Trị
trong các Đề thi OLYMPIC Toán Học 10
Bài Toán 1. (THPT Quốc Học Huế)
Cho các số thực a,b,x,ythỏa mãn điều kiện ax −by =p3. Tìm giá trị nhỏ nhất của biểu
thức:
F=a2+b2+x2+y2+bx +ay.
Lời giải.
Ta có:F=µx+b
22
+³y+a
2´2
+3
4(a2+b2). Đặt:M=(x;y), A=µ−b
2;−a
2,(∆) : ax −by =p3.
Ta có: M A2=µx+b
22
+³y+a
2´2
.Mà M∈(∆)nên M A2≥[d(A;∆)]2=3
a2+b2
Dấu ‘=’ xảy ra khi M là hình chiếu của A trên (∆).
Suy ra F≥3
a2+b2+3
4(a2+b2)≥2r3
a2+b2.3
4(a2+b2)=3
Vây MinF=3đạt được chẳng hạn khi (a;b;x;y)=Ãp2; 0; p6
2;p2
2!.
Bài Toán 2. (THPT Chu Văn An - Ninh Thuận)
Cho x,y,zdương. Chứng minh rằng:
x
y+z+25y
z+x+4z
x+y>2.
Lời giải.
Đặt:
a=y+z
b=z+x
c=x+y=⇒
x=b+c−a
2
y=a+c−b
2
z=a+b−c
2
. Do x,y,zdương =⇒
a,b,c>0
b+c>a
a+c>b
a+b>c
(1)
Khi đó ta có:
x
y+z+25y
z+x+4z
x+y=b+c−a
2a+25(a+c−b)
2b+4(a+b−c)
2c
=µb
2a+25a
2b+µc
2a+2a
c+µ25c
2b+2b
c−15 ≥2. 5
2+2.1 +2.5 −15 (AM −GM)
Đẳng thức xảy ra khi
b
2a=25a
2b
c
2a=2a
c
25c
b=2b
c
⇐⇒
b=5a
c=2a
5c=2b⇐⇒ a
1=b
5=c
2=a+2c
5
1
=⇒ b=a+2c>a+cmâu thuẫn với (1). =⇒ Dấu ‘=’ không xảy ra.
Vậy x
y+z+25y
z+x+4z
x+y>2. (Dpcm)
Bài Toán 3. (THPT Chuyên Huỳnh Mẫn Đạt-Kiên Giang)
Cho các số thực dương a,b,cthỏa mãn :
4≥a≥b≥c>0; 3abc ≤min{6a+8b+12c; 72}; 2ab ≤mi n{3a+4b;24}.
Tìm giá trị lớn nhất của biểu thức:
P=a2+b2+c2+a+b+c.
Lời giải.
4+3+2=cµ4
a+3
b+2
c+(b−c)µ4
a+3
b+(a−b)4
a
≥c.3 3
r24
abc +(b−c).2r12
ab +(a−b)
≥3c+2(b−c)+(a−b)=a+b+c
⇒a+b+c≤9 (1). Dấu ‘=’ xảy ra khi a=4; b=3; c=2.
Ta lại có:
42+32+22=c2µ42
a2+32
b2+22
c2+(b2−c2)µ42
a2+32
b2+(a2−b2)42
a2
42
a2+32
b2+22
c2≥4
a.3
b+3
b.2
c+4
a.2
c=12c+6a+8b
abc ≥3
42
a2+32
b2≥1
2µ4
a+3
b2
=1
2µ4b+3a
ab 2
≥2
Suy ra: 42+32+22≥3c2+2(b2−c2)+(a2−b2)=a2+b2+c2(2)
Từ (1) và (2) ta suy ra:P≤38.Dấu ‘=’ xảy ra ⇐⇒ a=4,b=3, c=2
Vậy M axP=38. Đạt khi a=4, b=3, c=2.
Bài Toán 4. (THPT Chuyên Lê Quý Đôn - Khánh Hòa)
Cho x>1; y>2; z>3; 1
x+2
y+3
z=2. Chứng minh rằng:
px+y+z≥px−1+py−2+pz−3.
Lời giải.
Ta có: px−1+py−2+pz−3=px.rx−1
x+py.sy−2
y+pz.rz−3
z
Theo BĐT BCS suy ra:
px−1+py−2+pz−3≤px+y+z.sx−1
x+y−2
y+z−3
z
⇐⇒ px−1+py−2+pz−3≤px+y+z.s3−µ1
x+2
y+3
z
⇐⇒ px−1+py−2+pz−3≤px+y+z(Dpcm)
2
Bài Toán 5. (THPT Chuyên Tiền Giang-Tiền Giang)
Cho các số thực a,b,c,dthỏa: a2+b2=1; c+d=3. Chứng minh rằng:
ac +bd +cd ≤9+6p2
4.
Lời giải.
Goi M(a;b), N(c,d). Vì a2+b2=1nên điểm Mnằm trên đường tròn (C) : x2+y2=1.
Vì c+d=3nên Nnằm trên đường thẳng ∆:x+y−3=0
Ta có:M N 2=(c−a)2+(d−b)2=a2+b2+c2+d2−2ac −2bd
=a2+b2+(c+d)2−2cd −2ac −2bd =10 −2(ac +bd +cd )
Suy ra: ac +bd +cd =5−M N 2
2. Kẻ OH⊥∆,OH ∩(C)=K.
Ta thấy M N ≥HK ⇒ac +bd +cd ≤5−HK 2
2
Do KÃp2
2;p2
2!,Hµ3
2;3
2nên HK 2=11 −6p2
2
Suy ra ac +bd +cd ≤5−11 −6p2
4=9+6p2
4.(Dpcm)
Bài Toán 6. (THPT Chuyên Lê Hồng Phong - TP.HCM)
Cho a,b,clà dộ dài 3 cạnh của một tam giác thỏa mãn: a2+b2+c2+1=2(ab +bc +ca). Tìm
giá trị nhỏ nhất của biểu thức:
P=9(a2+b2+c2)−2ab −2bc −14ca.
Lời giải.
Đặt:
x=b+c−a
y=c+a−b
z=a+b−c=⇒ x,y,z>0; a=y+z
2;b=z+x
2;c=x+y
2.
Ta có:
a2+b2+c2+1=2(ab +bc +ca)
⇐⇒³y+z
2´2
+³z+x
2´2
+³x+y
2´2
+1=2³y+z
2
z+x
2+z+x
2
x+y
2+x+y
2
y+z
2´
⇐⇒x y +yz +zx =1.
P=9·³y+z
2´2
+³z+x
2´2
+³x+y
2´2¸−2y+z
2
z+x
2−2z+x
2
y+z
2−14 x+y
2
y+z
2=4(x2+z2)+y2
Với mọi α>0ta có:
αx2+y2
2≥2rα
2x y;αz2+y2
22rα
2z y và rα
2(x2+z2)≥2rα
2xz
=⇒ µα+rα
2(x2+z2)+y2≥2rα
2¡x y +y z +zx¢=2rα
2(1)
Ta đi tìm αthỏa mãn:
α>0
α+rα
2=4⇐⇒
α>0
2µrα
22
+rα
2−4=0⇐⇒ rα
2=p33 −1
4⇐⇒ α=17 −p33
4
3
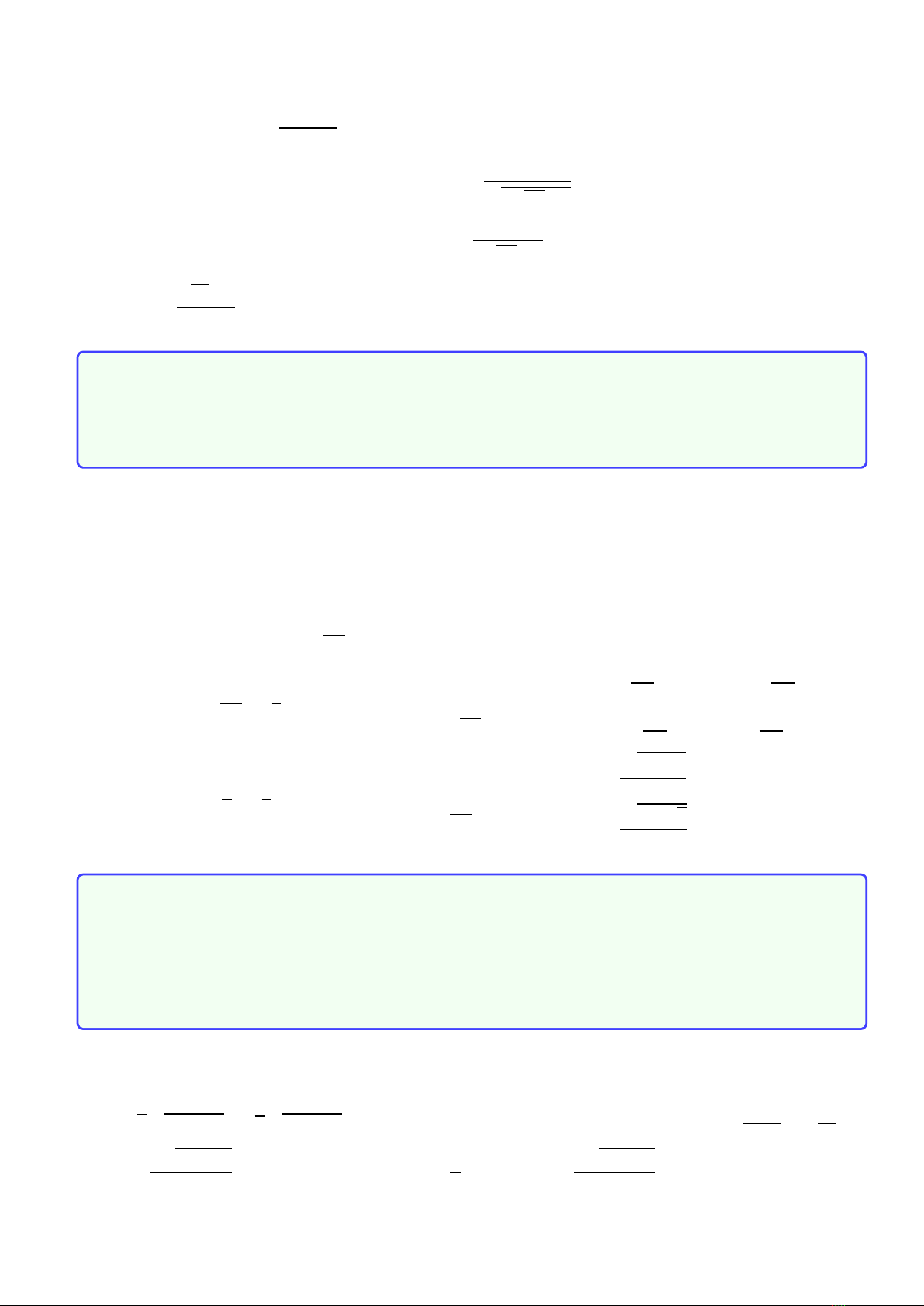
Suy ra (1) trở thành: P≥p33 −1
2.
Dấu ‘=’ xảy ra khi
x,y,z>0
x y +y z +zx =1
2αx2=y2
2αz2=y2
x=z
⇐⇒
x=z=1
p2p2α+1
y=s2α
2p2α+1
Vậy MinP=p33 −1
2.
Bài Toán 7. (THPT Chuyên Bến Tre - Bến Tre)
Cho x2+y2−x y =1. Tìm Min và Max của biểu thức:
M=x4+y4−x2y2.
Lời giải.
Ta có: x2+y2−x y =1=⇒ (1=x2+y2−x y ≥2x y −x y =x y
1=(x+y)2−3x y ≥−3x y =⇒ −1
3≤x y ≤1
Mặt khác x2+y2−x y =1⇐⇒ x2+y2=1+x y nên: M=(x2+y2)−3x2y2=−2x2y2+2x y +1
Đặt t=x y =⇒ M=−2t2+2t+1. Vậy cần tìm Min và Max của tam thức bậc hai:
f(t)=−2t2+2t+1trên đoạn ·−1
3;1¸.
Ta có: Mi nM=fµ−1
3=1
9.Đạt được khi
x2+y2−x y =1
x y =−1
3⇐⇒
x=p3
3
y=−p3
3
hay
x=−p3
3
y=p3
3
.
Ta có: MaxM=fµ1
2=3
2. Đạt được khi
x2+y2−x y =1
x y =−1
3⇐⇒
x=p3+p5
2
y=p3−p5
2
Bài Toán 8. (THPT Lê Quý Đôn - Quảng Trị)
Cho hai số dương avà b.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
A=xpa+y+ypa+x.
Với x,ylà các số thực không âm và x+y=b.
Lời giải.
Áp dụng BĐT BCS ta có:
A2=(pxpax +x y +pypa y +x y )2≤(x+y)(ax +ay +2x y)=b(ab +2x y)≤ab2+2b³x+y
2´2
=b2
2(2a+b)
=⇒ A≤bp4a+2b
2.Dấu ‘=’ xảy ra khi x=y=b
2.Vậy M axA=bp4a+2b
2.
4
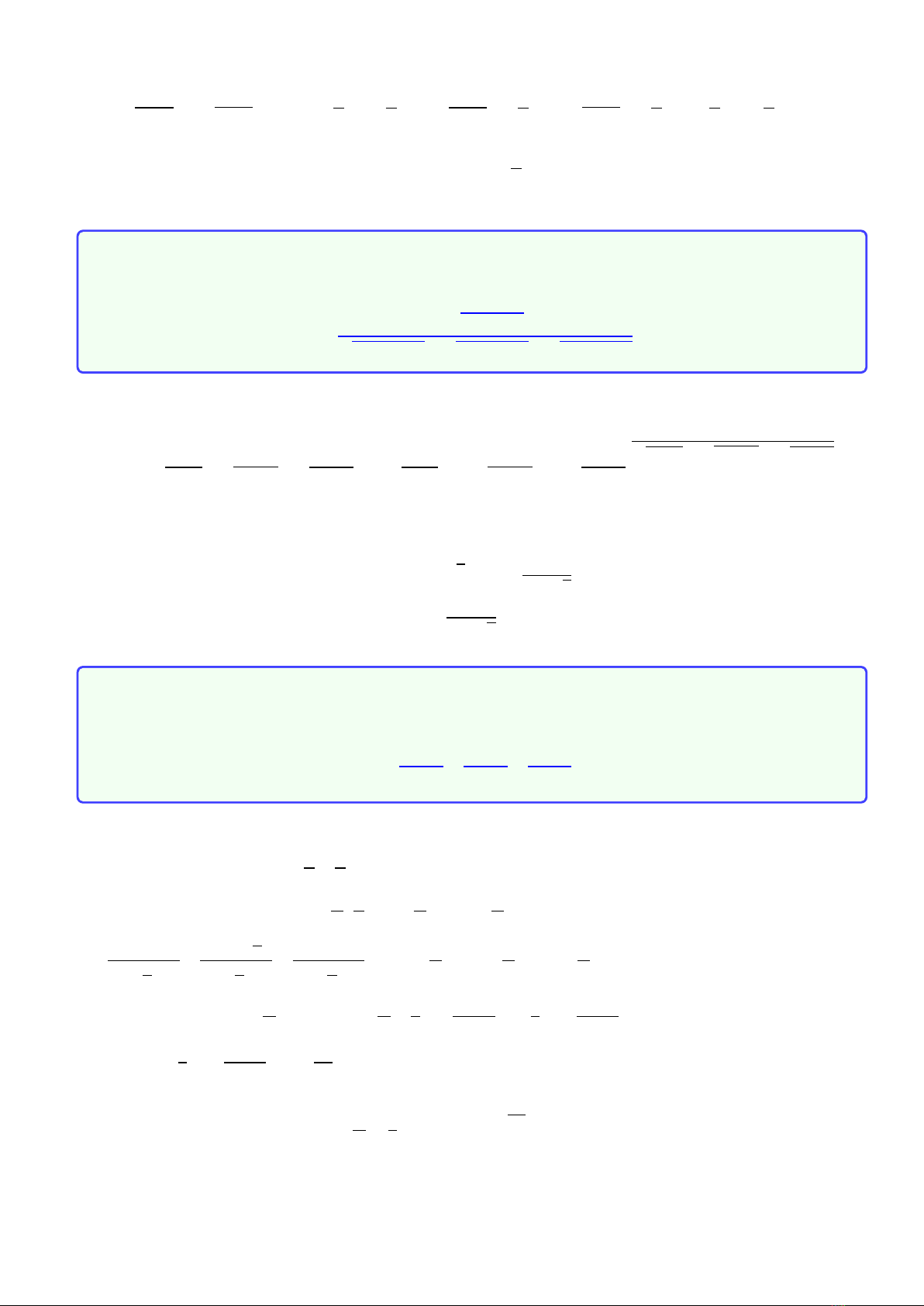
A=xpa+y+ypa+x−(x+y)pa+bpa=x(pa+y−pa)+y(pa+x−pa)+bpa≥bpa
(Do x,ylà các số thực không âm).
Dấu ‘=’ xảy ra khi (x=0
y=bhay (x=b
y=0. Vậy Mi nA=bpa.
Bài Toán 9. (THPT Chuyên Lý Tự Trọng - Cần Thơ)
Cho 3 số thực dương a,b,cthỏa mãn : a2+b2+c26=0. Tìm Max của biểu thức:
P=pa+b+c
p2a+b+c+pa+3b+c+pa+b+4c
.
Lời giải.
Không mất tính tổng quát,chuẩn hóa a+b+c=1. Khi đó ta có: P=1
pa+1+p2b+1+p3c+1
.
Đặt: m=pa+1+p2b+1+p3c+1,c=pa+1, y=p2b+1, z=p3c+1.
Suy ra:m2=4+2(x y +yz +zx)+b+2c≥4+2(x y +y z +zx)=>2(x y +yz +zx)≤m2−4 (1)
Ta có: 2£(x−1)(y−1) +(y−1)(z−1) +(z−1)(x−1)¤≥0
⇐⇒ 2(x y +yz +zx)−4m+6≥0⇐⇒ 2(x y +yz +zx)≥4m−6 (2)
Từ (1) và (2) suy ra: m2−4m+2≥0⇒m≥2+p2⇒P≤1
2+p2.
Dấu ‘=’ xảy ra khi a=1; b=c=0. Vậy M axP=1
2+p2
.
Bài Toán 10. (THPT Chuyên Thăng Long - Đà Lạt Lâm Đồng)
Xét các số thực dương x,y,zthỏa mãn điều kiện x y z +x+z=y.Tìm giá trị lớn nhất của biểu
thức:
P=2
x2+1−2
y2+1+3
z2+1.
Lời giải.
Ta có: x y z +x+z=y⇔xz +x
y+z
y=1. Vì x,y,z>0nên tồn tại các góc A,B,C∈(0;π)
sao cho A+B+C=πvà x=tan A
2,1
y=tan B
2,z=tan C
2.Từ đó ta có:
P=2
tan2A
2+1−
2tan2B
2
tan2B
2+1+3
tan2C
2+1=2cos2A
2−2sin2B
2+3cos2C
2
=cos A+cosB−3sin2C
2+3=−3µsin C
2−1
3cos A−B
22
+1
3cos2A−B
2+3
=⇒ P≤1
3cos2A−B
2+3≤10
3.
Dấu ‘=’ xảy ra khi và chỉ khi
b
A=b
B
sin C
2=1
3
Vậy M axP=10
3.
5