Ketnooi.com diễn đàn chia sẻ kiến thức, công nghệ
Cơ Học Lưu Chất
Page 1 of 27
BÀI TẬP CHƯƠNG I
MỞ ĐẦU
Bài 1.1
Để làm thí nghiệm thủy lực, người ta đổ đầy nước vào một đường ống có đường kính d =
300mm, chiều dài L = 50m ở áp suất khí quyển. Hỏi lượng nước cần thiết phải đổ vào ống là bao
nhiêu để áp suất đạt tới 51at ? Biết hệ số nén ép
1
20000
1
at
p
Giải
Lượng nước cần thiết phải đổ vào ống để áp suất tăng lên 51at là :
Ta có hệ số giãn nở do áp lực :
dpVdV
dp
dV
Vpp ..
1
Do
dpdV,
đồng biến nên :
dpVdV
dp
dV
Vpp ..
1
Mà thể tích
3
22
5325,350.
4
)3.0.(14,3
.
4
.
.mL
d
LSV
)(84,8)(10.84,8)151.(5325,3.
20000
133 litermdV
Vậy cần phải thêm vào ống 8.84 lít nước nữa để áp suất tăng từ 1at lên 51at.
Bài 1.2
Trong một bể chứa hình trụ thẳng đứng có đường kính d = 4m, đựng 100 tấn dầu hỏa có khối
lượng riêng
3
/850 mkg
ở 100C. Xác định khoảng cách dâng lên của dầu trong bể chứa khi
nhiệt độ tăng lên đến 400C. Bỏ qua giãn nở của bể chứa. Hệ số giãn nở vì nhiệt
10
00072,0
C
t
.
Giải
Khối lượng riêng của dầu hỏa là :
Hệ số giãn nở do nhiệt độ :
)(542,2
85
216
)3040.(
17
2000
.00072,0..
13
mdtVdV
dt
dV
Vtt
Mà :
)(202,0
4.14,3
542,2.4
.
4
.
4
.
22
2
m
d
dV
hh
d
dV
Vậy khoảng cách dầu dâng lên so với ban đầu là 0.202(m)
Bài 1.3
Khi làm thí nghiệm thủy lực, dùng một đường ống có đường kính d = 400mm, dài L = 200m,
đựng đầy nước ở áp suất 55 at. Sau một giờ áp suất giảm xuống còn 50 at. Xác định lượng nước
chảy qua các kẽ hở của đường ống. Hệ số nén ép
1
20000
1
at
p
.
Giải
Hệ số giãn nở do áp lực :
dpL
d
dpVdV
dp
dV
Vppp ..
4
.
..
12
Ketnooi.com diễn đàn chia sẻ kiến thức, công nghệ
Cơ Học Lưu Chất
Page 2 of 27
)(28,6)(10.28,6)5550(.200.
4
4,0.14,3
20000
133
2
litermdV
Vậy lựơng nước chảy qua khe hở đường ống là 6.28 (liter)
Bài 1.4
Một bể hình trụ đựng đầy dầu hỏa ở nhiệt độ 50C, mực dầu cao 4m. Xác định mực dầu tăng lên,
khi nhiệt độ tăng lên 250C. Bỏ qua biến dạng của bể chứa. Hệ số giãn nở vì nhiệt
10
00072.0
C
t
.
Giải
Hệ số giãn nở do nhiệt độ :
dtVdV
dt
dV
Vtt ..
1
Mà thể tích ban đầu là :
h
d
V.
4
.2
Thể tích dầu tăng lên :
h
d
dV 4
.2
)(58)(058,0)525.(4.00072,0..
.
1
mmmdthh
dth
h
dt
dV
V
t
t
Ketnooi.com diễn đàn chia sẻ kiến thức, công nghệ
Cơ Học Lưu Chất
Page 3 of 27
BÀI TẬP CHƯƠNG II
THỦY TĨNH HỌC
Bài 2.1
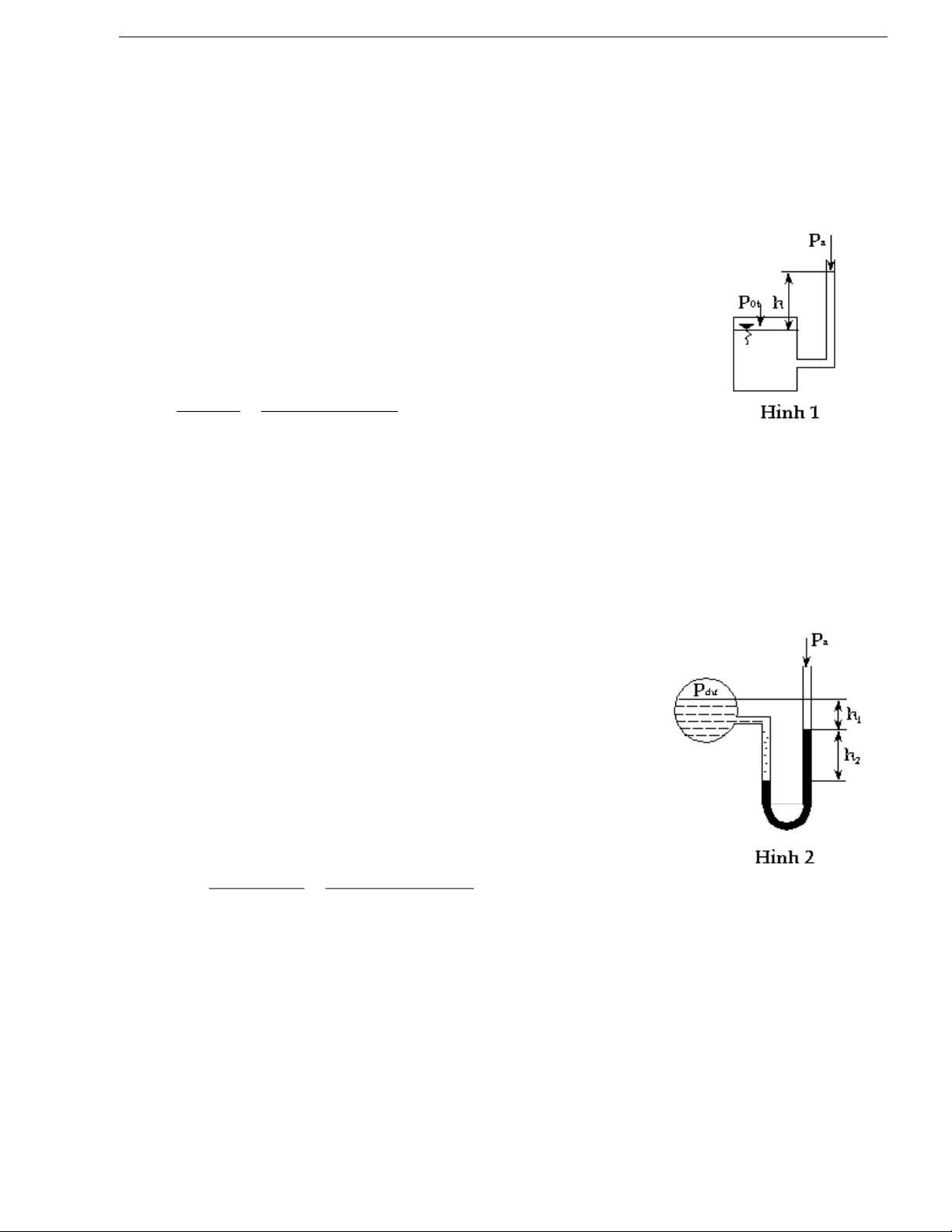
Xác định độ cao của cột nước dâng lên trong ống đo áp (h). Nước trong bình kín chịu áp suất tại
mặt tự do là
atpt06.1
0
. Xác định áp suất
t
p0
nếu h = 0.8m.
Giải
Chọn mặt đẳng áp tại mặt thoáng của chất lỏng.
Ta có :
BA pp
Mà
hpp
hpp
pp
a
B
A.
,0
0
0
)(6,0
9810
10.81,9).106,1( 4
0m
pp
ha
Nếu h=0,8m thì
)(08,1/105948981008,0.9810. 2
0atmNphp a
Bài 2.2
Một áp kế đo chênh thủy ngân, nối với một bình đựng nước.
a) Xác định độ chênh mực nước thủy ngân, nếu h1 = 130mm và áp suất dư trên mặt nước
trong bình 40000 N/m2.
b) Áp suất trong bình sẽ thay đổi như thế nào nếu mực thủy ngân trong hai nhánh bằng nhau.
Giải
a) Xác định độ chênh mực thủy ngân (tìm h2) :
Chọn mặt đẳng áp như hình vẽ :
Ta có :
BA pp
).( 21
2
0hhpp OHA
2
.hpp HgaB
221
2
0.).( hphhp HgaOH
1
2
0
2
2.)()( hpph OHaOHHg
Mà
da ppp
0
Vậy :
)(334,0
98100132890
013,0.981040000
)(
.
2
1
2
2m
hp
h
HgOH
OHd
b) Áp suất trong bình khi mực thủy ngân trong hai nhánh bằng nhau :
Ta có :
DC pp
hpp OHC .
2
0
aD pp
aOH php .
2
0
ckaOH ppph 0
2.
Ketnooi.com diễn đàn chia sẻ kiến thức, công nghệ
Cơ Học Lưu Chất
Page 4 of 27
)(0297,057,2913)334,0.
2
1
13,0.(9810
).(.2
2
1
1
22
at
hhhp OHOHck
Bài 2.3
Một áp kế vi sai gồm một ống chữ U đường kính d = 5mm nối hai bình có đường kính D = 50mm
với nhau. Máy đựng đầy hai chất lỏng không trộn lẫn với nhau, có trọng lượng riêng gần bằng
nhau : dung dịch rượu êtylic trong nước (
3
1/8535 mN
) và dầu hỏa (
3
2/8142 mN
). Lập
quan hệ giữa độ chênh lệch áp suất
21 ppp
của khí áp kế phải đo với độ dịch chuyển của
mặt phân cách các chất lỏng (h) tính từ vị trí ban đầu của nó (khi
0p
). Xác định
p
khi h =
250mm.
Giải
a) Lập mối quan hệ giữa độ chênh lệch áp suất
21 ppp
:
Chọn mặt đẳng áp như hình vẽ :
Khi
)(0 21 ppp
: thì mặt phân cách giữa hai lớp chất lỏng khác nhau ở vị trí cân bằng
O :
o
BA pp
o
111 .hppA
o
222 .hppB
Theo điều kiện bình thông nhau :
1
22
12211.
h
hhh
Khi
)(0 21 ppp
: thì mực nước trong bình 1 hạ xuống 1 đoạn
h
và đồng thời mực
nước bình 2 tăng lên 1 đoạn
h
. Khi đó mặt phân cách di chuyển lên trên 1 đoạn h so với
vị trí O.
).( 111 hhppA
hhhhppB.).( 1222
Theo tính chất mặt đẳng áp ta có :
(*)].[).().(
.).().(
.).().(
2211212121
1112221
1222111
hhhhpp
hhhhhhpp
hhhhphhp
Ta thấy thể tích bình 1 giảm một lượng :
h
d
V 4
.2
Thể tích trong ống dâng lên một lượng :
h
d
V4
.2
'
Ta có
h
D
d
hVV 2
2
'
và
2211.hh
thay vào (*)
Ketnooi.com diễn đàn chia sẻ kiến thức, công nghệ
Cơ Học Lưu Chất
Page 5 of 27
Ta được :
).()(
).().(
21
2
2
21
21
2
2
2121
D
d
h
h
D
d
hppp
Tính
p
khi h = 250mm
Ta có :
2
2
2
/14081428535
05,0
005,0
8142853525,0 mNp
ĐS : a/
).()( 21
2
2
21
D
d
hp
b/
2
/140 mNp
Bài 2.4
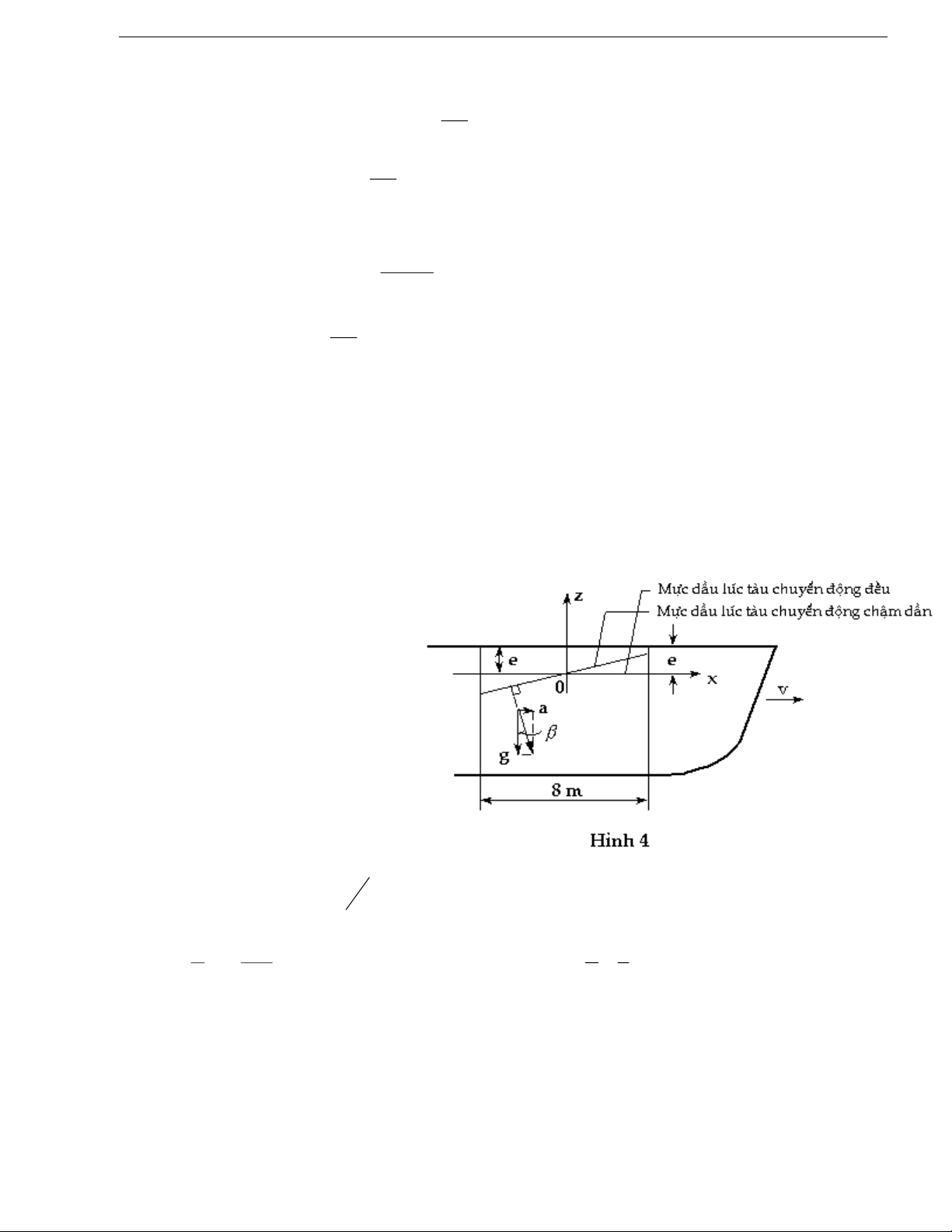
Xác định vị trí của mặt dầu trong một khoang dầu hở của tàu thủy khi nó chuyển động chậm dần
đều trước lúc dừng hẳn với gia tốc a = 0.3 m/s2. Kiểm tra xem dầu có bị tràn ra khỏi thành
không, nếu khi tàu chuyển động đều, dầu ở cách mép thành một khoảng e = 16cm. Khoảng
cách tàu dài L = 8m.
Giải
Chọn hệ trục tọa độ như hình vẽ, ta
biết mặt tự do của dầu là mặt đẳng
áp.
Phương trình vi phân mặt đẳng áp :
(*)0 ZdzYdyXdx
Có :
gZYaX ;0;
thay vào (*)
(*)
0 gdzadx
Tích phân ta được :
Czgxa ..
Vì mặt tự do của dầu đi qua gốc tọa
độ O (x=0, z=0)
0C
.
Nên phương trình mặt tự do sẽ là :
0.. zgxa
Có
tgxz .
trong đó
g
a
tg
Như vậy mặt dầu trong khoang là mặt phẳng nghiêng về phía trước :
)(24,12)(1224,0
81,9
3,0
.4. cmm
g
a
xz
với
)(4
2
8
2m
L
x
Ta thấy z = 12,24 (cm) < e = 16 (cm) nên dầu không tràn ra ngoài.
Bài 2.5
Một toa tàu đi từ ga tăng dần tốc độ trong 10 giây từ 40 km/h đến 50 km/h. Xác định áp suất
tác dụng lên điểm A và B. Toa tàu hình trụ ngang có đường kính d = 2,5m, chiều dài L = 6m.
Dầu đựng đầy một nửa toa tàu và khối lượng riêng của dầu là 850 kg/m3. Viết phương trình mặt
đẳng áp và mặt tự do của dầu.