Bài t p ch ng 1 ậ ươ
1. Đ i các s nh phân sau sang s th p phân: ổ ố ị ố ậ
a. 10110 d. 1111010111
b. 10001101 e. 10111111
c. 100100001001
2. Đ i các giá tr th p phân sau sang nh phân:ổ ị ậ ị
a. 37
b. 14
c. 189
d. 205
e. 2313
f. 511
3. Giá tr th p phân l n nh t c a s nh phân 8 bit là bao nhiêu,16 bit là bao nhiêu?ị ậ ớ ấ ủ ố ị
4. Đ i các s bát phân sang s th p phân t ng ng: ổ ố ố ậ ươ ứ
a. 743
b. 36
c. 3777
d. 257
e. 1204
5. Đ i các s th p phân sau sang s bát phân:ổ ố ậ ố
a. 59
b. 372
c. 919
d. 65,535
e. 255
6. Đ i các s bát phân bài 4 thành s nh phân. ổ ố ở ố ị
7. Đ i các s nh phân bài 1 thành s bát phân. ổ ố ị ở ố
8. Đ i các giá tr hex sau thành s th p phân: ổ ị ố ậ
a. 92
b. 1A6
c. 37FD
e. 2C0
f. 7FF
9. Đ i các giá tr th p phân sau sang Hex: ổ ị ậ
a. 75
b. 314
c. 2048
d. 25,619
e. 4095
10. Hãy mã hóa các s th p phân sau thành s BCD, sau đó đ i sang s BCD âm: ố ậ ố ổ ố
a. 47
b. 962
c. 187
d. 42,689.627
e. 1204
11. Đ i nh ng s BCD sau thành s th p phân: ổ ữ ố ố ậ
a. 10010110101010010
b. 000110000100
c. 0111011101110101
d. 010010010010
12. Th c hi n các s chuy n đ i d i đây. Trong s đó, có th th 1 cách t t nh t trong nhi uự ệ ố ể ổ ướ ố ể ử ố ấ ề
cách đã kh o sát. ả
a. (1417)10 = (……………………….……..)2
b. (-255)10 = (………………………………)2
c. (1110101000100111)2 =(……………………………)10
e. (2497)10 = (……………………………..)8
g. (235)8 = (……………………………)10
i. (7A9)16 = (…………………………….)10
k. (1600,123)10 = (………………………………………)16
m. (865)10 =( …………………………………….)BCD
n. (100101000111)BCD = (……………………………….)10
Bài T p Đi n T S - Page ậ ệ ử ố 1
Bài t p ch ng 2ậ ươ
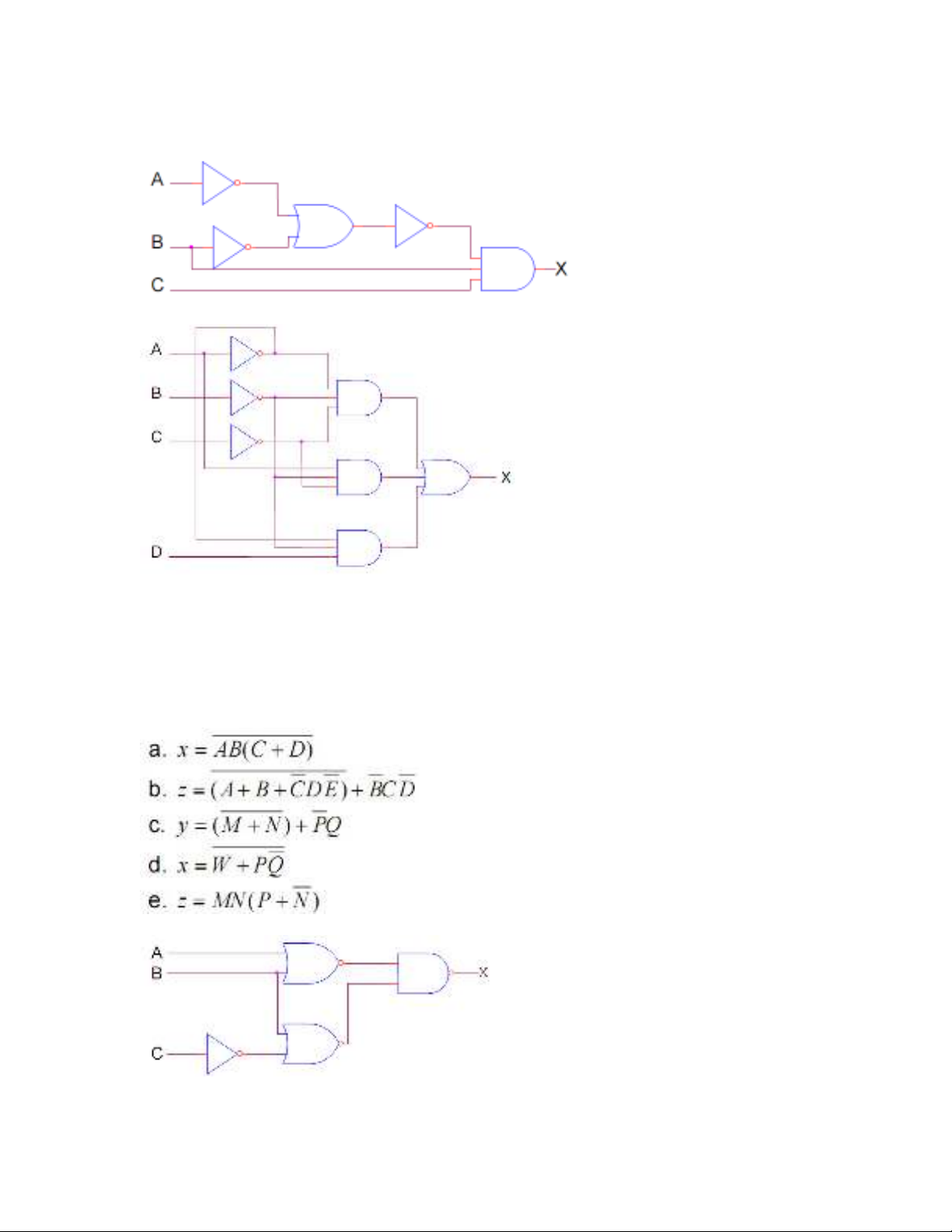
1. Vi t bi u th c Boolean cho ngõ ra X. Xác đ nh giá tr cu X ng v i các đi u ki n ngõ vàoế ể ứ ị ị ả ứ ớ ề ệ
có th và li t kê các giá tr vào b ng s th t.ể ệ ị ả ự ậ
(a)
(b)
2. Xác đ nh b ng s th t đ y đ cho m ch bài 1.b b ng cách tìm m c logic hi n di n t iị ả ự ậ ầ ủ ạ ở ằ ứ ệ ệ ạ
ngõ ra ng v i m i s k t h p c a ngõ vào.ứ ớ ỗ ự ế ợ ủ
Thay c ng OR thành c ng AND, c ng AND thành c ng OR bài 1, vi t bi u th c ngõ ra. ổ ổ ổ ổ ở ế ể ứ
3. ng v i m i bi u th c bên d i, xây d ng m ch logic t ng ng, dùng c ng AND, OR,Ứ ớ ỗ ể ứ ướ ự ạ ươ ứ ổ
c ng đ o.ổ ả
4. Vi t bi u th c ngõ ra cho m ch sau và xác đ nh b ng s th tế ể ứ ạ ị ả ự ậ
5. Thay đ i m ch đi n đ c xây d ng trong bài 4 ch dùng c ng NAND .ổ ạ ệ ượ ự ỉ ổ
Bài T p Đi n T S - Page ậ ệ ử ố 2
6. Hoàn t t các bi u th c sauấ ể ứ
a. A + 1 =
b. A . A =
c. B .
B
=
d. C + C =
e. X . 0 =
f. D . 1 =
g. D + 0 =
h. C +
C
=
i. G + GF =
j. y +
w
y =
7. Đ n gi n các bi u th c sauơ ả ể ứ :
8. Đ n gi n các bi u th c bên d i dùng đ nh lý DeMorgan:ơ ả ể ứ ướ ị
Bài T p Đi n T S - Page ậ ệ ử ố 3
Bài t p ch ng 3ậ ươ
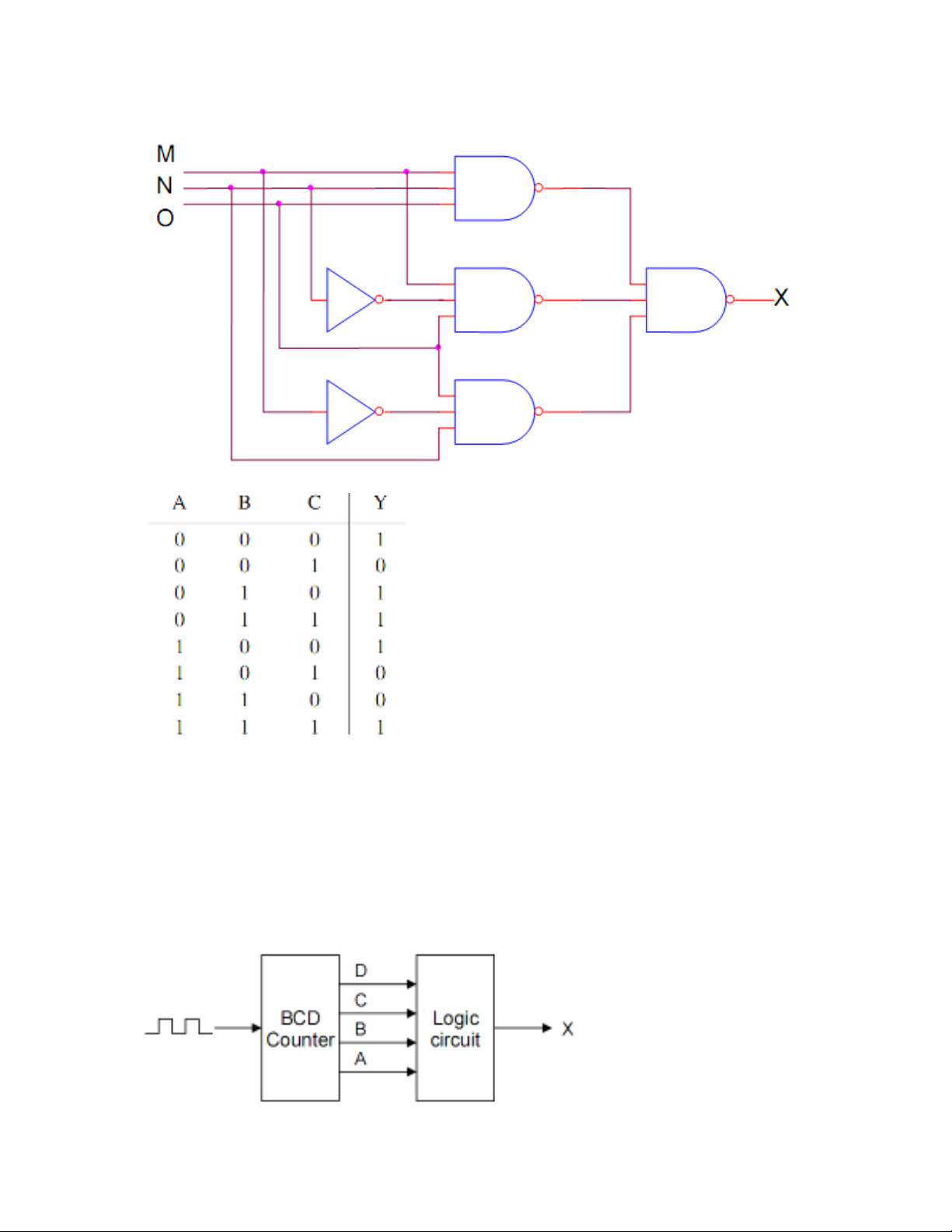
3.1. Đ n gi n m ch sau dùng đ i s Booleanơ ả ạ ạ ố
3.2. Thi t k m ch đi n logic t ng ng v i b ng s th t sau:ế ế ạ ệ ươ ứ ớ ả ự ậ
3.3. Thi t k m ch đi n logic có 3 ngõ vào A, B và C. Ngõ ra m c HIGH ch khi có 2 ngõế ế ạ ệ ở ứ ỉ
vào là m c LOW.ứ
3.4. M t s nh phân 4 bit có ký hi u là Aộ ố ị ệ 3 A2 A1 A0, v i Aớ0 là bit LSB, thi t k m ch logicế ế ạ
mà ngõ ra m c HIGH khi các s nh phân l n h n 0010 và nh h n 1000.ở ứ ố ị ớ ớ ỏ ơ
3.5. Th c hi n m ch đi n bài 3.3 dùng t t c là c ng NAND ự ệ ạ ệ ở ấ ả ổ
3.6. Th c hi n m ch đi n bài 3.4 dùng t t c là c ng NAND ự ệ ạ ệ ở ấ ả ổ
3.7. M t b đ m BCD v i ngõ ra 4 bit mã BCD hi n th s xung đ c đ a vào b đ m. Thíộ ộ ế ớ ể ị ố ượ ư ộ ế
d , sau 4 xung, ngõ ra c a b đ m là DCBA = 0100ụ ủ ộ ế 2 = 410. B đ m Reset v 0000 t i xungộ ế ề ạ
th 10 và b t đ u đ m l i t đ u. Nói cách khác, ngõ ra DCBA không bao gi bi u di n giáứ ắ ầ ế ạ ừ ầ ờ ể ễ
tr l n h n 1001ị ớ ơ 2 = 910. Hãy thi t k m ch logic v i ngõ ra m c HIGH khi đ m s 2, 3, 9.ế ế ạ ớ ở ứ ế ố
Bài T p Đi n T S - Page ậ ệ ử ố 4
3.8. Hình sau bi u di n 4 công t c trong m ch đi u khi n máy copy. Thông th ng các côngể ễ ắ ạ ề ể ườ
t c này m (open). Khi có gi y đi qua công t c thì đóng (close). Công t c 1 và 4 không thắ ở ấ ắ ắ ể
đóng (close) t i cùng 1 th i đi m. Hãy thi t k 1 m ch logic v i ngõ ra m c HIGH khi 2ạ ờ ể ế ế ạ ớ ứ
công t c hay nhi u h n cùng đóng.ắ ề ơ
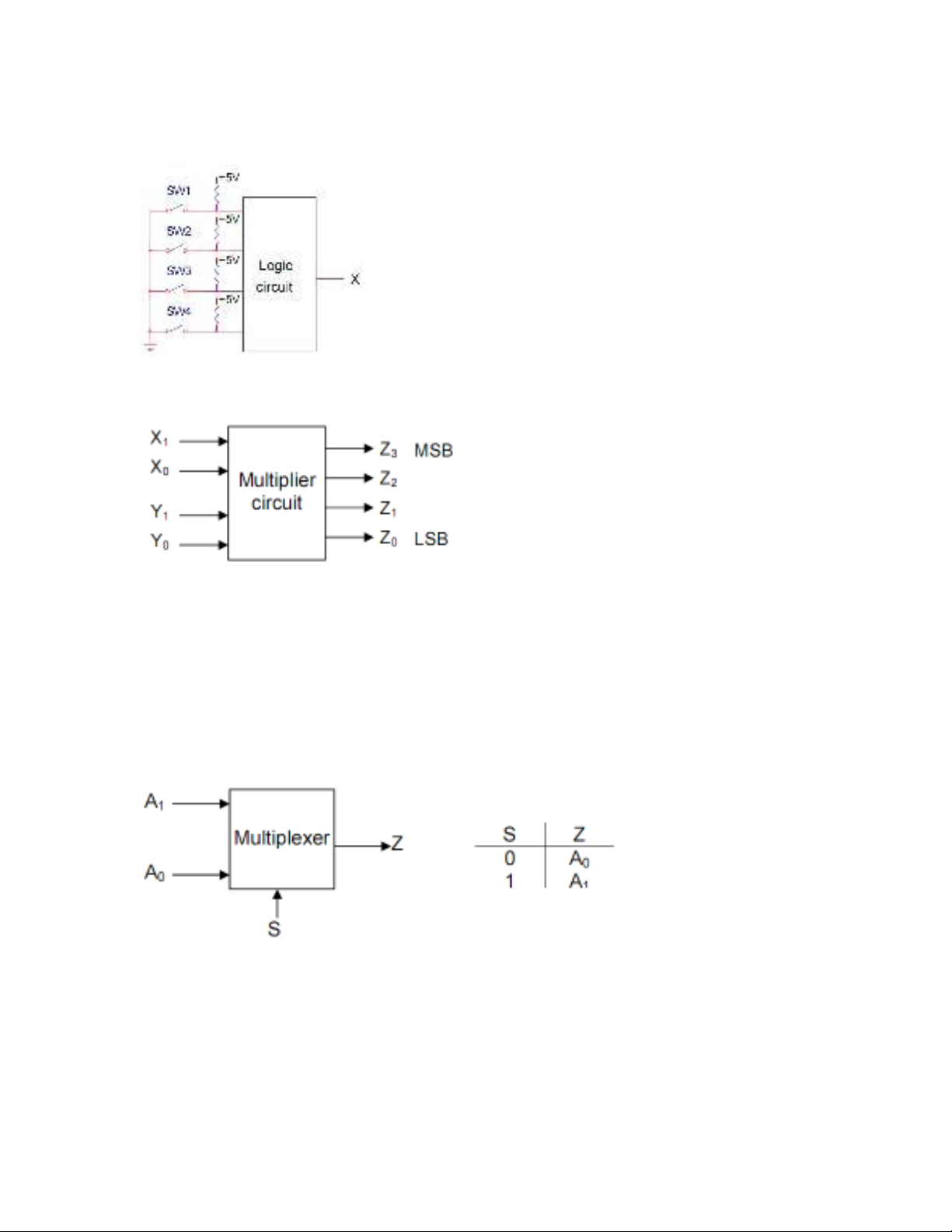
3.9. Hình sau th hi n m ch nhân hai s nh phân 2 bit xể ệ ạ ố ị 1x0 và y1y0 , ngõ ra là s nh phânố ị
z3z2z1z0 t ng ng v i tích đ i s c a 2 s ngõ vào. Hãy thi t k m ch logic cho m chươ ứ ớ ạ ố ủ ố ế ế ạ ạ
nhân.
3.10. M t mã BCD đ c truy n t i thi t b nh n t xa, các bit là Aộ ượ ề ớ ế ị ậ ừ 3A2A1A0, v i Aớ3 là bit
MSB. M ch nh n g m 1 m ch phát hi n l i BCD đ ki m tra mã nh n. Thi t k m chạ ậ ồ ạ ệ ỗ ể ể ậ ế ế ạ
ki m tra t o m c HIGH n u có b t kỳ đi u ki n l i nào x y ra. ể ạ ứ ế ấ ề ệ ỗ ả
3.11. Thi t k m ch logic v i đi u ki n: tín hi u ngõ vào A đ n ngõ ra Y ch khi ngõ vàoế ế ạ ớ ề ệ ệ ế ỉ
đi u khi n B m c LOW và ngõ vào đi u khi n C m c HIGH, các tr ng h p còn l iề ể ở ứ ề ể ở ứ ườ ợ ạ
ngõ ra m c LOW. ứ
3.12. Thi t k m ch logic đi u khi n s đi qua c a 1 tín hi u A theo các yêu c u sau: ế ế ạ ề ể ự ủ ệ ầ
a. Ngõ ra X = A khi ngõ vào đi u khi n B và C gi ng nhau. ề ể ố
b. X duy trì m c HIGH khi B và C khác nhau. ứ
3.13. Thi t k m ch logic có yêu c u cho hình sau. ế ế ạ ầ ở
3.14. Cho hàm Boolean sau: Y = ΠDCBA (3, 5, 6,11,12,13,14,15) + d(4,7,8,9)
a). Rút g n hàm Y, bi u di n hàm Y dùng c ng logic ọ ể ễ ổ
b). Th c hi n hàm Y dùng MUX 8 sang 1 (74LS151)ự ệ
3.16. Cho hàm Boolean sau: Y = ∑ ABC(0,1,4) + d(3,6)
a). Rút g n hàm Y, bi u di n hàm Y dùng c ng logic ọ ể ễ ổ
b). T hàm Y rút g n, bi n đ i l i m ch logic dùng toàn c ng NAND ừ ọ ế ổ ạ ạ ổ
c). Th c hi n hàm Y dùng gi i mã 3 sang 8 (74LS138)ự ệ ả
Bài T p Đi n T S - Page ậ ệ ử ố 5