BÀI T P MÔN S C B N V T LI UẬ Ứ Ề Ậ Ệ
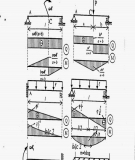
Bài 1 V bi u đ n i l c, ng su t,ẽ ể ồ ộ ự ứ ấ
chuy n vi c a các m t c t ngangể ủ ặ ắ
c a thanh ch u l c nh hình.ủ ị ự ư
P.án (1) (2) (3) (4) (5) (6) (7) (8)
1EF 2EF P P a a a 3a
2EF 2EF 2P P 2a a a a
3EF 2EF P 2P a 2a a a
42EF 1EF P P a 2a a a
5EF 2EF 2P P a a 2a a
6EF 2EF P P 2a a a a
7EF 2EF P 3P a a 2a a
8EF 2EF 2P P 3a a a a
93EF 2EF P 2P a a a a
10 EF 2EF 2P P a a 2a 2a
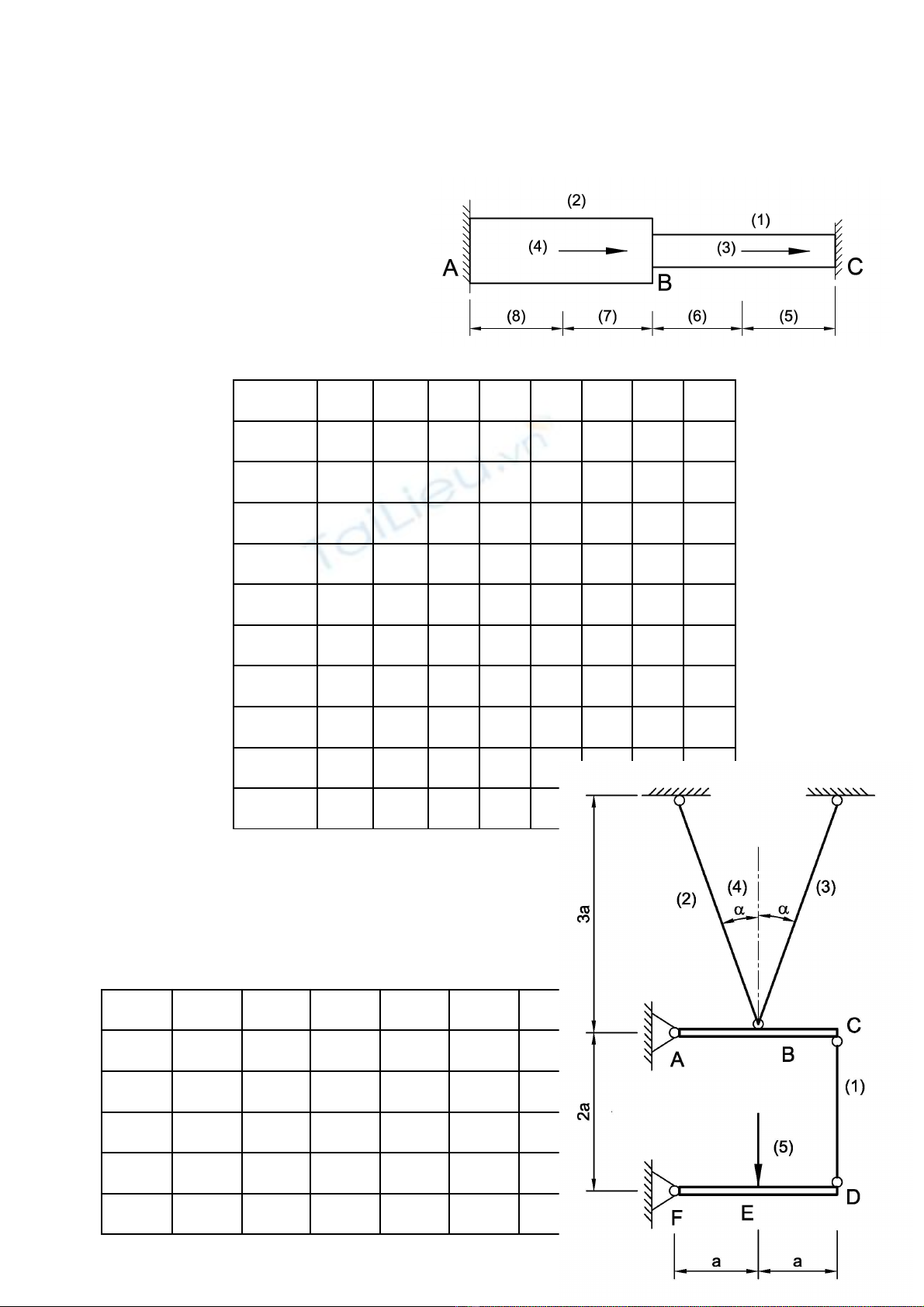
Bài 2 Cho h ch u l c nh hình v , các thanh AC,ệ ị ự ư ẽ
DF tuy t đ i c ng. Xác đ nh chuy n v th ng đ ngệ ố ứ ị ể ị ẳ ứ
t i đi m D theo P, E, F, a, ạ ể α
P.án 1 2 3 4 5 6 7 8 9 10
(1) EF EF 2EF EF EF 2EF EF 2EF EF 2EF
(2) 2EF EF EF 2EF 2EF EF 2EF 2EF EF EF
(3) 2EF EF EF 2EF 2EF EF 2EF 2EF EF EF
(4) 300450600450300300600300300450
(5 2P P P P 2P P P 2P P P
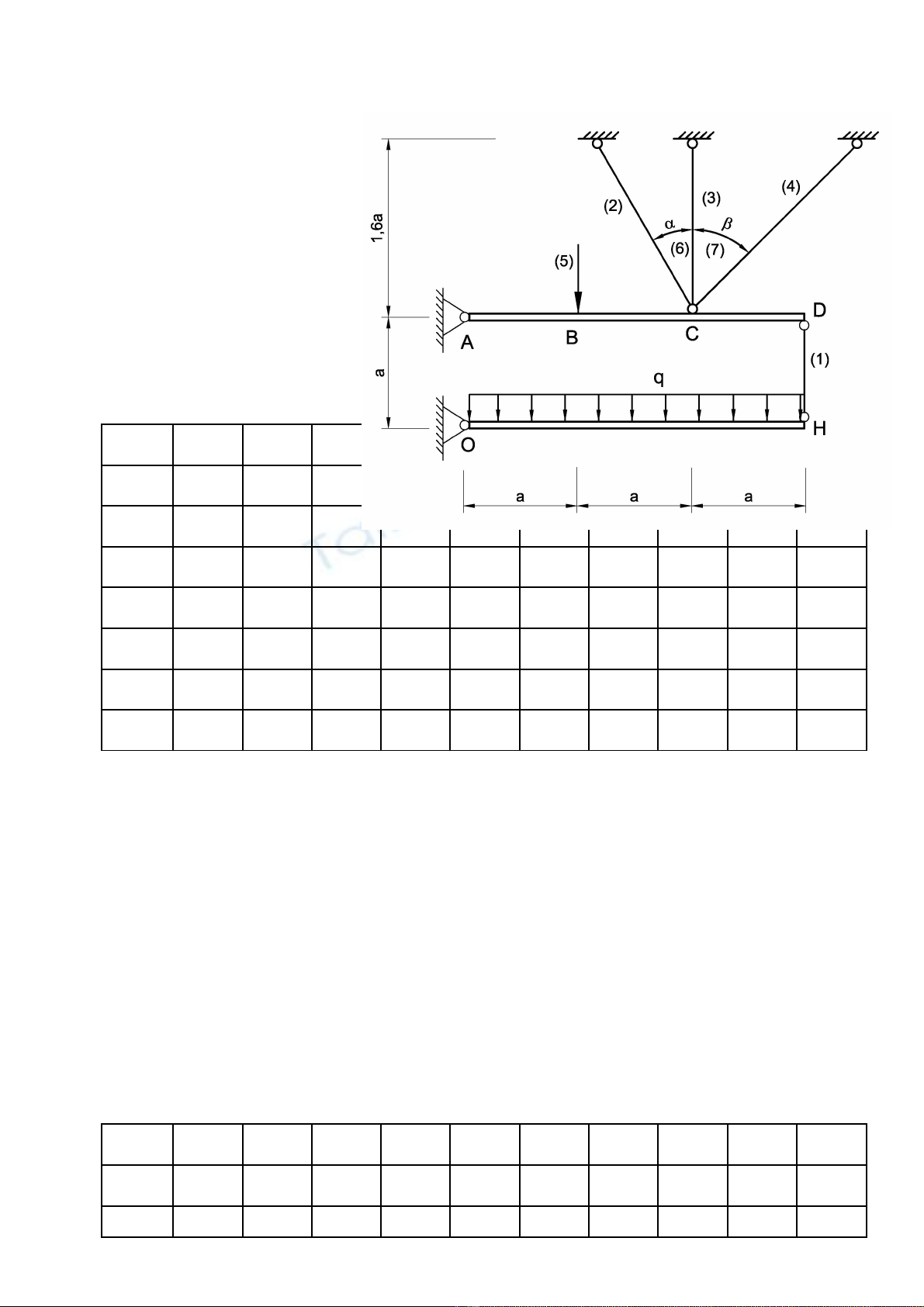
Bài 3 Cho h g m hai thanh AD và OH tuy t đ i c ng đ c treo b i các thanh đàn h iệ ồ ệ ố ứ ượ ở ồ
làm t m t lo i v t li u.ừ ộ ạ ậ ệ
Tinh ng su t trong cácứ ấ
thanh và đ d ch chuy nộ ị ể
c a đi m H. Cho P=qaủ ể
P.án 1 2 3 4 5 6 7 8 9 10
(1) EF 2EF EF EF EF 2EF EF EF EF 2EF
(2) EF EF 2EF EF EF EF EF EF EF EF
(3) 2EF 2EF EF 2EF 2EF 2EF 2EF 2EF 2EF EF
(4) 2EF 2EF 2EF EF 2EF 2EF 2EF 2EF 2EF 2EF
(5) P 2P P P P P P P 2P P
(6) 300300450300300450300300300300
(7) 450450450300450450450300450450
Bài 4 Xác đ nh ng su t trên m t c t ngang các thanh có môđun đàn h i E, di n tíchị ứ ấ ặ ắ ồ ệ
m t c t ngang F và chuy n v c a đi m đ t l c.ặ ắ ể ị ủ ể ặ ự
P.án 1 2 3 4 5 6 7 8 9 10
(1) P P P P 2P 2P 2P 2P P P
(2) 600300600450600300600450600450
(3) 300300600450300300600450450300
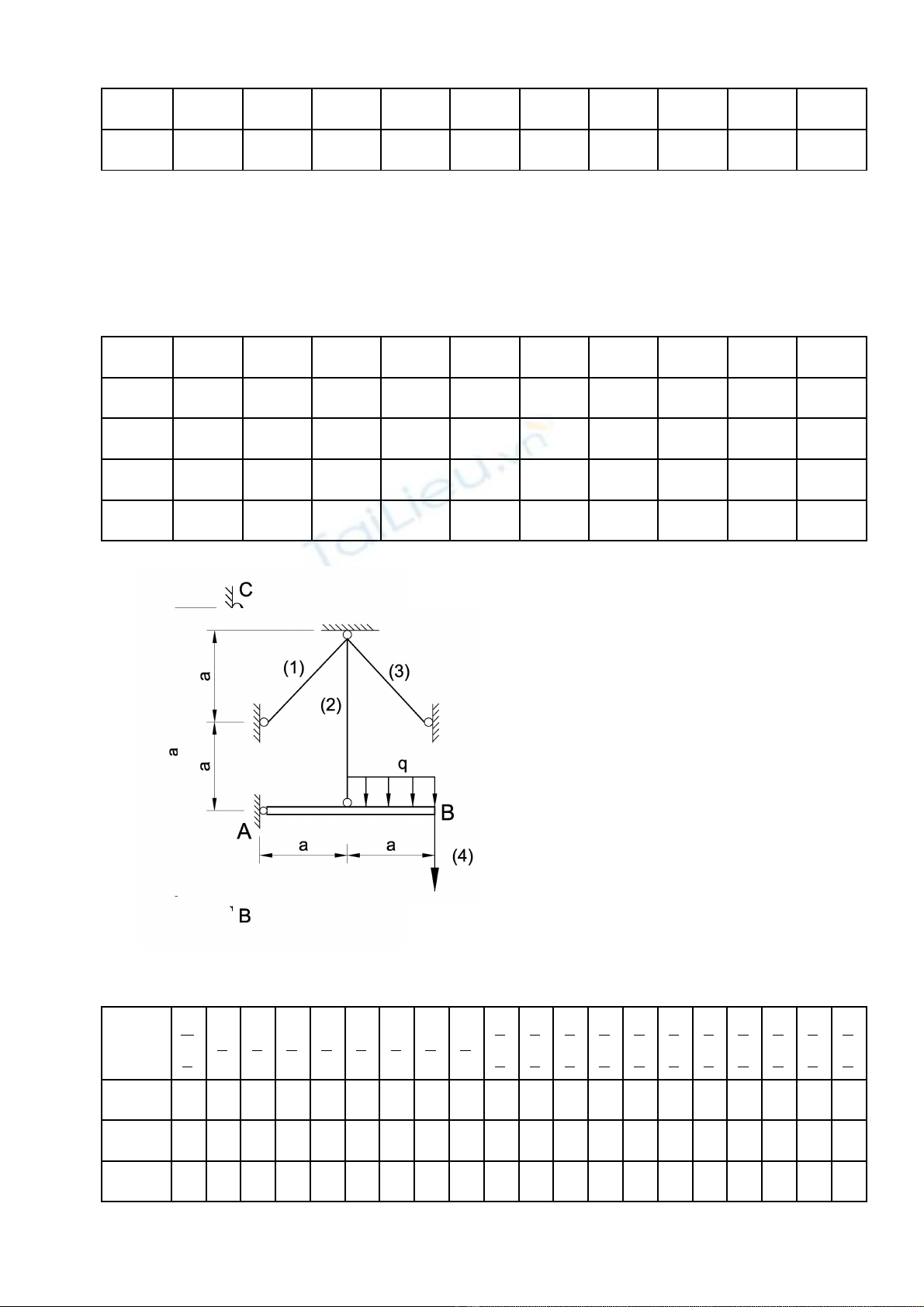
Bài 5 Thanh tuy t đ i c ng AB n i kh p t i A và gi cân b ng b i các thanh (1), (2), (3)ệ ố ứ ố ớ ạ ữ ằ ở
làm b ng thép. Xác đ nh di n tích F t i thi u đ m b o h làm vi c an toàn, P=qaằ ị ệ ố ể ả ả ệ ệ
P.án 1 2 3 4 5 6 7 8 9 10
(1) EF 2EF EF EF EF 3EF 2EF 2EF 4EF 3EF
(2) EF 2EF EF EF EF 3EF 2EF 2EF 4EF 3EF
(3) EF 2EF EF EF EF 3EF 2EF 2EF 4EF 3EF
(4) P P 2P 4P 3P 2P 2P 3P 4P 4P
PHÂN NHÓM BÀI T P SBVLẬ
Nhóm B
1
23456789
1
0
1
1
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
2
0
11 1 1 1
22222
33333

44 4 4 4
55555
66 6 6 6
77 7 7 7
88 8 8 8
99999
10 0 0 0 0
11 2 4 5 7
12 3 5 7 9
13 14684
14 1 4 3 5
15 3 3 4 6