
Bài t p Ch ng haiậ ươ
BT 2.1. S d ng công th c đ nh nghĩa đ tìm ử ụ ứ ị ể
)(z
i
X
và
)]([ z
i
XRC
:
1.
)()( 1
1−= nuanx n
4.
)()( 1
4−= nbnx n
δ
2.
)()(
2nunx −=
5.
)()( 1
5+= nbnx n
δ
3.
)()()( 1
3nunuanx n−−−=
6.
)()()( 11
6−+−= nuanbnx nn
δ
BT 2.2 S d ng các tính ch t c a bi n đ i ử ụ ấ ủ ế ổ Z đ tìm ể
)(z
i
X
và
)]([ z
i
XRC
:
1.
)()( 2
1−= nuanx n
4.
)(.)(
4nuannx n−= −
2.
)()(
2nuanx n−
=
5.
)()()( 2
5−−= −nuanuanx nn
3.
)()(
3nuanx n−= −
6.
)(*)()( 2
6−= −nnuanx n
δ
BT 2.3 Hãy tìm bi n đ i ế ổ Z thu n và mi n h i t c a các dãy sau :ậ ề ộ ụ ủ
1.
)()( 2
1−= nrectnx N
4.
)(.)(
4nrectannx N
n
=
2.
)()(
2nrectanx N
n
=
5.
N
nrectanx n)()(
5−=
3.
)(.)(
3nrectnnx N
=
6.
)(*)()( 2
6−= nrectnunx N
BT 2.4 Hãy tìm các hàm g c nhân qu sau b ng ph ng pháp th ng d :ố ả ằ ươ ặ ư
1.
2
1)).((
)(
5,01
52
+−
+
=zz
z
zX
2.
21
21
1
)( −− +−
=zz
zX
BT 2.5 Hãy tìm các hàm g c nhân qu và ph n nhân qu c a các hàm nh ố ả ả ả ủ ả Z sau b ngằ
ph ng pháp khai tri n thành chu i lu th a :ươ ể ỗ ỹ ừ
1.
2
)(
1+
=z
z
zX
2.
2
2
)(
)(
1
−
=z
z
z
X
BT 2.6 Hãy tìm các hàm g c nhân qu c a các hàm nh ố ả ủ ả Z sau :
1.
2
2
1)(
)(
)(
1
1
−
+
=z
z
zX
3.
21
1
3521
21
)( −−
−
+−
−
=zz
z
zX
2.
)(
)(
)(
1
1
2
2
2−
+
=z
z
zX
4.
2
4))((
)(
312
32
−+
+
=zz
z
zX
BT 2.7 Hãy tìm các hàm g c ph n nhân qu c a các hàm nh ố ả ả ủ ả Z sau :
1.
2
2
1)(
)(
)(
1
1
−
+
=z
z
zX
2.
21
1
2521
21
)( −−
−
+−
−
=zz
z
zX
BT 2.8 Hãy tìm các hàm g c nhân qu c a các hàm nh ố ả ủ ả Z sau :
1.
)(
)(
2
1
3
1+
=−
−
z
z
zX
3.
2
3
3))((
)(
1312
18
−−
=zz
z
zX
2.
)(
)(
12
4
3
2+
+
=zz
z
zX
4.
)(
)(
125,332
84
2
2
4+−
+
=zz
zz
zX
BT 2.9 Xác đ nh ph n ng ị ả ứ y(n) và tính n đ nh c a ổ ị ủ h x lý s có đ c tính xungệ ử ố ặ
)()( 35,0 −= nunh n
và tác đ ng ộ
)cos()()( .3.2 nnunx =
.
BT 2.10 Cho h x lý s có ph ng trình sai phân ệ ử ố ươ
)()()( 23 nxnyny =−−
1. Tìm hàm h th ng ệ ố H(z) và xác đ nh tính n đ nh c a h .ị ổ ị ủ ệ
2. Tìm đ c tính xung ặh(n) c a h .ủ ệ
3. V i tác đ ng ớ ộ
)()( 23 −= nunx n
, hãy tìm ph n ng ả ứ y(n) c a h .ủ ệ
BT 2.11 Cho h x lý s có đ c tính xung ệ ử ố ặ
)().()( 12 nunh n−=
. Hãy tìm tác đ ng ộx(n) để
h làm vi c n đ nh.ệ ệ ổ ị
BT 2.12 Hãy xác đ nh tính n đ nh c a các h x lý s ị ổ ị ủ ệ ử ố TTBBNQ sau :
1.
)(
)( 21
21
1352
23
−−
−−
−+
+−
=zz
zz
zH
2.
)(
)(
4103
26
2
2++
+
=zz
z
zH
BT 2.13 Hãy xác đ nh tính n đ nh c a các h x lý s ị ổ ị ủ ệ ử ố TTBBNQ sau :
1.
)(
)( 321
3
12586
1
−−−
−
−−+
−
=zzz
z
zH
117
2.
)(
)(
1375,1129
35
234
2
2−++−
−+
=zzzz
zz
zH
BT 2.14 Tìm ph n ng ả ứ y(n) và xét tính n đ nh c a h x lý s có ph ng trình saiổ ị ủ ệ ử ố ươ
phân
)()()()()( 23275,113 −+−−−−= nxnxnynyny
, v i ớtác đ ng ộ
)()( 13 −= nunx n
, và đi uề
ki n đ u ệ ầ
12)( =−y
,
21)( =−y
.
BT 2.15 Hãy gi i ph ng trình sai phân ả ươ
)()()( 13,0 −+= nynxny
với tác đ ngộ
).sin()()( 3,03 nnunx
π
=
và đi u ki n ban đ u b ng không. Xác đ nh dao đ ng t doề ệ ầ ằ ị ộ ự
y0(n) và dao đ ng c ng b c ộ ưỡ ứ yp(n) .
BT 2.16 Hãy gi i ph ng trình sai phân ả ươ
)()()( 134 −+= nynxny
với tác đ ngộ
).cos()()(
5,03
nnunx
n
π
−
=
và đi u ki n ban đ u b ng không. Xác đ nh dao đ ng t doề ệ ầ ằ ị ộ ự
y0(n) và dao đ ng c ng b c ộ ưỡ ứ yp(n).
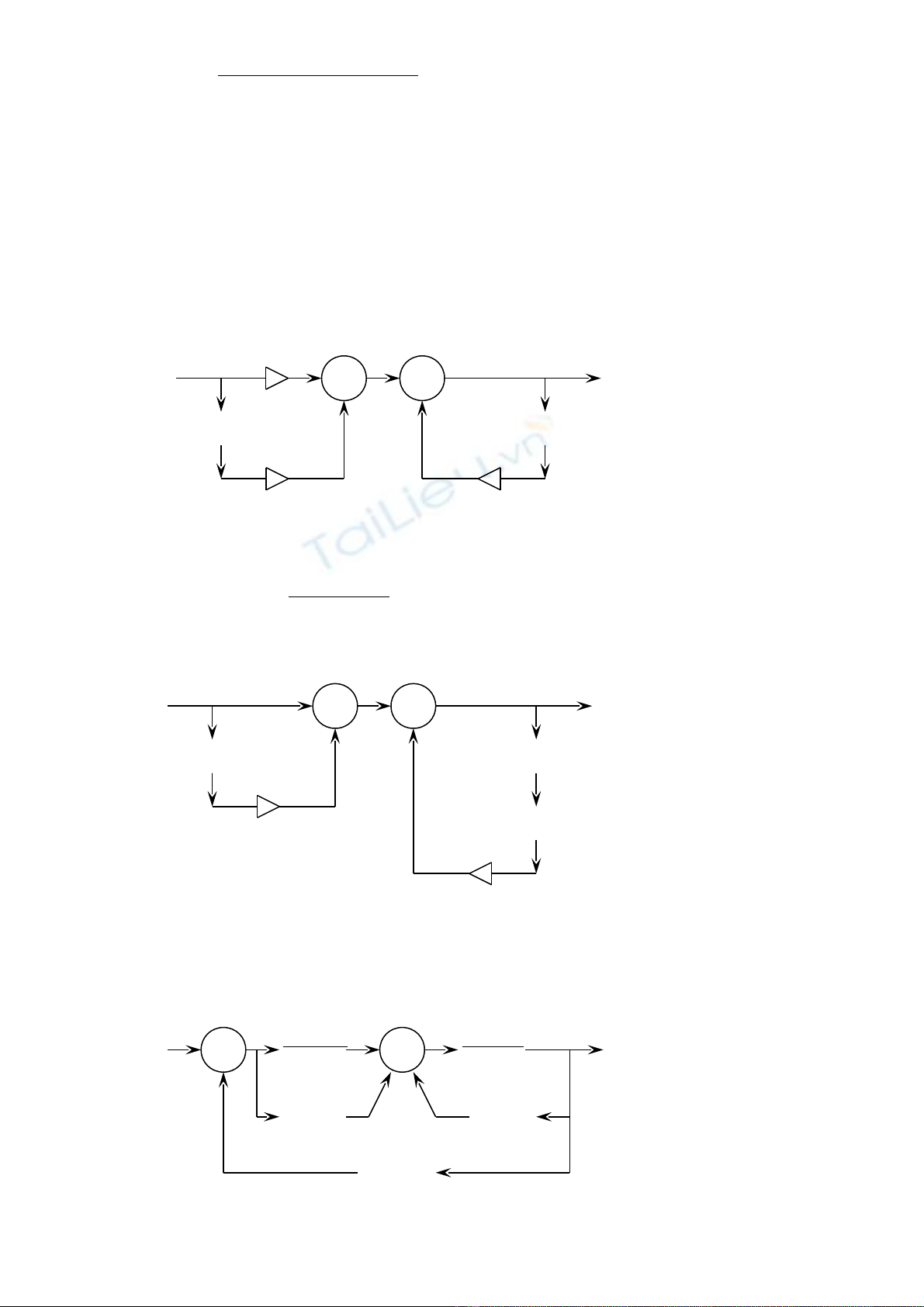
BT 2.17 Tìm đ c tính xung ặh(n) c a h x lý s ủ ệ ử ố TTBBNQ có s đ c u trúc trên hìnhơ ồ ấ
2.20, và xét tính n đ nh c a h .ổ ị ủ ệ
Hình 2.20 : Sơ đồ cấu trúc hệ xử lý số của BT 2.17.
BT 2.18 Hãy xây d ng s đ c u trúc c a h x lý s có hàm h th ng là : ự ơ ồ ấ ủ ệ ử ố ệ ố
).(
)(
32
3
2−+
=zzz
zH
BT 2.19 Cho h x lý s ệ ử ố TTBBNQ có s đ c u trúc trên hình ơ ồ ấ 2.21, tìm ph n ng ả ứ y(n)
c a h khi tác đ ng ủ ệ ộ
)sin()()( .5.2 nnunx n−
=
Hình 2.21 : Sơ đồ cấu trúc hệ xử lý số của BT 2.19.
BT 2.20 Tìm hàm h th ng ệ ố H(z) và xét tính n đ nh c a h x lý s có s đ kh iổ ị ủ ệ ử ố ơ ồ ố
trên hình 2.22.
Hình 2.22 : Sơ đồ khối của hệ xử lý số ở BT 2.20.
118
0,5
X(z) Y(z
)
+
3+
2
1
−
z
1
−
z
X(z) Y(z
)
++
-2
1
−
z
0,5
1
−
z
1
−
z
X(z
)
Y(z
)
+ +
25
10
+
z
1
2,0
−
−
z
12
4
−
z
1
2
−
−
z

BT 2.21 Tìm hàm t ng quan ươ
)(mr
xy
c a dãyủ
)()( nuanx
n
=
v i các dãy : ớ
1.
)()(
1
nuny =
3.
)()(
4
nrectny
N
=
2.
)()(
2
nuany
n
−
=
4.
)()(
5
nny
δ
=
BT 2.22 Hãy xác đ nh hàm t t ng quan ị ự ươ
)(mr
x
c a các dãy sau :ủ
1.
)()(
1
nunx
=
3.
)()(
3
nrectnx
N
=
2.
)()(
2
nuanx
n
=
4.
)()(
4
nrectanx
N
n
=
119
























