Bài t p Ch ng baậ ươ
BT 3.1 V i |ớa| < 1 , hãy xác đ nh s t n t i và tìm bi n đ i ị ự ồ ạ ế ổ Fourier c a các dãyủ
sau :
1.
)()(
1nuanx n
=
5.
).sin().()( 05 nnunx
ω
=
2.
)()(
2nuanx n−
=
6.
).sin().()( 06 nnuanx n
ω
=
3.
)()(
3nuanx n−=
7.
).cos().()( 07 nnunx
ω
=
4.
)()(
4nuanx n−= −
8.
BT 3.2 Xác đ nhị các hàm ph n th c và ph n o, mô đun và argumen c a các hàm t n sầ ự ầ ả ủ ầ ố
sau :
1.
3.
ω
ω
ω
j
j
j
e
e
eX−
−
−
=.25,01
)(
3
2.
ωω ω
−
=ee j
X).sin()( 2
2
4.
)(
4.)( 3
ωαω
jj eeX+−
−=
BT 3.3 Cho dãy
−∉
−∈
=],[
],[
)( 0
1
NN
NN
nkhi
nkhi
nx
1. Xác đ nh ị
)(,)(,)(,)(,)(,)(,)(
ωθωϕωω ωωω
jj
IR
jeee AXXXX
2. V đ th c a ẽ ồ ị ủ x(n) ,
v i ớN = 2
BT 3.4 Tìm bi n đ i ế ổ Fourier ng c c a các hàm t n s sau :ượ ủ ầ ố
1.
ωω
5,0
)( jj eeX−
=
3.
ω
ω
2
cos)( =
j
eX
2.
ωω ω
5,0
)sin()( 2jj eeX−
=
4.
ωω ω
5,0
).cos()( 2jj eeX−
=
BT 3.5 Cho
ω
j
ea
nxFT −
−
=.
])([
1
1
, tìm bi n đ i ế ổ Fourier c a các dãy sau :ủ
1.
)()( 2
1+= nxnx
4.
)()()( 22
4−++= nxnxnx
2.
)()(
2
nxnx −=
5.
)()( 2
5,1
5−= nxenx nj
3.
)(*)()(
3nxnxnx −=
6.
)(.)( 2
6−= nxnnx
BT 3.6 Xác đ nh hàm ph c a các tín hi u s sau :ị ổ ủ ệ ố
1.
)()( 2
31 −= nrectnx
3.
)(*)()( 333 nrectnrectnx −=
2.
)()( 32 nrectnx −=
4.
)()()( 12
34 −+−= nnrectnx
δ
BT 3.7 Xác đ nh hàm truy n đ t ph c ị ề ạ ứ H(ej
ω
) c a các h x lý s sau :ủ ệ ử ố
1.
∑
∞
=
−−=
0
)()( 3
k
kknxny
3.
∑
−
=
−= 1
0
)()( 2
N
k
kknxny
2.
)()()( 122 −−−= nnxny y
4.
)()()( 12 −−= nxnxny
BT 3.8 H x lý s có đ c tính xung ệ ử ố ặ
)()( 1
2−= nrectnh
, hãy tìm ph n ng ả ứ y(n), hàm
ph ổY(ej
ω
) và các đ c tr ng ph c a ặ ư ổ ủ y(n), khi tác đ ng vào h làộ ệ
)()( 13 −= −nunx n
BT 3.9 H x lý s có ệ ử ố ph n ng ả ứ
)()()( 1.5,022.2 2−−−= −nrectnuny n
và tác đ ngộ
)()( 12 −= −nunx n
, hãy xác đ nh hàm truy n đ t ph c ị ề ạ ứ H(ej
ω
), đ c tính xung ặh(n) và
các đ c tính t n s c a ặ ầ ố ủ hệ.
BT 3.10 Tìm H(ej
ω
) , H(ej
ω
) và
ϕ
(
ω
) c a h x lý s có ph ng trình sai phân :ủ ệ ử ố ươ
)()()()()()( 4
24
1
3
6
1
2
2
1
1−+−+−+−+= nxnxnxnxnxny
BT 3.11 Tìm H(ej
ω
) , H(ej
ω
) và
ϕ
(
ω
) c a h x lý s có ph ng trình sai phânủ ệ ử ố ươ
)()()( Nnxnxny −+=
, v i ớN là h ng s .ằ ố
BT 3.12 Cho h x lý s có đ c tính xung ệ ử ố ặ
)()(
2
)1(
nrectanh
n+
=
1. Xác đ nh đi u ki n t n t i và bi u th c c a ị ề ệ ồ ạ ể ứ ủ H(ej
ω
).
2. Hãy xác đ nh các đ c tính t n s ị ặ ầ ố H(ej
ω
) và
ϕ
(
ω
) c a h .ủ ệ
3. V các đ th đ c tính biên đ t n s và pha t n s c a h . ẽ ồ ị ặ ộ ầ ố ầ ố ủ ệ
BT 3.13 Hãy xác đ nh hàm truy n đ t ph c, xác đ nh và v d ng c a đ c tính biên đị ề ạ ứ ị ẽ ạ ủ ặ ộ
t n s , đ c tính pha t n s c a các h x lý s sau :ầ ố ặ ầ ố ủ ệ ử ố
1. Trên hình 3.11.
142
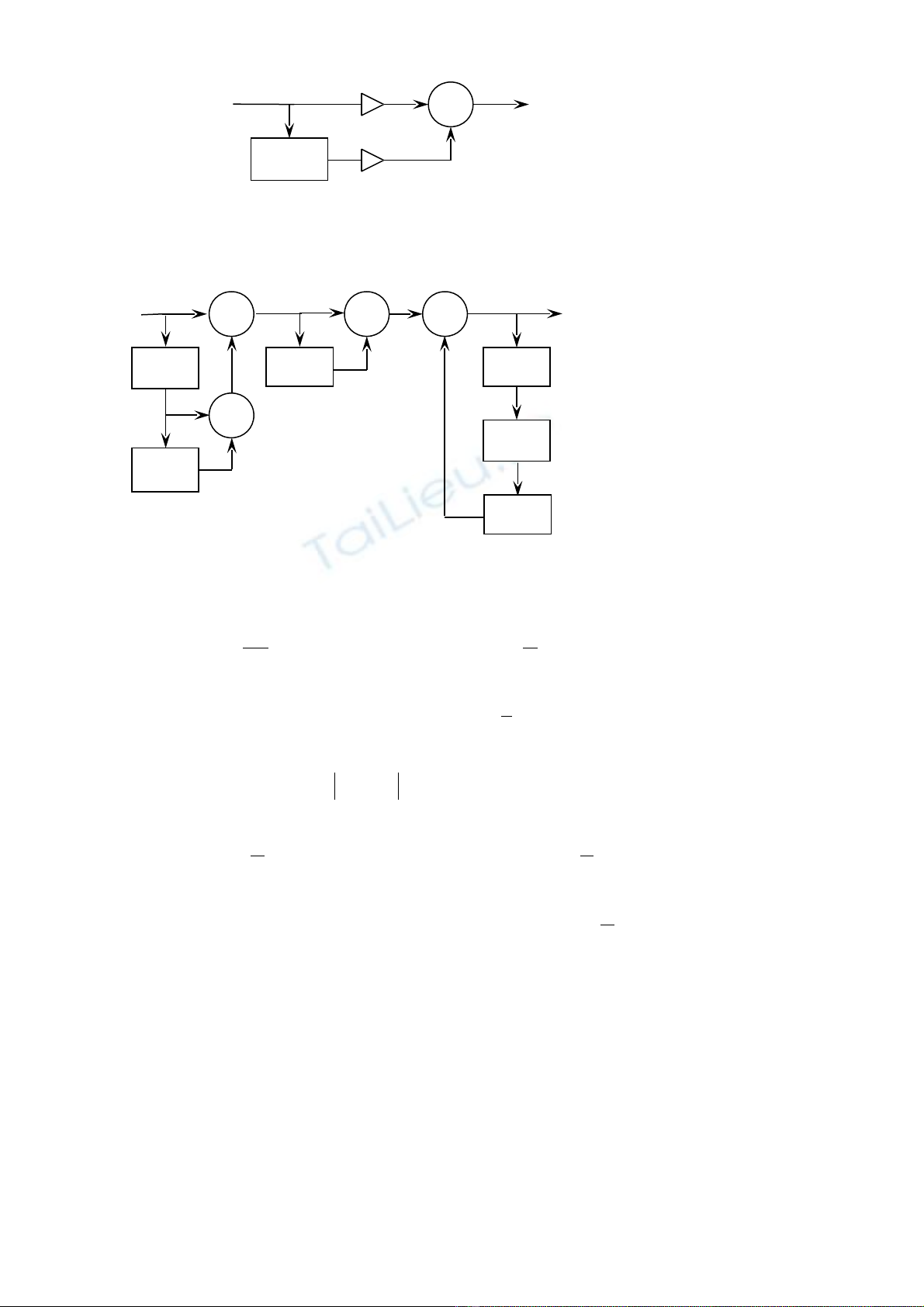
2. Trên hình 3.12.
Hình 3.11 : Sơ đồ cấu trúc của hệ xử lý số ở BT3.13.1
Hình 3.12 : Sơ đồ cấu trúc của hệ xử lý số ở BT3.13.2
BT 3.14 Hãy xác đ nh các đ c tr ng ph c a các tín hi u s sau :ị ặ ư ổ ủ ệ ố
1.
)(.
.
cos)(
1nrect
n
nx N
N
=
π
2.
BT 3.15 Hãy tính năng l ng c a các tín hi u s sau theo hàm ph :ượ ủ ệ ố ổ
1.
)(.)( 21 2nrectnx n
=
2.
)(.)( 32 1
2nrect
n
nx
−=
BT 3.16 Cho các tín hi u s ệ ố
)()(
2
nunx
n
−
=
và
)(.)(
2
2
nrectny
n
=
, hãy tìm hàm phổ
[ ]
)()( mrFTe xy
j
xy
R=
ω
,
)(
ω
j
xy eR
,
[ ]
)(
ω
j
xy eArg R
.
BT 3.17 Hãy tìm hàm ph ổ
)(
ω
j
xeR
c aủ các tín hi u s sau :ệ ố
1.
)(.sin)(
41
2
nrectnnx
=
π
2.
)(.cos)( 42 2nrectnnx
=
π
BT 3.18 Tìm đ c tính xung ặh(n) c a các h x lý s có đ c tính t n s : ủ ệ ử ố ặ ầ ố
1.
π
πω
ω
5,0
)cos()( jj eeH−=
2.
ωω ω
5,0
2
2sin)( jj eeH
=
BT 3.19 Cho tín hi u liên t c ệ ụ x(t) có ph h u h n ổ ữ ạ
Hzf 3500<
:
≥
<
=−0
00
)( tkhi
tkhi
tx t
eA
α
1. Xác đ nh chu kỳ trích m u l n nh t ị ẫ ớ ấ T đ ph c a tín hi u l y m uể ổ ủ ệ ấ ẫ
x(nT) không b méo d ng so v i ph c a ị ạ ớ ổ ủ x(t) .
2. Hãy bi u di n ph ể ễ ổ
)(
ω
j
eX
c a ủx(nT) qua ph ổ
)(
ω
•
X
c a ủx(t).
BT 3.20 Hãy xây d ng s đ kh i và s đ c u trúc trong mi n t n s c a h s lýự ơ ồ ố ơ ồ ấ ề ầ ố ủ ệ ử
s có ph ng trình sai phân nh sau :ố ươ ư
)()()()()( 25,0122 −−−+−+= nxnnxnxny y
143
X(ej
ω
)+
e-j
ω
2
3
Y(ej
ω
)
X(ej
ω
)
Y(ej
ω
)
e-j
ω
+
e-j
ω
+
e -j
ω
e-j
ω
+
e-j
ω
e-j
ω
+