
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 5(114).2017-Quyển 1 81
HAI PHƯƠNG PHÁP THAY THẾ ĐỐI TƯỢNG CÓ TRỄ TRONG
BÀI TOÁN ĐIỀU KHIỂN TỐI ƯU HỆ CÓ THAM SỐ PHÂN BỐ
TWO METHODS REPLACE A DELAYED OBJECT IN OPTIMAL CONTROL PROBLEMS
FOR A DISTRIBUTED PARAMETER SYSTEM
Mai Trung Thái, Nguyễn Thị Mai Hương
Trường Đại học Kỹ thuật Công nghiệp, Đại học Thái Nguyên;
maitrungthai@gmail.com, maihuongnguyen79@gmail.com
Tóm tắt - Các đối tượng điều khiển có trễ thường gặp nhiều trong
các lĩnh vực khác nhau như trong công nghiệp, giao thông, vận tải,
quân sự… Thông thường khi thiết kế bộ điều khiển, nếu đối tượng
là khâu quán tính bậc nhất có trễ được xấp xỉ bằng hai khâu quán
tính bậc nhất, thì điều này thường dẫn đến sai số lớn nếu thời gian
trễ () là lớn đáng kể so với hằng số thời gian (). Bài báo nghiên
cứu so sánh độ chính xác của lời giải khi thay thế một đối tượng
động học có trễ bằng mô hình xấp xỉ Taylor và mô hình xấp xỉ Pade
bậc 1 để giải bài toán điều khiển tối ưu cho một hệ có tham số phân
bố, có trễ. Hệ này được áp dụng cho hệ thống truyền nhiệt một
phía trong lò gia nhiệt để điều khiển nhiệt độ cho phôi tấm theo tiêu
chuẩn nung chính xác nhất.
Abstract - The delayed control objects often happen in many
different fields such as industry, transport, transportation, military...
Normally, when designing the controller, if the object is the delayed
first order inertia system which is approximated by two systems of
the first order inertia, this often leads to the large error if the time
delay () is significantly large compared to its time constant (). This
paper presents a study comparing the accuracy of the solution
when replacing a delayed object by the Taylor and the first-order
Pade approximation models to solve the problem of optimal control
for a distributed parameter system with time delay (DPSTD). The
system is applied to a one-sided heat-transfer system in a heating
furnace to control temperature for a slab following the most
accurate burning standards.
Từ khóa - điều khiển tối ưu; hệ tham số phân bố; có trễ; phương
pháp số; xấp xỉ Taylor; xấp xỉ Pade.
Key words - optimal control; distributed parameter systems; delay;
numerical method; Taylor approximation; Pade approximation.
1. Đặt vấn đề
Phương pháp xấp xỉ Taylor và phương pháp xấp xỉ Pade
[1] đã được phát triển từ lâu và ứng dụng chủ yếu của nó là
để tìm nghiệm các phương trình đại số vi phân. Phương
pháp xấp xỉ Pade có thể cho ra phép xấp xỉ hàm có nhiều
ưu việt hơn so với phép khai triển Taylor, đặc biệt với
những đối tượng có thời gian trễ () lớn đáng kể so với
hằng số thời gian () của nó [5].
Bài báo đưa ra hai dạng thay thế cho đối tượng có trễ
bằng mô hình xấp xỉ Taylor và mô hình xấp xỉ Pade để giải
bài toán điều khiển tối ưu cho một hệ với tham số phân bố,
có trễ; điển hình cho đối tượng có trễ với tham số phân bố
là quá trình truyền nhiệt. Các thuật toán và kết quả mô
phỏng đã chỉ ra rằng, tùy theo mối quan hệ giữa () và ()
thì ta nên dùng dạng xấp xỉ nào là hợp lý nhất.
2. Đặt bài toán điều khiển tối ưu
2.1. Mô hình đối tượng
Xét hệ thống truyền nhiệt một phía trong lò gia nhiệt,
đó là một hệ có tham số phân bố. Quá trình đốt nóng một
phía cho phôi tấm trong lò gia nhiệt được mô tả bằng
phương trình đạo hàm riêng [2], [3], [4], [5]:
2
2
( , ) ( , )q x t q x t
at
x
(1)
Trong đó:
q(x,t) là phân bố nhiệt độ trong vật, phụ thuộc vào tọa
độ không gian x (0
x
) và thời gian t (0
t
T ), a là
hệ số dẫn nhiệt độ - thông số đặc trưng cho tốc độ biến
thiên nhiệt độ của vật (m2/s),
là bề dày tấm (m), T là thời
gian nung cho phép (s).
Các điều kiện đầu và điều kiện biên cho bởi [2], [3], [4],
[5]:
,0 0qx
(2)
0
,(0, ) ( )
x
q x t q t u t
x
(3)
,0
x
q x t
x
(4)
với
là hệ số trao đổi nhiệt giữa không gian lò và vật
(W/m2.độ);
là hệ số dẫn nhiệt của vật liệu (W/m.độ);
u(t) là nhiệt độ môi trường không khí trong lò (°C).
Quan hệ giữa công suất cung cấp cho lò w(t) và nhiệt
độ lò u(t) thường gặp là một khâu quán tính bậc nhất có trễ
[2], [5].
Khi đó quan hệ giữa w(t) và u(t) được mô tả bằng
phương trình:
() ( ) w( )
du t u t k t
dt
(5)
Trong đó:
là hằng số thời gian của lò (s);
là thời
gian trễ của lò (s); k là hệ số truyền tĩnh của lò; w(t) là công
suất cung cấp cho lò (hàm điều khiển của hệ thống).
Nhiệt độ u(t) của môi trường không khí trong lò được
điều khiển bởi công suất w(t), phân bố nhiệt q(x,t) trong vật
được điều khiển thông qua nhiệt độ của môi trường không
khí trong lò u(t), nhiệt độ này lại được điều khiển bởi công
suất w(t). Như vậy, thực chất sự phân bố nhiệt độ trong vật
q(x,t) sẽ phụ thuộc vào công suất w(t).

82 Mai Trung Thái, Nguyễn Thị Mai Hương
2.2. Phiếm hàm mục tiêu và điều kiện ràng buộc
Trong trường hợp này bài toán được đặt ra như sau: Hãy
xác định một hàm điều khiển tối ưu w(t) (0
t
T ) sao cho
làm cực tiểu phiếm hàm:
2
0
[ ( )] *( ) ( , ) minI w t q x q x T dx
(6)
Trong đó: q*(x) là phân bố nhiệt mong muốn, còn q(x,T)
là phân bố nhiệt độ trong vật tại thời điểm t = T, được hiểu
là cuối quá trình gia nhiệt đảm bảo sự đồng đều nhiệt độ
nhất trong toàn bộ vật nung.
Ràng buộc của hàm điều khiển là:
12
w(t)AA
(7)
với
12
;AA
tương ứng là giới hạn dưới và giới hạn trên
công suất cung cấp cho lò (W).
3. Lời giải của bài toán
Quá trình tìm lời giải tối ưu bao gồm hai bước:
- Bước 1: Tìm quan hệ giữa q(x,t) và tín hiệu điều khiển
w(t). Đây chính là việc giải phương trình truyền nhiệt
(quan hệ giữa u(t) và q(x,t)) với điều kiện biên loại 3 kết
hợp với phương trình vi phân thường có trễ (quan hệ giữa
w(t) và u(t)). Như vậy nếu chưa quan tâm tới bài toán tối
ưu thì ta có thể tính được trường nhiệt độ trong phôi khi
biết công suất cung cấp cho lò (biết vỏ tìm lõi).
- Bước 2: Tìm tín hiệu điều khiển tối ưu w*(t). Thay
q(x,t) tìm được ở bước 1 vào phiếm hàm (6), sau đó tìm ra
nghiệm tối ưu w*(t) bằng phương pháp số, khi đó ta sẽ
chuyển một phiếm hàm mục tiêu cần cực tiểu thành việc
cực tiểu hóa một hàm nhiều biến.
3.1. Tìm quan hệ giữa q(x,t) và tín hiệu điều khiển w(t)
Để giải phương trình (1) với các điều kiện đầu và điều
kiện biên (2), (3), (4) ta áp dụng phép biến đổi Laplace với
tham số thời gian t. Khi áp dụng phép biến đổi Laplace với
tham số thời gian t thì phương trình vi phân đạo hàm riêng
đã được đưa về phương trình vi phân thường đối với biến
x. Biến đổi Laplace phương trình (1), ta được:
2
2
( , ) ( , )
Q x s
a sQ x s
x
(8)
Trong đó:
( , ) ( , )Q x s L q x t
Sau khi biến đổi các điều kiện đầu và điều kiện biên (2),
(3), (4), ta được:
0
( , ) (0, ) ( )
x
Q x s Q s U s
x
(9)
( , ) 0
x
Q x s
x
(10)
Để giải bài toán này, [2] đã thay thế đối tượng có trễ (5)
thỏa mãn điều kiện / 10 bằng một khâu quán tính bậc
nhất theo xấp xỉ Taylor, [5] đã thay thế đối tượng có trễ
thỏa mãn điều kiện 6 ≤ / < 10 bằng khâu xấp xỉ Pade bậc
1, biến đổi Laplace phương trình (5) ta được:
▪ Theo Taylor, phương trình (5) trở thành:
1 ( ) W( ). s
s U s k s e
Hay
W(s)
( 1) ( ) 1
s U s k s
(11)
▪ Theo Pade 1, phương trình (5) trở thành:
1 ( ) W( ). s
s U s k s e
Hay
12
( 1) ( ) .W( ).12
s
s U s k s
s
(12)
Trong đó:
( ) ( ) ;U s L u t
W( ) w( )s L t
(13)
Nghiệm tổng quát của phương trình (8) là:
12
( , ) ( ) . ( ) .
ss
Q x s C s sh x C s ch x
aa
(14)
với C1(s) và C2(s) là các ẩn số cần tìm.
Từ các điều kiện biên (9), (10) ta tính được:
1
( ) .
()
. . . .
s
U s sh a
Cs s s s
sh ch
a a a
(15)
2
( ) .
()
. . . .
s
U s ch a
Cs s s s
sh ch
a a a
(16)
Thay (15), (16) vào (14) và từ (11), (12) sau khi biến
đổi ta được kết quả:
▪ Hàm Q(x,s) theo Taylor:
. ( )
( , ) W(s)
1 1 . .
s
k ch x a
Q x s s
ss
a
s s sh ch
aa
(17)
Đặt
. ( )
( , )
1 1 . .
s
k ch x a
G x s s
ss
a
s s sh ch
aa
(18)
Ta được Q(x,s) = G(x,s) .W(s) (19)
▪ Hàm Q(x,s) theo Pade 1:

ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 5(114).2017-Quyển 1 83
W( ). . 1 . ( )
2
( , )
1 . 1 . . . .
2
ss
s k ch x a
Q x s s
ss
a
s s sh ch
aa
(20)
Đặt
. 1 . ( )
2
( , )
1 . 1 . . . .
2
ss
k ch x a
G x s s
ss
a
s s sh ch
aa
(21)
Ta được: Q(x,s) = G(x,s) .W(s) (22)
Từ (19), (22), theo lý thuyết về tích chập ta có
q(x,t) = g(x,t)
w(t) (23)
Ta có thể viết :
0
( , ) ( , )w( )
t
q x t g x t d
(24)
Hoặc:
0
( , ) ( , )w( )
t
q x t g x t d
(25)
Trong đó:
1
( , ) ( , )g x t L G x s
(26)
Vì vậy, nếu biết được hàm g(x,t) ta sẽ tính được phân
bố nhiệt q(x,t) từ hàm điều khiển w(t). Muốn tìm được
q(x,t) trong biểu thức (25) ta cần tìm hàm (26). Dùng phép
biến đổi ngược hàm G(x,s), ta có kết quả:
▪ Hàm g(x,t) theo Taylor:
2
0
2
00
20
0 0 0
1
. ( ).
( , )
(1 )( )
kt
k k Cosk x
a
g x t k
k Cosk Sink
a a a
e
2
1
2
11
21
1 1 1
1()
(1 )( )
kt
kk Cosk x
a
k
k Cosk Sink
a a a
e
2
22
2
1
2 ( )
.
.
()
(1 )(1 ) .
i
t
i
ii
i
ii
i
k Cos x
ae
Sin Cos
a
a a a
(27)
với
01/k
;
11/k
▪ Hàm g(x,t) theo Pade 1:
2
0
22
0 0 0
20
0 0 0
. 2 . .
(2 ). . .
( , ) .
x
k k k Cosk kt
a
k
k Cosk Sink
a a a
g x t e
2
1
2
11
21
1 1 1
2. . .
.
.
(1 ).
kt
x
k k Cosk a
k
k Cosk Sink
a a a
e
2
2
2
22
. . 2 . .
.
()
(1 )(1 ) . .
2.
..
i
it
i
ii
k Cos
i
Sin Cos
ii a
a
i
x
ae
aa
(28)
với
01/k
;
12/k
Trong biểu thức (27), (28):
-
là hệ số truyền nhiệt từ không gian lò vào vật
(W/m2.độ);
-
là hệ số dẫn nhiệt của vật (W/m.độ);
-
là bề dày tấm (m);
- a là hệ số dẫn nhiệt độ (m2/s);
-
là thời gian trễ của lò (s);
-
là hằng số thời gian của lò (s);
- k là hệ số truyền tĩnh của lò
i
ia
(29)
•
i là nghiệm của phương trình siêu việt:
.
.
i i i
tg B
(30)
• Bi là hệ số BIO của vật liệu
3.2. Tìm tín hiệu điều khiển tối ưu w*(t) bằng phương
pháp số
Để tìm w*(t) ta phải cực tiểu hoá phiếm hàm (6), tức là:
2
0
[ ( )] [ *( ) ( , )] minI w t q x q x T dx
(31)
Hay:
2
00
[ ( )] *( ) ( , )w( ) min
T
I w t q x g x T d dx
(32)
Như [2], [5] dùng phương pháp tích phân số Simson để
số hóa các tích phân của phiếm hàm (32), trong đó:
Khoảng không gian là bề dày tấm từ 0 đến
ta chia
làm n phần bằng nhau (n là một số chẵn).
Khoảng thời gian từ 0 đến T ta cũng chia ra thành m
khoảng bằng nhau (m cũng là một số chẵn). Khi đó bài toán
tối ưu chính là tìm các w*j sao cho cực tiểu phiếm hàm:
84 Mai Trung Thái, Nguyễn Thị Mai Hương
2
*
[ ] ( )
00
nm
w F w i i ij j
ij
I c q a w
(33)
Ràng buộc của hàm điều khiển là:
12
wj
AA
với
( 0,1,..., )jm
(34)
Do đó bài toán được đặt ra là hãy tìm cực tiểu của hàm
(33) với n+1 biến wj tuân theo ràng buộc (34). Rõ ràng (33)
là hàm bậc hai của các biến wj và các ràng buộc (34) là
tuyến tính. Bài toán trở thành bài toán quy hoạch bậc hai
[2], [5]. Với bài toán này có thể tìm nghiệm đúng bằng
phương pháp số sau một số hữu hạn phép lặp.
Mặc dù nghiệm của bài toán quy hoạch bậc hai thu được
sau một số hữu hạn phép lặp nhưng thuật toán của nó phức
tạp hơn thuật toán của phương pháp đơn hình cho bài toán
quy hoạch tuyến tính. Vì thế, để đơn giản hoá cách giải ta
biểu diễn phiếm hàm mục tiêu dưới dạng:
0
[ ( )] *( ) ( , )I w t q x q x T dx
(35)
Áp dụng tương tự như trên, ta tính được giá trị tích phân
ở vế phải của (35) là:
*
00
[ (t)] L(w(t)) nm
i i ij j
ij
I w c q a w
(36)
Như vậy ta có thể thay thế việc tìm lời giải cho bài toán
(33) với ràng buộc (34) bằng việc cực tiểu hoá bài toán (36)
với ràng buộc (34). Dùng phương pháp đơn hình giải bài
toán (36), ta cũng sẽ nhận được phương án tối ưu của bài
toán sau một số hữu hạn phép lặp.
4. Các kết quả mô phỏng
Sau khi xây dựng các thuật toán và lập các chương trình
điều khiển, chúng tôi đã tiến hành chạy các chương trình
mô phỏng trên một mẫu Diatomite trong hai trường hợp để
kiểm chứng tính đúng đắn của các thuật toán.
4.1. Trường hợp 1: khi đối tượng có trễ thỏa mãn điều
kiện
/
10
4.1.1. Mô phỏng theo Taylor
• Các thông số vật lí của vật nung
= 60 (W/m2.độ);
= 0,2 (W/m.độ);
a = 3,6.10-7 (m2/s);
= 0,04 (m)
• Các thông số của lò nhiệt
= 1200 (s);
= 80 (s); k = 0,3
• Phân bố nhiệt độ yêu cầu: q*(x) = 400°C
• Thời gian nung cho phép: T = 5400 (s)
• Giới hạn dưới công suất: A1 = 1200 (W)
• Giới hạn trên công suất: A2 = 2800 (W)
• Giới hạn nhiệt độ lò:
0
( ) 600u t C
• Giới hạn bề mặt vật nung:
0
(0,t) 500qC
Hệ số BIO của vật nung như sau:
. 60.0,04 12
0.2
Bi
Đây là vật rất dầy vì có hệ số Bi > 0,5.
Ta có
1200 15 10
80
Để tính toán chế độ nung tối ưu, ta chọn số lớp không
gian là n = 6, số khoảng thời gian m = 36. Sau khi chạy
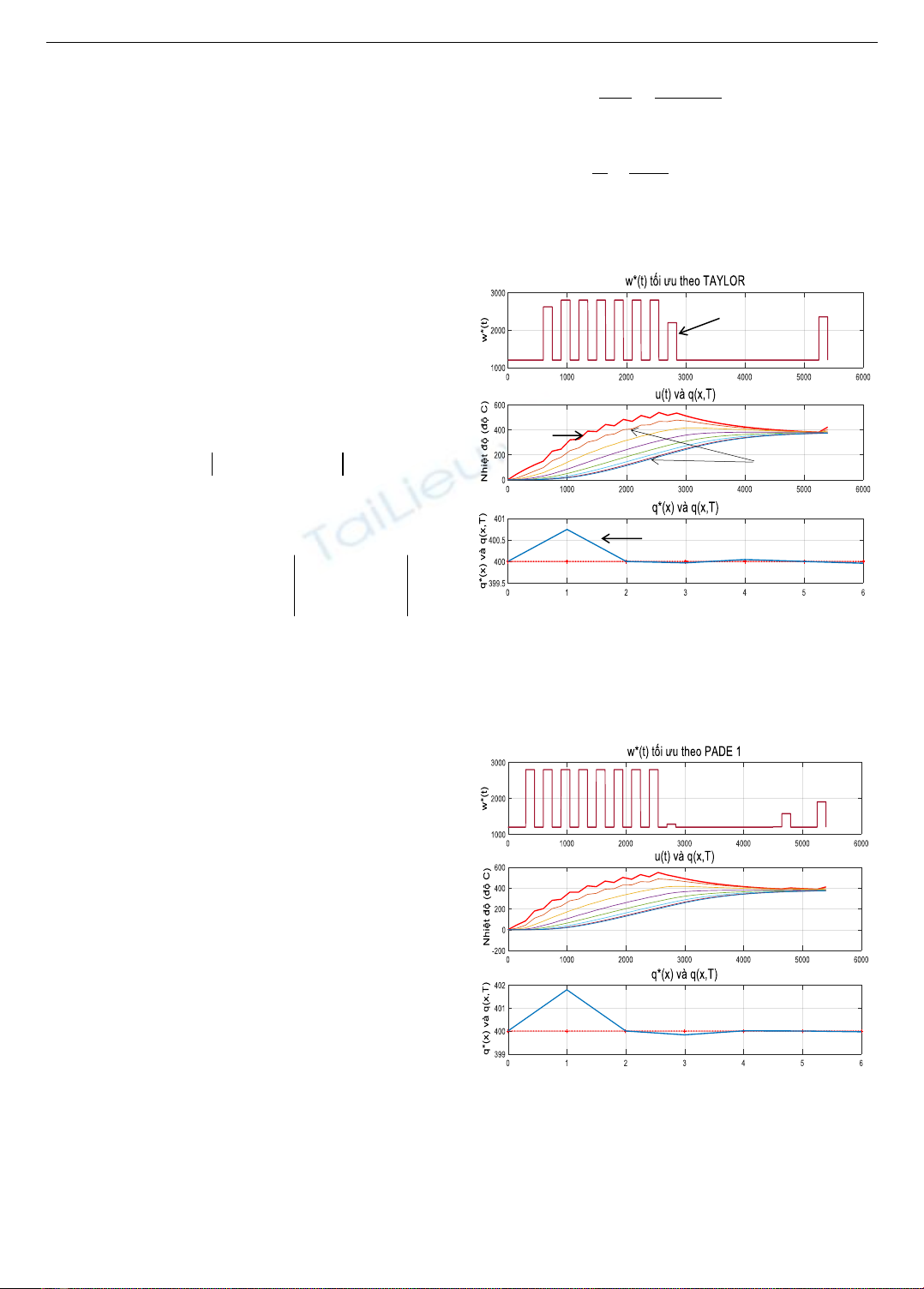
chương trình, ta được kết quả như Hình 1.
Hình 1. Chế độ nung tối ưu với mẫu Diatomite
(xấp xỉ theo Taylor, khi
= 80(s))
4.1.2. Mô phỏng theo Pade 1
Trong quá trình mô phỏng ta giữ nguyên tất cả các thông
số vật lý của đối tượng cũng như các thông số của lò nhiệt,
sau khi chạy chương trình ta được kết quả như hình 2
Hình 2. Chế độ nung tối ưu với mẫu Diatomite
( xấp xỉ theo Pade 1, khi
= 80(s))
4.2. Trường hợp 2: khi đối tượng có trễ thỏa mãn điều
kiện 6 ≤
/
< 10
Trong quá trình mô phỏng ta cũng giữ nguyên tất cả các
thông số như trường hợp 1, chỉ thay đổi thời gian trễ
,
trong trường hợp này cho
= 150 (s), khi đó ta có:
w*(t)
u(t)
q(x,T)
q(x,T)
ISSN 1859-1531 - TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ ĐẠI HỌC ĐÀ NẴNG, SỐ 5(114).2017-Quyển 1 85
1200
6 8 10
150
4.2.1. Mô phỏng theo Taylor
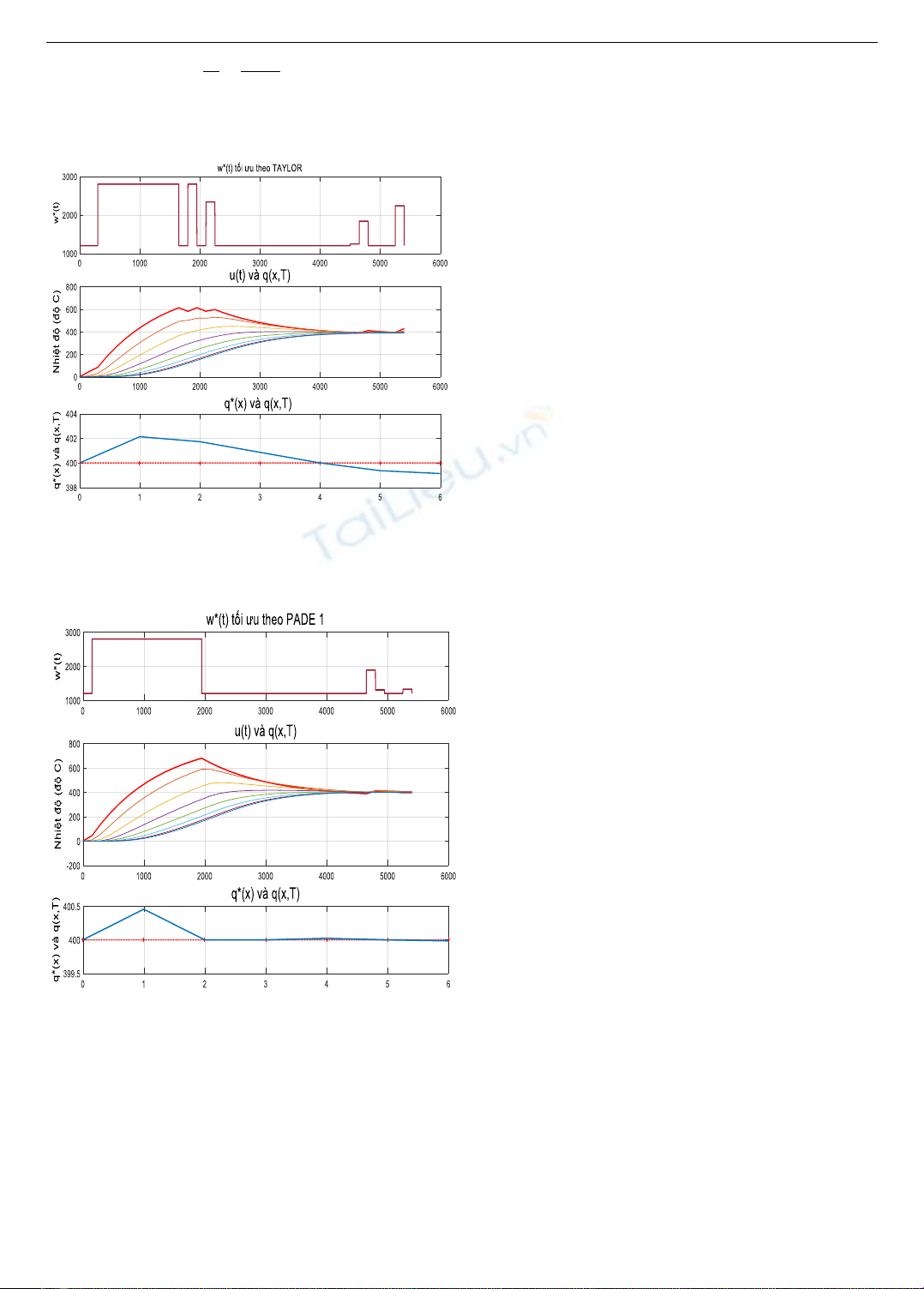
Sau khi chạy chương trình, ta được kết quả như Hình 3.
Hình 3: Chế độ nung tối ưu với mẫu Diatomite
(xấp xỉ theo Taylor, khi
= 150(s))
4.2.2. Mô phỏng theo Pade 1
Sau khi chạy chương trình ta được kết quả như Hình 4.
Hình 4. Chế độ nung tối ưu với mẫu Diatomite
( xấp xỉ theo Pade 1, khi
= 150(s))
5. So sánh giữa hai phương pháp
Hình 1 và Hình 2 chỉ ra rằng cả hai phương pháp tại
thời điểm t = T phân bố nhiệt độ tại các lớp q(x,T) đều xấp
xỉ 400°C, tuy nhiên khi xấp xỉ theo Taylor thì sai lệch lớn
nhất so với nhiệt độ đặt khoảng 0,7°C, còn theo Pade 1 thì
sai lệch lớn nhất khoảng 2°C, như vậy khi đối tượng có trễ
thỏa mãn điều kiện / 10 thì dùng phép xấp xỉ Taylor sẽ
có sai lệch nhỏ hơn so với phép xấp xỉ Pade 1 .
Hình 3 và Hình 4 cũng chỉ ra rằng tại thời điểm t = T
phân bố nhiệt độ tại các lớp q(x,T) đều xấp xỉ 400°C, nhưng
khi xấp xỉ theo Taylor thì sai lệch lớn nhất so với nhiệt độ
đặt khoảng 2°C, còn theo Pade 1 thì sai lệch lớn nhất
khoảng 0,5°C, như vậy khi đối tượng có trễ thỏa mãn điều
kiện 6 ≤ / <10 thì dùng phép xấp xỉ Pade 1 sẽ có sai lệch
nhỏ hơn so với phép xấp xỉ Taylor.
6. Kết luận
- Bài báo đã đưa ra hai mô hình thay thế cho một đối
tượng động học có trễ, đó là mô hình xấp xỉ Taylor và mô
hình xấp xỉ Pade bậc 1 để giải bài toán điều khiển tối ưu
cho một hệ có tham số phân bố, có trễ. Hệ này được ứng
dụng cho hệ thống truyền nhiệt một phía trong lò gia nhiệt
để điều khiển nhiệt độ cho phôi tấm theo tiêu chuẩn nung
chính xác nhất, tức là phải tìm một tín hiệu điều khiển tối
ưu sao cho sai số giữa phân bố trường nhiệt độ trong vật
nung với phân bố nhiệt độ yêu cầu là nhỏ nhất sau một
khoảng thời gian T cho trước.
- Các kết quả mô phỏng đã thể hiện tính đúng đắn của
các thuật toán, và hai phương pháp cũng chỉ ra rằng tùy
theo mối quan hệ giữa () và () thì ta nên dùng dạng xấp
xỉ nào là hợp lý nhất. Cụ thể, khi đối tượng có trễ mà có ()
và () thỏa mãn điều kiện / 10 thì dùng dạng xấp xỉ
Taylor sẽ có độ chính xác cao hơn, còn nếu đối tượng có
trễ thỏa mãn điều kiện 6 ≤ / < 10 thì phép xấp xỉ Pade
bậc 1 sẽ có độ chính xác cao hơn.
- Từ các kết luận như trên, các bài toán về nhận dạng
đối tượng điều khiển và thiết kế bộ điều khiển sẽ được hiệu
chỉnh sao cho phù hợp và mở ra khả năng áp dụng vào trong
thực tiễn.
TÀI LIỆU THAM KHẢO
[1] Errcan Celik, Mustafa Bayram, “On the numerical solution of
differential – algebraic equation by Pade series”, Applied
mathematics and computation, Vol. 137, 2003, pp.151-160.
[2] Cong Nguyen Huu, Nam Nguyen Hoai, “Optimal control for a
distributed parameter system with time delay based on the
numerical method”, 10th International Conference on Control,
Automation, Robotics and Vision, IEEE Conference, 2008,
pp.1612-1615.
[3] Y. Sakawa, “Solution of an optimal control problem in a distributed
parameter system”, Trans. IEEE, AC-9, 1964, pp. 420- 426.
[4] H.E. Lee, M.S., and Prof. D.W.C Shen, B.Sc., Ph.D., C.Eng.,
M.I.E.E, “Optimal control of a class of distributed-parameter
systems using gradient methods”, PROC. IEE, Vol.116, No.7, 1969,
pp. 1237 – 1244.
[5] Mai Trung.Thai, Nguyen Huu Cong, Nguyen Van Chi, Vu Dam
“Applying Pade Approximation Model in Optimal Control Problem
for a Distributed Parameter System With Time Delay”,
International Journal of Computing and Optimization, Vol. 4, No.1,
HIKARI Ltd, 2017, pp. 19-30.
(BBT nhận bài: 24/02/2017, hoàn tất thủ tục phản biện: 11/04/2017)























![Quyển ghi Xác suất và Thống kê [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251030/anh26012006/135x160/68811762164229.jpg)
