Tuyển tập Hội nghị Khoa học thường niên năm 2016. ISBN: 978-604-82-1980-2
172
BÓNG CỦA CÁC MẶT BẬC HAI ELLIPTIC
Nguyễn Thị Kim Hiền1, Nguyễn Hương Giang2
1Trường Đại học Thủy lợi, email: kimhien_hh@tlu.edu.vn
2 Trường Đại học Kiến trúc
1. GIỚI THIỆU CHUNG
Trong quá trình thiết lập bản vẽ nói chung
và bản vẽ kiến trúc nói riêng, để giúp cho bản
vẽ có tính biểu đạt cao, việc vẽ bóng đổ và
bóng bản thân là rất cần thiết, làm tăng thêm
hiệu quả về mặt thẩm mỹ.
Mặt bậc hai được ứng dụng khá phổ biến
trong thực tiễn. Việc vẽ bóng của các mặt bậc
hai tròn xoay đã được trình bày trong [1] và
[2] bằng các phương pháp khác nhau:
phương pháp mặt cắt tia sáng, phương pháp
tia ngược, phương pháp mặt tiếp xúc... Trong
phạm vi bài báo, xin trình bày cách vẽ bóng
của một số mặt bậc hai elliptic bằng phương
pháp afin phối cảnh.
2. PHƯƠNG PHÁP NGHIÊN CỨU
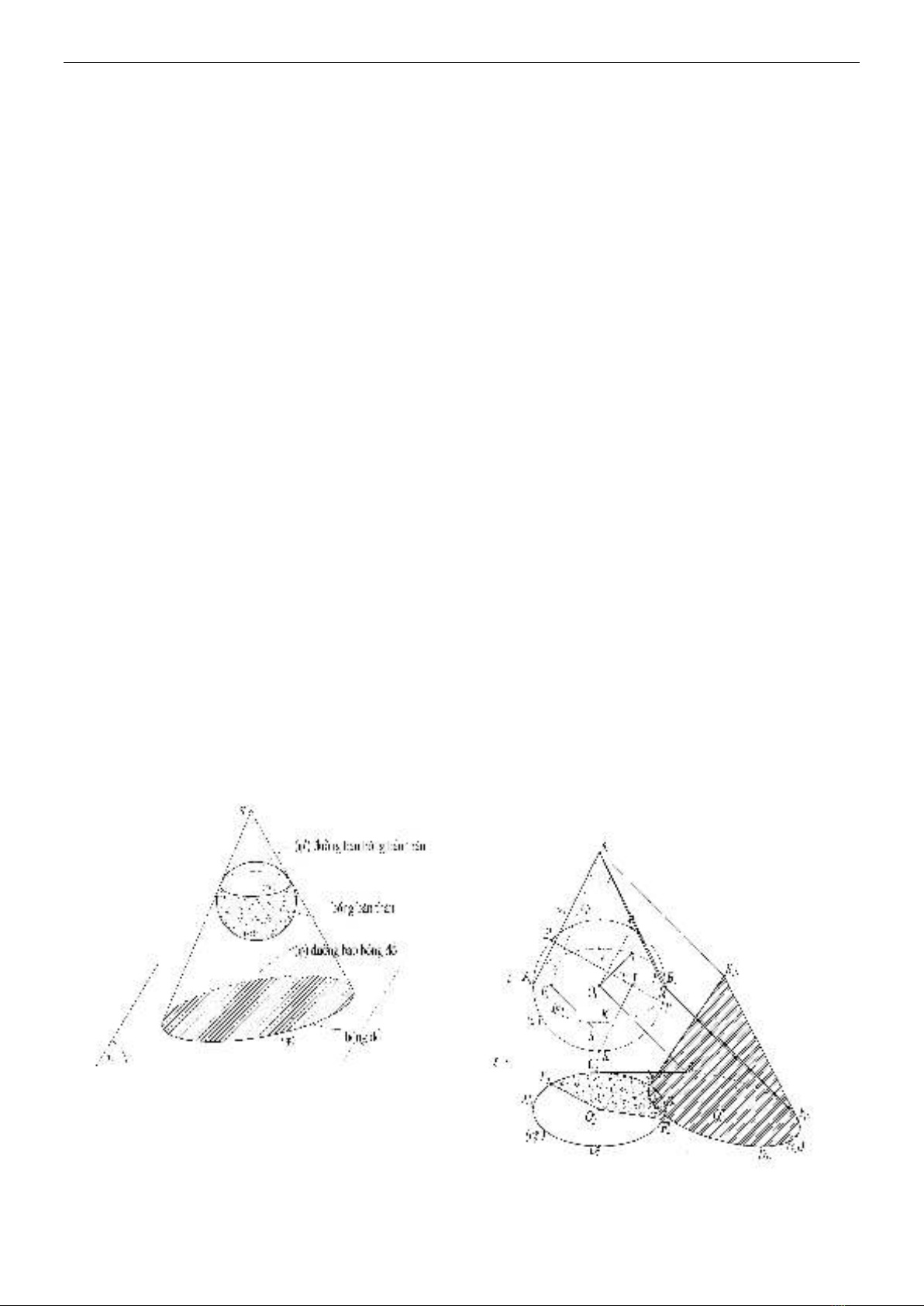
Hình 1: Nguyên tắc chung vẽ bóng
bản thân và bóng đổ
Nguyên tắc chung vẽ bóng bản thân và
bóng đổ lên một mặt phẳng bất kì (π) của một
mặt bậc hai (Ф) nào đó là vẽ chùm tia sáng
tiếp xúc với (Ф) từ nguồn sáng. Tập hợp tất
cả các điểm tiếp xúc giữa các tia sáng đó với
mặt bậc hai (Ф) sẽ cho ta đường bao quanh
bóng bản thân (φ’) và tập hợp tất cả giao điểm
của tia sáng đó với (Ф) sẽ cho ta đường bao
quanh bóng đổ trên () là đường bậc hai (φ).
Từ đây, ta suy ra cách vẽ bóng đổ được qui
về cách xác định giao tuyến giữa các mặt, hay
nói rõ hơn: "Đường bao quanh bóng đổ là bóng
đổ của đường bao quanh bóng bản thân". Có
nghĩa là có bóng bản thân ta có thể suy ra được
bóng đổ và ngược lại (xem hình 1).
Khi thực hiện phương pháp này cần xác
định được trục afin, hướng afin và một cặp
điểm tương ứng (xem [3] và [4]).
3. KẾT QUẢ NGHIÊN CỨU
3.1. Bóng của mặt nón elliptic
3.1.1. Bóng bản thân
Hình 2: Cách xác định bóng bản thân và
bóng đổ của mặt nón elliptic
Tuyển tập Hội nghị Khoa học thường niên năm 2016. ISBN: 978-604-82-1980-2
173
Dùng afin phối cảnh để biến đổi mặt nón
elliptic trục thẳng đứng
e
thành mặt nón
tròn xoay trục thẳng đứng
c
. Ta thấy
e
và
c
thuộc một tương ứng afin phối cảnh có
trục
1 1
t A B
, hướng afin
s
vuông góc với
t
,
cặp điểm tương ứng
'
K K
(xem hình 2).
3.1.2. Xác định bóng đổ
Trên hình vẽ
*
2
c
là hình chập lên mặt
phẳng hình chiếu bằng của đáy ellip
e
sao
cho
'
2
O
cách
một đoạn là
0
y
(
0
y
là độ xa
của điểm
O
). Bóng đổ trên hình chiếu đứng
của mặt nón bao gồm bóng đổ của hai đường
sinh bóng bản thân
,SE SF
và bóng đổ
1
b
c
của đáy nón.
Ta biết rằng,
*
2
c
và
1
b
c
thuộc một tương
ứng afin phối cảnh có trục là
t
, hướng afin là
l
//
t
. Ví dụ:
'
2
O
1b
O
,
b
F
, như trên
hình 2.
3.2. Bóng của mặt trụ elliptic
Mặt trụ elliptic là trường hợp đặc biệt của
mặt nón elliptic, khi đỉnh S ở ∞, khi đó các
đường sinh song song nhau.
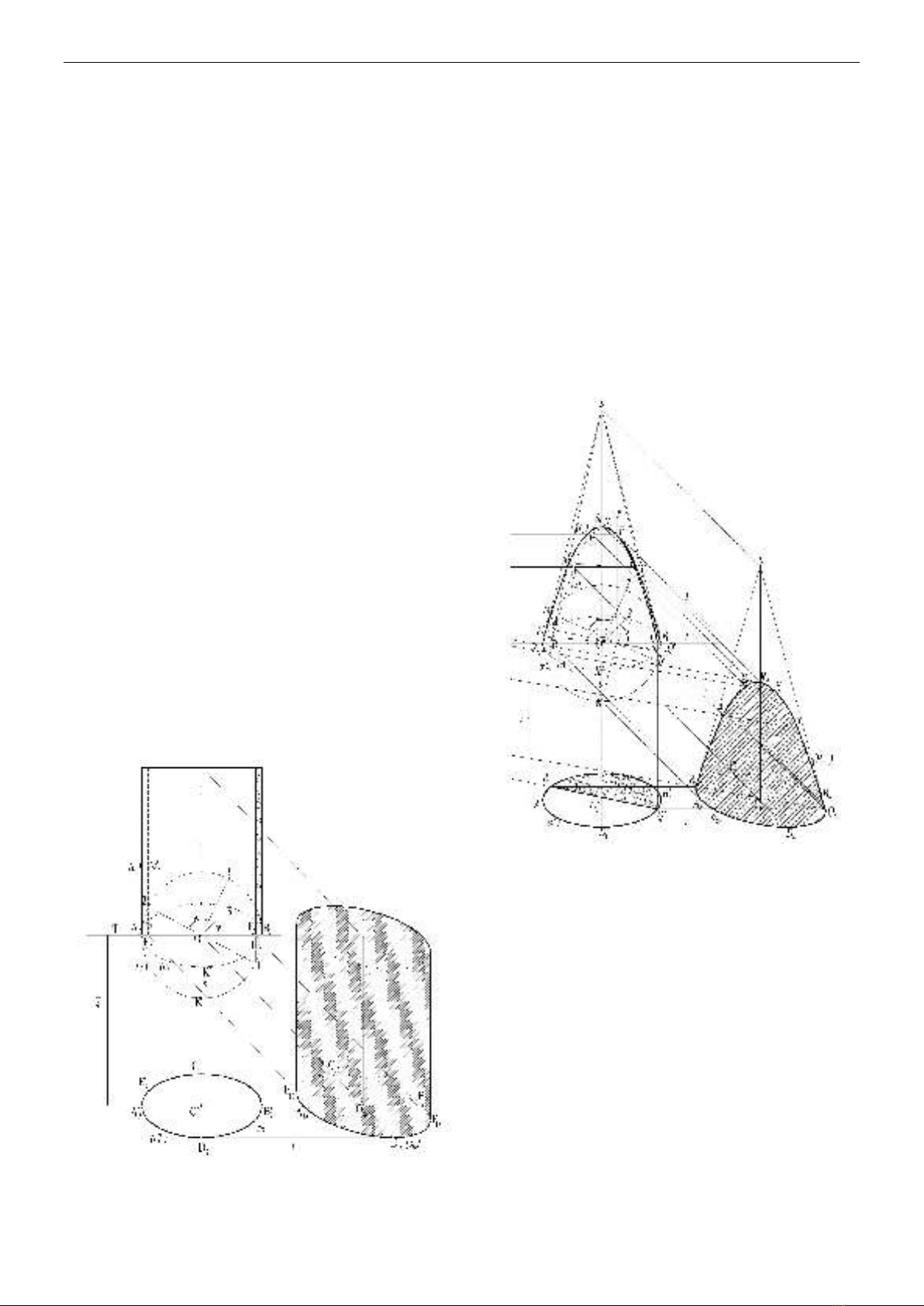
Hình 3: Cách xác định bóng bản thân và
bóng đổ của mặt trụ elliptic
3.3. Bóng của mặt Paraboloid elliptic
3.3.1. Xác định bóng bản thân
Gọi mặt nón đỉnh T là mặt nón ngoại tiếp
mặt Paraboloid elliptic.
Dùng afin phối cảnh để biến đổi mặt
Paraboloid elliptic trục thẳng đứng
e
thành
mặt Paraboloid tròn xoay trục thẳng đứng
c
. Dễ dàng thấy
e
và
c
thuộc một tương
ứng afin phối cảnh trục
1 1
t A B
, hướng afin
s
vuông góc với
t
, cặp điểm tương ứng
'
K K
(xem hình 4).
Hình 4: Cách xác định bóng bản thân và
bóng đổ của mặt Paraboloid elliptic
3.3.2. Xác định bóng đổ
Giữa
*
2
c
và
1
b
c
nằm trong một tương
ứng afin phối cảnh trục là
t
, hướng afin
'
l
//
t
. Ví dụ :
'
2
O
1b
O
.
1
b
c
nhận
1 1b b
A B
và
1 1b b
C D
làm hai đường kính liên hiệp (hình
chiếu song song của hai đường kính vuông
góc AB và CD).
'
1
c
và
1
b
p
thuộc một
tương ứng afin phối cảnh có trục là
" '
1 1 1
R
b
t c p V
(vết đứng của
'
1
c
),
hướng afin
l
nghiêng 450 so với
x
, tam giác
hướng afin là
1
'Q Q I
(xem hình 4).
Tuyển tập Hội nghị Khoa học thường niên năm 2016. ISBN: 978-604-82-1980-2
174
3.4. Bóng của mặt Hyperboloid elliptic
1 tầng
3.4.1. Xác định bóng bản thân
Gọi
*
2
c
và
*
2
e
lần lượt là hình chập của
đáy ellip và nón tiệm cận của mặt
Hyperboloid elliptic, sao cho
'
2
O
cách
x
một
đoạn bằng
0
y
(
0
y
là độ xa của tâm ellip đáy).
Dùng afin phối cảnh để biến đổi mặt
Hyperboloid elliptic trục thẳng đứng thành
mặt Hyperboloid tròn xoay trục thẳng đứng.
*
2
c
và
c
thuộc một tương ứng afin phối
cảnh trục
' '
2 2
t C D
, hướng afin
s
vuông góc
với
t
, cặp điểm tương ứng
'
2
Q Q
.
*
2
e
và
e
thuộc một tương ứng afin phối cảnh trục
' '
2 2
t C D
, hướng afin
s
vu«ng gãc víi
t
, cÆp
®iÓm t¬ng øng
'
K K
.
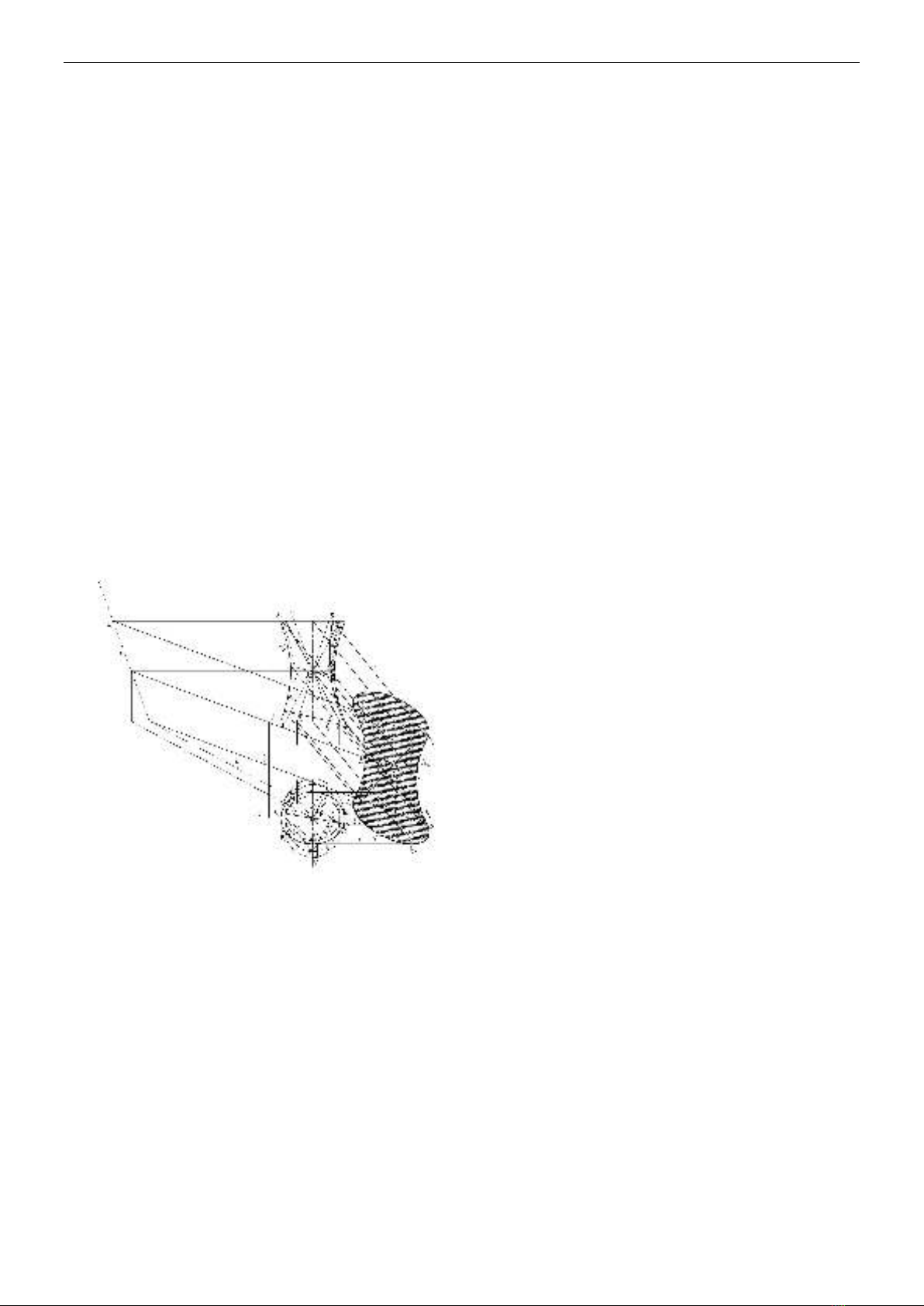
Hình 5: Cách xác định bóng bản thân và
bóng đổ của mặt Hyperboloid elliptic 1 tầng
3.4.2. Xác định bóng đổ
Gọi
'
1
b
c
và
1
b
h
lần lượt là bóng đổ trên
hình chiếu đứng của đáy elliptic và
Hyperboloid. Giữa
*
2
c
và
1
b
c
nằm trong
một tương ứng afin phối cảnh trục là
x
,
hướng afin
'
l
//
d
.
1
b
c
nhận
1 1b b
A B
và
1 1b b
P Q
làm hai đường kính liên hiệp (hình chiếu
song song của hai đường kính vuông góc AB
và PQ).
1
c
và
1
b
h
thuộc một tương ứng
afin phối cảnh có trục là
" '
1 1 1
R
b
t c h V
(vết đứng của
'
1
c
) hướng
afin
l
nghiêng 450 so với
x
, tam giác hướng
afin là
'
1 1
l O l
.
Ví dụ:
1 1
1 1 b
,
1 1
2 2 b
,
1 1b
O O
. Mọi
điểm trên
'
1
c
cho ta điểm tương ứng trên
1
b
h
. Bóng đổ trên hình chiếu đứng
1
b
h
của
mặt Hyperboloid elliptic nhận bóng đổ của
đường bao bóng bản thân nón tiệm cận trên
hình chiếu đứng làm tiệm cận.
4. KẾT LUẬN
Phương pháp afin phối cảnh cho ta kết quả
vẽ bóng chính xác của bất kì điểm nào thuộc
mặt bậc hai cần vẽ, trong khi các phương
pháp khác còn bị hạn chế. Trong khi một số
tài liệu chỉ nêu được bóng của những mặt bậc
hai tròn xoay, bài báo này đã nêu được cách
vẽ bóng bản thân và bóng đổ cho các mặt bậc
hai elliptic.
5. TÀI LIỆU THAM KHẢO
[1] Nguyễn Đình Điện, Đỗ Mạnh Môn. Hình
học hoạ hình Tập 1,2. NXB GD.
[2] Hoàng Văn Thân, Dương Tiến Thọ, Đỗ
Mạnh Môn, Nguyễn Văn Tuấn. Hình học
hoạ hình Vẽ bóng trên bản vẽ kiến trúc.
NXBXD.
[3] Nguyễn Cảnh Toàn. Hình học xạ ảnh.
NXBGD.
[4] Hoàng Văn Thân. Phương pháp xạ ảnh giải
một số bài toán với mặt bậc hai.