Trang 1
V n đ 1: DAO Đ NG C H Cấ ề Ộ Ơ Ọ
I. CON L C LÒ XOẮ
1. Ph ng trình dao đ ngươ ộ :
cos( )x A t
ω ϕ
= +
2. Ph ng trình v n t cươ ậ ố :
'; sin( ) cos( )
2
dx
v x v A t A t
dt
π
ω ω ϕ ω ω ϕ
= = = − + = + +
3. Ph ng trình gia t cươ ố :
22 2
2
'; ''; cos( );
dv d x
a v a x a A t a x
dt dt
ω ω ϕ ω
= = = = = − + = −
Hay
2
cos( )a A t
ω ω ϕ π
= +
4. T n s góc, chu kì, t n s và pha dao đ ng, pha ban đ uầ ố ầ ố ộ ầ :
a. T n s góc: ầ ố
2
2 ( / ); k g
f rad s
T m l
π
ω π ω
= = = = ∆
;
( )
mg
l m
k
∆ =
b. T n s : ầ ố
1 1
( ); 2 2
N k
f Hz f
T t m
ω
π π
= = = =
c. Chu kì:
1 2
( ); 2
t m
T s T
f N k
ππ
ω
= = = =
d. Pha dao đ ng: ộ
e. Pha ban đ u: ầ
ϕ
Chú ý: Tìm
ϕ
, ta d a vào h ph ng trình ự ệ ươ
0
0
cos
sin
x A
v A
ϕ
ω ϕ
=
= −
lúc
0
0t=
M T S TR NG H P TH NG G PỘ Ố ƯỜ Ợ ƯỜ Ặ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí cân b ng ậ ị ằ
0
0x=
theo chi u d ng ề ươ
0
0v>
: Pha
ban đ u ầ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí cân b ng ậ ị ằ
0
0x=
theo chi u âm ề
0
0v<
: Pha ban
đ u ầ
2
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua biên d ngậ ươ
0
x A=
: Pha ban đ u ầ
0
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua biên âmậ
0
x A= −
: Pha ban đ u ầ
ϕ π
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x=
theo chi u d ng ề ươ
0
0v>
: Pha ban đ uầ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x= −
theo chi u d ng ề ươ
0
0v>
: Pha ban đ uầ
π
ϕ
= − 2
3
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x=
theo chi u âm ề
0
0v<
: Pha ban đ uầ
3
π
ϕ
=
Ngày mai b t đ u t ngày hôm nayắầừ
Trang 2
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x= −
theo chi u âm ề
0
0v<
: Pha ban đ uầ
2
3
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x=
theo chi u d ng ề ươ
0
0v>
: Pha ban
đ u ầ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x= −
theo chi u d ng ề ươ
0
0v>
: Pha ban
đ u ầ
π
ϕ
= − 3
4
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x=
theo chi u âm ề
0
0v<
: Pha ban đ uầ
4
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x= −
theo chi u âm ề
0
0v<
: Pha ban đ uầ
3
4
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x=
theo chi u d ng ề ươ
0
0v>
: Pha ban
đ u ầ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x= −
theo chi u d ng ề ươ
0
0v>
: Pha ban
đ u ầ
π
ϕ
= − 5
6
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x=
theo chi u âm ề
0
0v<
: Pha ban đ uầ
6
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x= −
theo chi u âm ề
0
0v<
: Pha ban đ uầ
5
6
π
ϕ
=
♦
cos sin( )
2
π
α α
= +
;
sin cos( )
2
π
α α
= −
Giaù trò caùc haøm soá löôïng giaùc cuûa caùc cung (goùc ) ñaëc bieät (ta neân söû duïng
ñöôøng troøn löôïng giaùc ñeå ghi nhôù caùc giaù trò ñaëc bieät)
Ngày mai b t đ u t ngày hôm nayắầừ
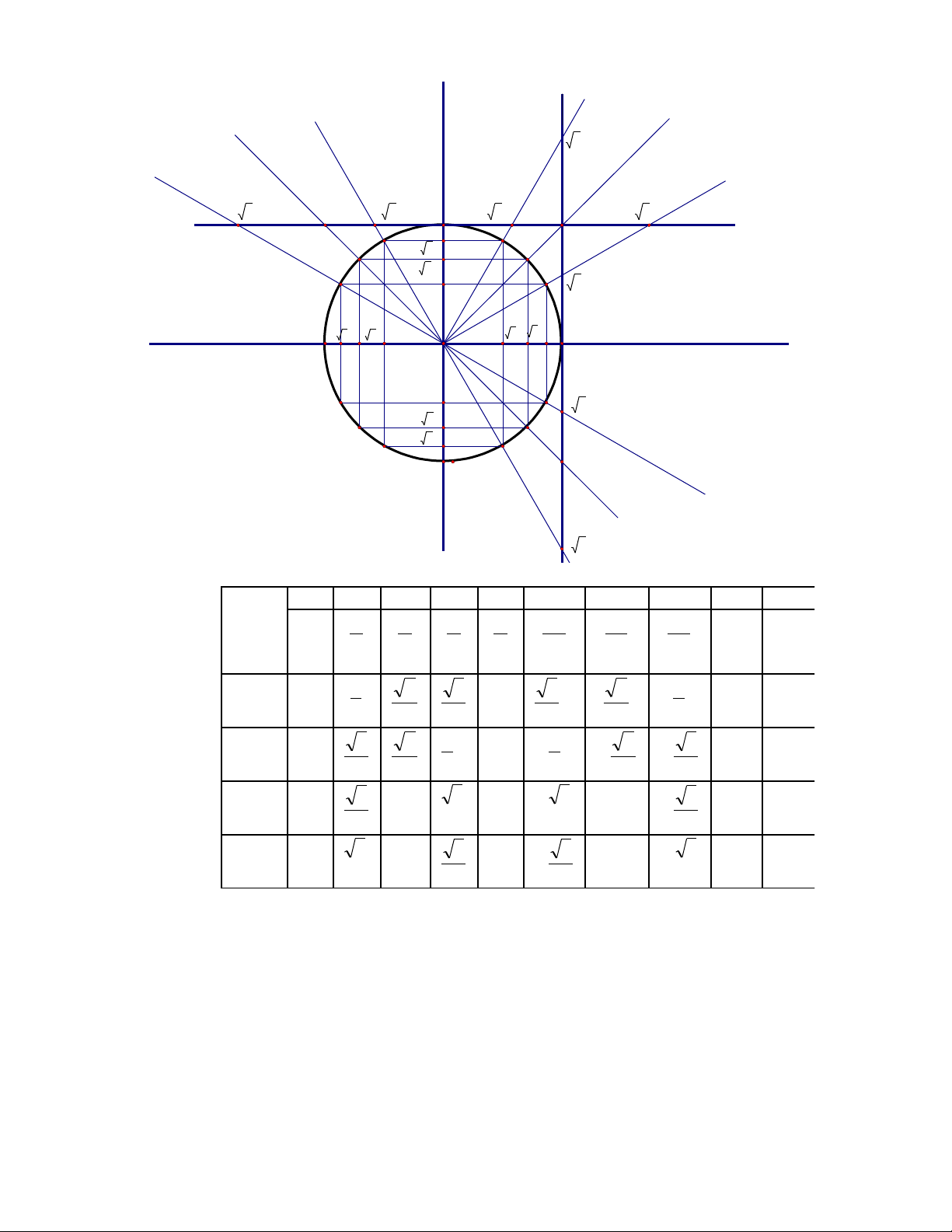
Trang 3
-
3
-1
-
3
/3
(Ñieåm goác)
t
t'
y
y'
x
x'
u
u'
-
3
-1
-
3
/3
1
1
-1
-1
-
π
/2
π
5
π
/6
3
π
/4
2
π
/3
-
π
/6
-
π
/4
-
π
/3
-1/2
-
2
/2
-
3
/2
-1/2
-
2
/2
-
3
/2
3
/2
2
/2
1/2
3
/2
2
/2
1/2
A
π
/3
π
/4
π
/6
3
/3
3
B
π
/2
3
/3
1
3
O
Ngày mai b t đ u t ngày hôm nayắầừ
Goù
c
Hslg
0030
045
0 60
090
0120
0135
0150
0180
0360
0
0
6
π
4
π
3
π
2
π
3
2
π
4
3
π
6
5
π
π
π
2
sin
α
0
2
1
2
2
2
3
1
2
3
2
2
2
1
0 0
cos
α
1
2
3
2
2
2
1
0
2
1
−
2
2
−
2
3
−
-1 1
tg
α
0
3
3
1
3
kxñ
3−
-1
3
3
−
0 0
cotg
α
kxñ
3
1
3
3
0
3
3
−
-1
3−
kxñ kxñ
Trang 4
5. Ph ng trình đ c l p v i th i gian:ươ ộ ậ ớ ờ
ω
= +
2
2 2
2
v
A x
;
ω ω
= +
2 2
2
4 2
a v
A
Chú ý:
2
: Va�t qua v� tr� ca�n ba�ng
: Va�t �� bie�n
MM
M
M
v A a
v
a A
ωω
ω
=
=�
=
6. L c đàn h i, l c h i ph cự ồ ự ồ ụ :
a. L c đàn h i: ự ồ
( )
( ) ( ) ne�u
0 ne�u l A
hM�
h hm� �
hm�
F k l A
F k l x F k l A l A
F
= ∆ +
= ∆ + = ∆ − ∆ >�= ∆
b. L c h i ph c: ự ồ ụ
0
hpM
hp
hpm
F kA
F kx F
=
= =
hay
2
0
hpM
hp
hpm
F m A
F ma F
ω
=
= =
l c h i ph c luôn h ngự ồ ụ ướ
vào v trí cân b ng. ị ằ
Chú ý: Khi h dao đ ng theo ph ng n m ngang thì l c đàn h i và l c h i ph c là nh nhau ệ ộ ươ ằ ự ồ ự ồ ụ ư
h hp�
F F=
.
7. Th i gian, quãng đ ng, t c đ trung bìnhờ ườ ố ộ
a. Th i gian: Gi i ph ng trình ờ ả ươ
cos( )
i i
x A t
ω ϕ
= +
tìm
i
t
Chú ý:
G i O là trung đi m c a qu đ o CD và M là trung đi m c a OD; th i gian đi t O đ n Mọ ể ủ ỹ ạ ể ủ ờ ừ ế
là
12
OM
T
t=
, th i gian đi t M đ n D là ờ ừ ế
.
T v trí cân b ng ừ ị ằ
0x
=
ra v trí ị
2
2
x A=
m t kho ng th i gian ấ ả ờ
8
T
t=
.
T v trí cân b ng ừ ị ằ
0x
=
ra v trí ị
3
2
x A=
m t kho ng th i gian ấ ả ờ
6
T
t=
.
Chuy n đ ng t O đ n D là chuy n đ ng ch m d n (ể ộ ừ ế ể ộ ậ ầ
0; av a v<
r r
), chuy n đ ng t Dể ộ ừ
đ n O là chuy n đ ng nhanh d n (ế ể ộ ầ
0; av a v>
r r
)
V n t c c c đ i khi qua v trí cân b ng (li đ b ng không), b ng không khi biên (li đậ ố ự ạ ị ằ ộ ằ ằ ở ộ
c c đ i).ự ạ
b. Quãng đ ng:ườ
Ne�u th�
4
Ne�u th� 2
2
Ne�u th� 4
T
t s A
T
t s A
t T s A
= =
= =
= =
suy ra
Ne�u th� 4
Ne�u th� 4
4
Ne�u th� 4 2
2
t nT s n A
T
t nT s n A A
T
t nT s n A A
= =
= + = +
= + = +
Chú ý:
Ngày mai b t đ u t ngày hôm nayắầừ
Trang 5
2 2
2 ne�u va�t �i t��
2 2
ne�u va�t �i t��
4
M
s A x A x A
T
ts A x O x A
= = =
= = = =
m ﾀ
( )
2 2
2 2 ne�u va�t �i t��
2 2
2 2
ne�u va�t �i t�� 0
2 2
82 2
1 ne�u va�t �i t��
2 2
m
M
m
s A x A x A x A
s A x x A
T
t
s A x A x A
= − = = =
= = =
= � �
= − = =
� �
� �
� �
ﾀ ﾀ
( )
3 3
ne�u va�t �i t�� 0
2 2
ne�u va�t �i t��
62 2
3 3
2 3 ne�u va�t �i t��
2 2
M
m
s A x x A
TA A
ts x x A
s A x A x A x A
= = =
= = = =
= − = = = ﾀ ﾀ
ne�u va�t �i t�� 0
2 2
3 3
12 1 ne�u va�t �i t��
2 2
M
m
A A
s x x
T
t
s A x A x A
= = =
=
� �
= − = =
� �
� �
� �
c. T c đ trung bình: ố ộ
tb
s
vt
=
8. Năng l ng trong dao đ ng đi u hòaượ ộ ề :
t�
E E E= +
a. Đ ng năng: ộ
2 2 2 2 2
1 1 sin ( ) sin ( )
2 2
￱
E mv m A t E t
ω ω ϕ ω ϕ
= = + = +
b. Th năng: ế
2 2 2 2 2
1 1 cos ( ) cos ( );
2 2
t
E kx kA t E t k m
ω ϕ ω ϕ ω
= = + = + =
Chú ý:
2 2 2
2 2 2
2
1 1
2 2
1 1 : Va�t qua v� tr� ca�n ba�ng
2 2
1: Va�t �� bie�n
2
M M�
tM
E m A kA
E mv m A
E kA
ω
ω
= =
= =
=
Th năng và đ ng năng c a v t bi n thiên tu n hoàn v i ế ộ ủ ậ ế ấ ớ
' 2
'2
' 2
f f
T
T
ω ω
=
=
=
c a dao đ ng.ủ ộ
Trong m t chu kì, ch t đi m qua v trí ộ ấ ể ị
=
0
x x
là 4 l n, nên ầ
( )
π
ω ϕ α
+ = + 2
t k
9. Chu kì c a h lò xo ghépủ ệ :
a. Ghép n i ti p: ố ế
2 2
1 2
1 2
1 1 1 T T T
k k k
= + = +�
Ngày mai b t đ u t ngày hôm nayắầừ
12
T
3
2A+
3
2A−
2
2A+
2
2A−
1
2A+
1
2A−
A+
A−
x
6
T
6
T
6
T