Gv. Cao Haøo Thi
CHÖÔNG 4
LAÁY MAÃU VAØ PHAÂN PHOÁI MAÃU
(Sampling and Sampling Distribution)
4.1. LAÁY MAÃU TÖØ TAÄP HÔÏP CHÍNH (Sampling from a Population)
4.1.1. Taäp hôïp chính (Population)
Taäp hôïp chính laø taäp hôïp taát caû caùc ñoái töông maø ta quan taâm nghieân cöùu trong moät vaán
ñeà naøo ñoù. Soá phaàn töû cuûa taäp hôïp chính ñöôïc kyù hieäu laø N.
• Neáu N laø soá höõu haïn ta coù taäp hôïp chính höõu haïn (finite population)
• Neáu N laø soá voâ haïn ta coù taäp hôïp chính voâ haïn (infinite population)
4.1.2. Maãu (Sample)
Maãu laø taäp hôïp con cuûa taäp hôïp chính. Soá phaàn töû cuûa maãu ñaõ kyù hieäu laø n vaø ñöôïc goïi
laø côõ maãu.
4.1.3. Laáy maãu ngaãu nhieân ñôn giaûn (Simple Random Sampling)
Ñoù laø caùch choïn n phaàn töû töø taäp hôïp chính goàm N phaàn töû sao moãi toå hôïp trong n
N
C toå
hôïp ñeàu coù cuøng khaû naêng ñöôïc choïn nhö nhau. Keát quaû cuûa vieäc choïn naøy cho ta caùc
maãu ngaãu nhieân (random sample).
Vieäc laáy maãu ngaãu nhieân coù theå tieán haønh theo caùch laáy maãu khoâng hoaøn traû laïi
(sampling without replacement) hay theo caùch laáy maãu coù hoaøn traû laïi (sampling with
replacement).
4.1.4. Phaân phoái maãu (Sampling Distribution)
Caùc maãu ñeàu coù caùc ñaëc tröng thoáng keâ cuûa maãu nhö soá trung bình X, phuông sai 2
x
S.
Phaân phoái xaùc suaát cuûa caùc ñaëc tröng thoáng keâ cuûa maãu ñöôïc goïi laø phaân phoái maãu.
Trong chöông naøy ta khaûo saùt phaân phoái maãu cuûa X, 2
x
S.
Suy dieãn thoáng keâ (Statistic Inference)
Döïa vaøo caùc ñaëc tröng thoáng keâ cuûa maãu ta coù theå suy roäng ra cho caùc ñaëc tröng thoáng
keâ cuûa taäp hôïp chính.
4.2. PHAÂN PHOÁI MAÃU CUÛA SOÁ TRUNG BÌNH CUÛA MAÃU X (Sampling Distribution
of the Sample Mean)
Phaân phoái maãu cuûa soá trung bình cuûa maãu laø phaân phoái xaùc suaát cuûa ñaïi löôïng X
4.2.1. Kyø voïng cuûa soá trung bình maãu E (X)
Giaû söû taäp hôïp chính coù N phaân töû, coù trung bình laø µx vaø phöông sai laø 2
x
σ. Ta coù:
Gv. Cao Haøo Thi
2
N
X
N
ii
x
∑
=µ =1
N
)X(
N
ii
x
∑µ−
=σ =1
2
2
Goïi X1, X2 ... Xn laø maãu ngaãu nhieân coù côõ maãu laø n, ñöôïc choïn töø taäp hôïp chính. Soá
trung bình cuûa maãu laø :
∑
=i
X
n
X1
• Kyø voïng cuûa soá trung bình maãu cuûa soá trung bình maãu E ( X) laø giaù trò trung bình
cuûa taäp hôïp chính µx. Noùi caùch khaùc, phaân phoái maãu cuûa X coù soá trung bình laø µx.
E( X ) = µx
Thí duï:
Giaû söû taäp hôïp chính goàm 5 hoïc sinh coù soá tuoåi laø 2, 4, 6, 8 vaø 10. Trong tröôøng hôïp naøy
soá trung bình cuûa taäp hôïp chính seõ laø
µx = 1/5(2+4+6+8+10) = 6
Giaû söû laáy maãu ngaãu nhieân khoâng hoaøn laïi vôùi côõ maãu laø 2. Ta seõ coù 2
5
C = 10 maãu khaùc
nhau (vôùi côõ maãu laø 2). Vaø moãi maãu seõ coù soá trung bình cuûa maãu X nhö sau :
Sample 2,4 2,6 2,8 2,10 4,6 4,8 4,10 6,8 6,10 8,10
X 3 4 5 6 5 6 7 7 8 9
Phaân phoái maãu cuûa soá trung bình X laø :
(Phaân phoái xaùc suaát cuûa ñaëc tröng thoáng keâ cuûa maãu X
Sample 3 4 5 6 7 8 9 10
X 0.1 0.1 0.2 0.2 0.2 0.1 0.1 0.1
Kyø voïng cuûa X
E( X ) = ΣX * p( X)
= 3 * 0.1 + 4 * 0.1 + 5 * 0.2 + 6 * 0.2 + 7 * 0.2 + 8 * 0.1 + 9 * 0.1
E( X) = 6 = µx
4.2.2. Phöông sai cuûa soá trung bình maãu ( 2
X
σ)
Tröôøng hôïp taäp hôïp chính voâ haïn (Infinite Polulation)
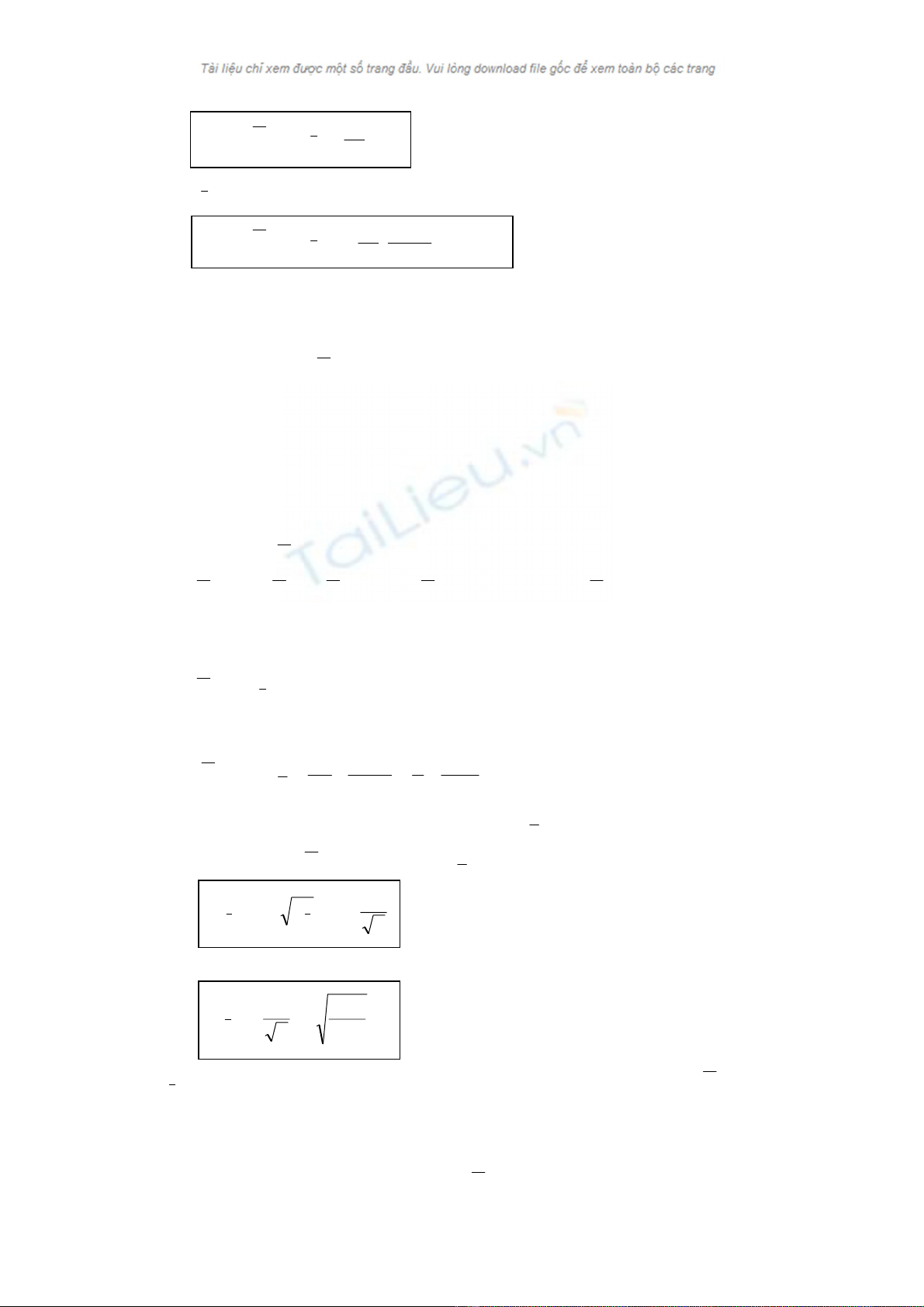
Phöông sai cuûa soá trung bình maãu X ñöôïc kyù hieäu laø σ2
x
Gv. Cao Haøo Thi
3
Var (X) = σ2
x = nx
σ2 Ñuùng khi n < N
Vôùi σ2
x laø phöông sai cuûa taäp hôïp chính, n laø côõ maãu.
Var (X) = σ2
x = )( 1N
nN
n
2
x
−
−
σ
Tröôøng hôïp taäp hôïp chính höõu haïn (Finite Population)
Thí duï:
Tính phöông sai cuûa X trong thí duï treân
Phöông sai cuûa taäp hôïp chính
σ2
x = E[(Xi - µx)² = Σ(xi - µx)² * P(Xi) µx = 6; P(Xi) = 1/5
= 1/5[(2-6)² + (4 - 6)² + (6 -6 )² + (8-6)² + (10 - 6)²]
σ2
x = 8
Phöông sai cuûa X tính töø ñònh nghóa
Var (X ) = E [( X - E( X))
2] = E [(X- 6)
2] vì E ( X) = µx = 6
= [(3-6)2 * 0.1 + (4-6)2 * 0.1 + (5-6)2 * 0.2 + (6-6)2 * 0.2 + (7-6)2 * 0.2
+( 8-6)2 * 0.1 + (9-6)2 * 0.1]
Var (X) = σ2
x = 3
Neáu aùp duïng coâng thöùc :
Var (X ) = 3
15
25
2
8
1N
nN
n
2
x
2
X=
−
−
=
−
−
σ
=
σ**
4.2.3. Ñoä leäch chuaån cuûa soá trung bình maãu ( X
σ
)
Ñoä leäch chuaån cuûa X ñöôïc kyù hieäu ( X
σ
)
σσ
σ
xx
x
n
==
2 Ñoái vôùi taäp hôïp chính voâ haïn
hay
1N
nN
n
x
x−
−
σ
=σ * Ñoái vôùi taäp hôïp chính höõu haïn
x
σñöôïc xem nhö sai soá chuaån (Standard Error) cuûa soá trung bình maãu X.
4.2.4. Laáy maãu töø taäp hôïp chính tuaân theo phaân phoái chuaån (Sampling From Normal
Population)
Luaät phaân phoái cuûa soá trung bình maãu X
Gv. Cao Haøo Thi
4
Neáu taäp hôïp chính cuûa bieán X tuaân theo phaân phoái chuaån vôùi soá trung bình laø µx vaø
phöông sai σx thì soá trung bình maãu X seõ tuaân theo phaân phoái chuaån vôùi soá trung trình
laø µx vaø phöông sai laø n
2
x/σ.
X ~ X N 2
xX ==>σµ ),( ~ Nn
X
X
(, )µσ2
4.2.5. Chuaån hoùa soá trung bình maãu X
Ñaët : ZXX
X
=−µ
σ
Neáu X coù soá trung bình laø µx vaø phöông sai laø σ2
X thì Z coù soá trung bình laø 0 vaø
phöông sai laø 1.
Neáu
(
)
(
)
10
2,N~Z ,N~X X
x==>
σ
µ
4.2.6. Ñònh lyù giôùi haïn trung taâm (Central Limit Theorem)
Khi n lôùn thì
n
X
Z
X
X
σ
µ−
= seõ gaàn ñuùng coù phaân phoái chuaån chuaån hoùa hay X coù phaân
phoái chuaån vôùi soá trung bình hoaù laø µx phöông sai n
x
2
σ
Khi n lôùn ==> Z ~ N(0, 1) hay XN n
X
X
~,µσ2
Thí duï :
Chieàu daøi cuûa caùc caây thöôùc keû trong daây chuyeàn saûn xuaát thöôùc tuaân theo phaân phoái
chuaån vôùi µ = 30cm. Ñoä leäch chuaån xung quanh soá trung trung bình laø δ = 0.1cm. Nhaân
vieân thanh tra laáy maãu vôùi côõ maã n = 4 vaø nhaän thaáy soá trung bình cuûa maãu laø X =
29875cm.
Tìm xaùc suaát ñeå soá trung bình cuûa maãu nhoû hôn hoaëc baèng 29875cm.
Giaûi :
()
−
≤
−
=〈
4
0.1
3029875
n
30X
P 29875 XP
= P (Z ≤ - 350)
= 0.062
Thí duï :
Moät nhaø saûn xuaát phuï tuøng xe oâtoâ cho bieát tuoåi thoï cuûa phuï tuøng xe tuaân theo luaät phaân
phoái chuaån vôùi soá trung bình laø 36,000 daëm vaø ñoä leäch chuaån laø 4,000 daëm. Ñoái vôùi moät
Gv. Cao Haøo Thi
5
maãu ñöôïc choïn moät caùch ngaãu nhieân vôùi côõ maãu laø 16 thì tuoåi thoï trung bình cuûa maãu laø
34,500 daëm. Neáu nhaø saûn xuaát noùi ñuùng thì xaùc suaát ñeå soá trung bình maãu nhoû hôn hoaëc
baèng giaù trò cuûa maãu ñaõ ño laø bao nhieâu.
Giaûi :
()
−
〈
σ
µ−
=〈
16
4000
0003650034
50034 ,,
X
P , X P
X
X
= P (Z < -1.5)
= 0.0668
Thí duï:
Giaû söû taäp hoïp chính tuaân theo phaân phoái chuaån vôùi soá trung bình laø 40 vaø phöông sai laø
100.
Phaân phoái xaùc suaát chuaån vôùi µ = 40, σ 2 = 100
Laáy 1,000 maãu ngaãu nhieân vôùi côõ maãu 5. Goïi X laø soá trung bình cuûa maãu. X tuaân theo
phaân phoái vôùi soá trung bình laø µ = 40 phöông sai
σ
2100
520
n==.
Laáy 1,000 maãu ngaãu nhieân vôùi côõ maãu 10. Goïi laø soá trung bình cuûa maãu. X tuaân theo
phaân phoái vôùi soá trung bình laø µ = 40, phöông sai
σ
2100
10 10
n==.
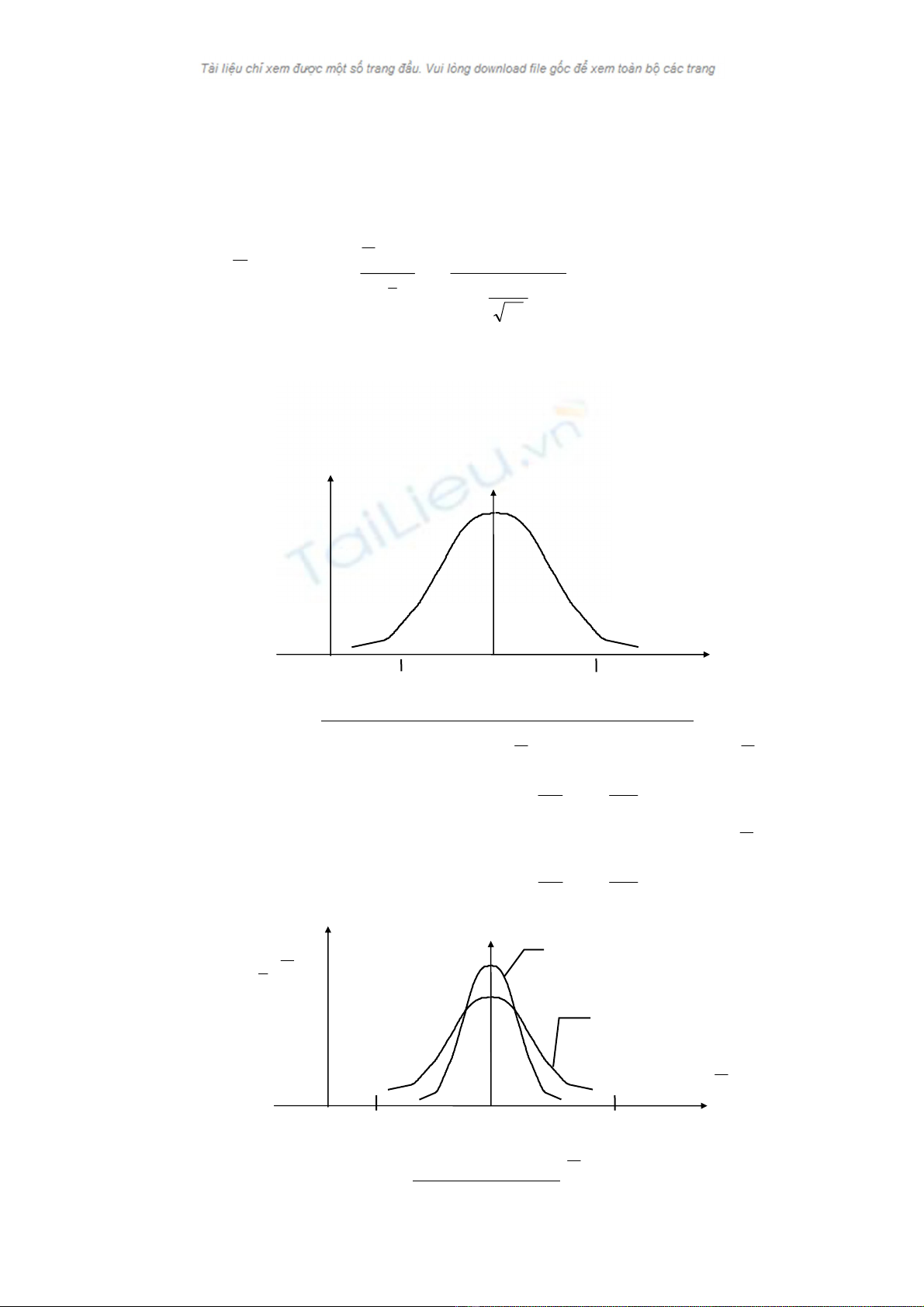
X
F(X)
60
40
Phaân
p
hoái maãu cuûa X
20
N = 10
60 Giaù trò cuûa bieán X
20 40
fx(x)
N = 5
X