G.V Cao Haoø Thi
Chöông 6
KIEÅM ÑÒNH GIAÛ THUYEÁT THOÁNG KEÂ
(Tests of Hypotheses)
Thoâng thöôøng ñoái vôùi tham soá • chöa bieát cuûa taäp hôïp chính ta coù theå ñöa ra nhieàu giaû
thuyeát veà •.
Vaán ñeà ñaët ra laø laøm theá naøo kieåm ñònh ñöôïc giaû thuyeát naøo thích hôïp vôùi caùc soá lieäu
cuûa maãu quan saùt ñöôïc (x1, x2, …, xn ).
6.1 NHÖÕNG KHAÙI NIEÄM VEÀ KIEÅM ÑÒNH GIAÛ THUYEÁT THOÁNG KEÂ
Giaû thuyeát thoáng keâ ( Statistical Hypothesis)
Laø moät giaû söû hay moät phaùt bieåu coù theå ñuùng, coù theå sai lieân quan ñeán tham soá cuûa moät
hay nhieàu taäp hôïp chính.
Giaû thuyeát khoâng (giaû thuyeát ñôn) vaø giaû thuyeát ngöôïc laïi (ñoái thuyeát)
(Null Hypothesis & Alternative Hypothesis)
Giaû thuyeát khoâng: laø söï giaû söû maø chuùng ta muoán kieám ñònh thöôøng ñöôïc kyù hieäu laø
Ho.
Giaû thuyeát ngöôïc laïi: Vieäc baùc boû giaû thuyeát khoâng seõ daãn ñeán vieäc chaáp nhaän giaû
thuyeát ngöôïc laïi. Giaû thuyeát ngöôïc laïi thöôøng ñöôïc kyù hieäu laø H1.
Ví duï
Kieám ñònh giaû thuyeát Ho: • ≥ •o coù theå •=•o
Vôùi H1: • < •o
Kieám ñònh giaû thuyeát Ho: • ≤ •o
Vôùi H1: • > •o
Kieåm ñònh giaû thuyeát Ho : • = •o
Vôùi H1: • ≠ •o
6.1.3 Caùc loaïi sai laàm trong vieäc kieåm ñònh giaû thuyeát thoáng keâ
Vieäc kieåm ñònh giaû thuyeát thoáng keâ coù theå phaïm phaûi 2 loaïi sai laàm
1.3.1 Sai laàm loaïi I (type I error)
Laø loaïi sai laàm maø chuùng ta phaïm phaûi trong vieäc baùc boû giaû thuyeát Ho khi
Ho ñuùng.
Xaùc suaát cuûa vieäc baùc boû Ho khi Ho ñuùng lkaø xaùc suaát cuûa sai laàm loaïi I vaø
ñöôïc kyù hieäu laø α
G.V Cao Haoø Thi
α = P ( baùc boû Ho / Ho ñuùng) = P(type I error)
α : coøn ñöôïc goïi laø möùc yù nghóa ( level of sigui ficance)
α = 0.05, 0,01 ,0,001 …
1.3.2 Sai laàm II (type II error)
Laø loai sai laàm maø chuùng ta phaïm phaûi khi khoâng baùc boû giaû thuyeát Ho khi
Ho sai.
Xaùc suaát cuûa vieäc khoâng baùc boû Ho khi Ho sai laø xaùc suaát cuûa sai laàm loaûi II vaø ñökôïc
kyù hieäu laøβ.
β = P (khoâng baùc boû Ho /Ho sai) = P(type II error)
Quyeát ñònh veà
giaû thuyeát khoâng Ho
Baûn chaát cuûa Ho
Ho ñuùng
Ho sai
Khoâng baùc boû ( chaáp nhaän )
Quyeát ñònh ñuùng
Prob = 1- α
P (khoâng baùc boû Ho / Ho) = 1-α
Sai laàm loaïi II
Prob = β
Baùc boû
Sai laàm loaïi I
Prob = α
(α = significance level of the test)
Quyeát ñònh ñuùng
Prob = 1 - β
(1 - β: power of the test)
naêng löïc cuaû kieåm ñònh
1.4 Mieàn baùc boû vaø mieàn chaáp nhaän
( rejection region & acceptance region )
Taát caû caùc giaù trò coù theå coù cuûa caùc ñaïi löôïng thoáng keâ trong kieåm ñònh coù theå
chia laøm 2 mieàn: mieàn baùc boû vaø mieàn chaáp nhaän.
- Mieàn baùc boû laø mieàn chöù caùc giaù trò laøm cho giaû thuyeát Ho bò baùc boû.
-Mieàn chaáp nhaän laø mieàn chöùa caùc giaù trò giuùp cho giaû thuyeát Ho khoâng bò baùc boû.
Trong thöïc teá khi Ho khoâng bò baùc boû cuøng nghóa laø noù ñöôïc chaáp nhaän.
Giaù trò chia ñoâi hai mieàn ñöôïc goïi laø giaù trò giôùi haïn ( Gitical value)
- Kieåm ñònh moät ñaàu vaø kieåm ñònh 2 ñaàu
(one – tailed test & two – tailed test)
Kieåm ñònh moät ñaàu
Khi giaû thuyeát ngöôïc laïi H1 coù tính chaát 1 phía (one – sided) thì vieäc kieåm ñònh ñöôïc
goïi laø kieåm ñònh 1 ñaàu.
Ví duï:
Ho: • = •o hay Ho: • = •o
G.V Cao Haoø Thi
H1: • > •o H1: • < •o
Kieåm ñònh hai ñaàu:
Khi giaû thuyeát ngöôïc laïi H1 coù tính chaát 2 phía( two – sided_ thì vieäc kieåm ñöôïc goïi laø
kieåm ñònh 2 ñaàu.
Ví duï
Ho: • = •o
H1: • ≠ •o
2. Caùc böôùc cuûa vieäc kieåm ñònh giaû thuyeát thoáng keâ
Goàm 6 böôùc:
Böôùc 1: Thaønh laäp giaû thuyeát Ho
Ví duï:
Ho: • = •o
Ho: • ≤ •o
Ho: • ≥ •o
Böôùc 2: Thaønh laäp giaû thuyeát H1
Ví duï:
H1: • < •o
H1: • > •o
H1: • ≠ •o
Böôùc 3: Xaùc ñònh möùc yù nghóa α
Böôùc 4: Choïn caùc tham soá thoáng keâ thích hôïp chko vieäc kieám ñònh vaø xaùc ñònh caùc
mieàn baùc boû, mieàn chaáp nhaän vaø giaù trò giôùi haïn.
Böôùc 5: Tính toaùn caùc giaù trò cuûa caùc tham soá thoáng keâ trong vieäc kieåm ñònh döïa treân
soá hieäu cuûa maãu ngaãu nhieân.
Böôùc 6: Ra quyeát ñònh: Neáu caùc giaù trò tính toaùn roài vaøo mieàn baùc boû Ho thì ra quyeát
ñònh baùc boû Ho. Ngöôïc laïi seõ chaáp nhaän Ho.
3. Kieåm ñònh giaù trò trung bình µ cuûa phaân phoái chuaån N (µ,δ2 ) khi ñaõ bieát δ2
Cho ( x1, x2 , …, xn) laø maãu ngaãu nhieân côõ n ñöôïc laáy töø taäp hoïp chính tuaân theo phaân
phoái chuaån N (µ,δ2 ) trong ñoù δ2 ñaõ bieát.
Vaán ñeà: Kieåm ñònh giaû thuyeát Ho : µ ≤ µο hay µ ≥ µο hay
µ = µο vôùi giaû thuyeát ngöôïc laïi H1: µ > µο hay µ < µο hay
µ ≠ µο . Söï kieåm ñònh coù möùc yù nghóa laø α.
Ta coù 3 tröôøng hôïp:
G.V Cao Haoø Thi
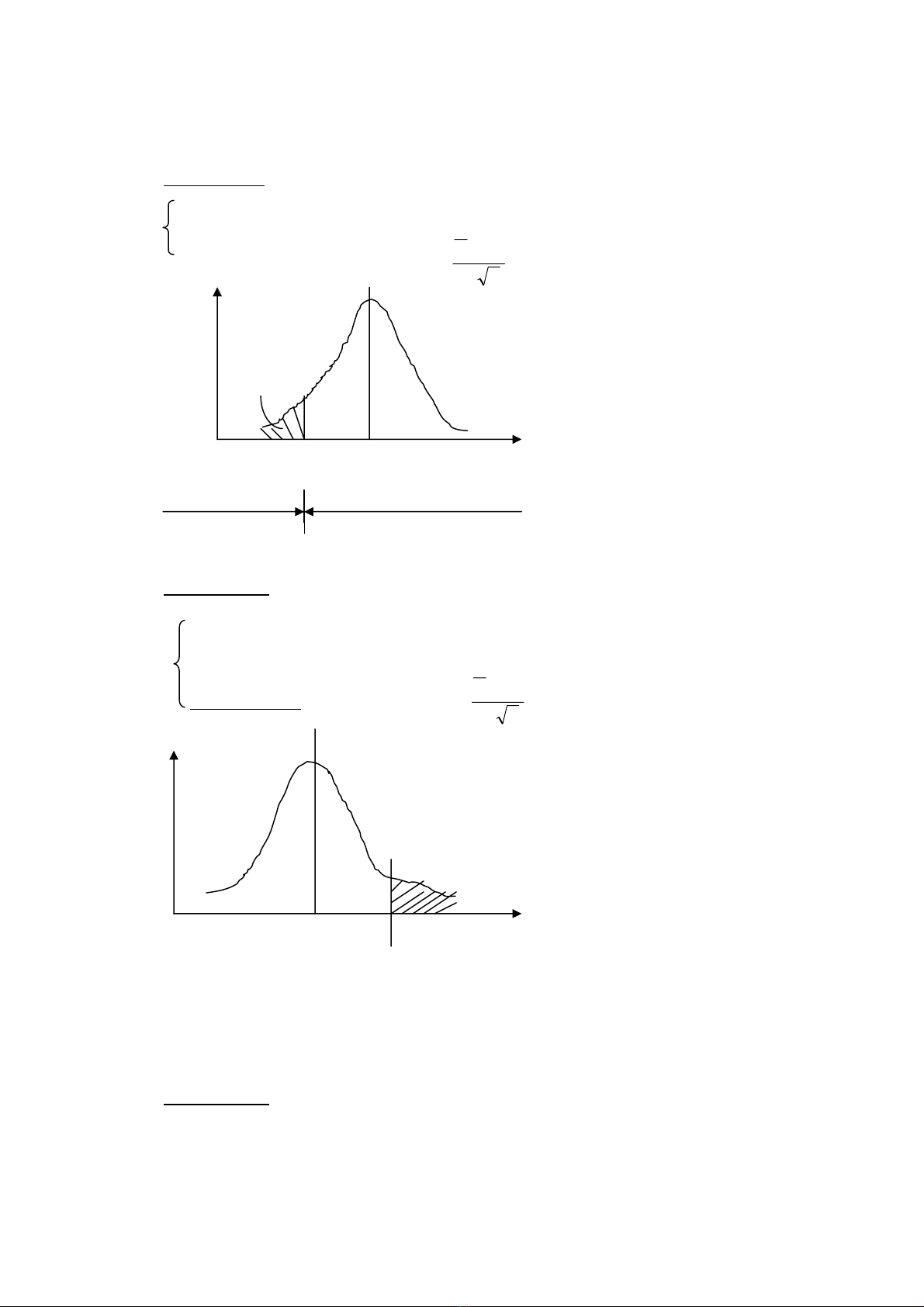
3.1 Tröôøng hôïp 1
Ho : µ = µο hay µο : µ ≥ µο
H1 : µ < µο
Mieàn baùc boû R: Baùc boû Ho neáu Σ = n/
X0
δ
µ− < − α
∑
3.2 Tröôøng hôïp 2:
Ho : 0
µ=µ hay Ho 0
µ
≤
µ
H
1 :µ > 0
µ
Mieàn baùc boû R: Baùc boû Ho neáu α
∑>
δ
µ−
=∑ n/
X0
3.3 Tröôøng hôïp 3:
α
α
∑
−α
∑
Fz
Mieàn baùc boû Ho Mieàn khoân
g
baùc boû Ho
G.V Cao Haoø Thi
Ho : 0
µ=µ
H
1 : 0
µ≠µ
Mieàn baùc boû R: Baùc boû Ho neáu
2
α
∑
>
∑
hay
2
α
∑
−
<
∑
Vôùi n/
X0
δ
µ−
=∑
Thí duï
Trong moät nhaø maùy baùnh keïo, moät maùy töï ñoäng saûn xuaát ra caùc thanh soâ coâ la vôùi
troïng löôïng qui ñònh 250g. Bieát raèng troïng löôïng caùc thanh soâ coâ la ñöôïc saûn xuaát ra coù
phaân boá chuaån N(µ,52). Trong moät ngaøy boä phaân kieåm tra kyõ thuaät choïn moät maãu ngaãu
nhieân goàm 16 thanh soâ coâ la vaø tính troïng löôïng trung bình cuûa chuùng ñöôïc 244g. Coù
theå khaúng ñònh maùy töï ñoäng saûn xuaát ra caùc thanh soâ coâ la coù troïng löôïng nhôù hôn qui
ñònh khoâng? Vôùi möùc yù nghóa α=0.05 kieåm ñònh giaû thuyeát thoáng keâ töông öùng.
Giaûi
1/ Ho : µ = 250g
2/ H1 : µ < 250g
3/ α = 0.05
4/ =∑=∑α05.0 16.45
- =∑α-1.645
5/ 8.4
16/5
250246
n/
X0−=
−
=
δ
µ−
=∑
=δ252 ⇒ δ = 5
n = 16
X = 244g , 0
µ = 250g
6/ Σ = -4.8 < - 05.0
∑ = -1,645
Ra quyeát ñònh : Baùc boû giaû thuyeát Ho
⇒ Chaáp nhaän H1 nghóa laø maùy töï ñoäng saûn xuaát soâ coâ la coù troïng löôïng nhoû hôn qui
ñònh.
⇒ Phaûi ñieàu chænh laïi maùy
Thí duï
Moät maùy khoan trong daây chuyeàn saûn xuaát duøng ñeå khkoan loã treân caùc baûn theùp. Khi
maùy khoan hoaït ñoäng ñuùng chöù naêng thieát keá ñöôøng kính caùc loã khoan seõ tuaân theo
phaân phoái chuaàn vôùi soá trung bình laø 2 inches vaø ñoä leäch chuaån laø 0,06 inches. Trong
quaù trình kieåm tra ñònh kyø xem maùy khoan coù hoaït ñoäng ñuùng hay khoâng, ngöôøi ta laáy
ño ngaãu nhieân caùc loã ñaõ khoan. Giaû söû ñoä leäch chuaån khoâng thay ñoåi. Maãu ngaãu nhieân