CHÖÔNG 5 ÖÔÙC LÖÔÏNG CAÙC THAM SOÁ THOÁNG KEÂ
(Estimation)
Khaùi nieäm chung:
- Xeùt moät taäp hoïp chính goâøm N bieán ngaãu nhieân X tuaân theo luaät phaân phoái coù haøm maät ñoä
xaùc suaát laø f (x,θ); trong ñoù θ laø caùc tham soá thoáng keâ cuûa taäp hoïp chính.
Thí duï:
• Trong phaân phoái nhò thöùc:
fx C
n
xx nx
(, ) ( )
θρρ
=−
−
1 => θ = ρ , θ ∈ [0 , 1]
• Trong phaân phoái poisson
fx e
x
x
(, ) !
θλ
λ
= => θ = λ θ > 0
• Trong phaân phoái chuaån
fx e
x
(, )
()
θπσ
µ
σ
=−−
1
22
2
2
2 => θ = (µ , σ2) , -∞ < µ < +∞
0 < σ2 < +∞
- Goïi {x1, x2,.... , xn} laø maãu ngaãu nhieân, côõ maãu n ñöôïc duøng laáy ra töø taäp hoïp chính tuaân
theo haøm maät ñoä xaùc suaát f (x,θ). ÔÛ ñaây daïng cuûa haøm f xem nhö ñaõ bieát coøn caùc tham soá thoáng keâ
θ cuûa taäp hoïp chính xem nhö chöa bieát.
Vaán ñeà ñaët ra ôû chöông trình naøy laø döïa vaøo caùc maãu quan saùt {x1,x2,...,xn} ta öôùc löôïng
xem giaù trò cuï theå cuûa θ baèng bao nhieâu (baøi toaùn ñoù goïi laø öôùc löôïng ñieåm ) hoaëc öôùc löôïng xem θ
naèm trong khoaûng naøo (baøi toaùn öôùc löôïng khoaûng).
1. ÖÔÙC LÖÔÏNG ÑIEÅM (Point Estimation)
1.1 Öôùc löôïng vaø giaù trò öôùc löôïng (estimator and estimate)
1.1.1 Öôùc löôïng (Estimatir) oâ haøm öôùc löôïng
• Laø bieán ngaãu nhieân hay caùc tham soá thoáng keâ cuûa maãu ñöôïc duøng ñeå öôùc löôïng caùc tham soá
thoáng keâ chöa bieát cuûa taäp hôïp chính.
• Öôùc löôïng cuûa tham soá thoáng keâ θ cuûa taäp hoïp chính ñöôïc kyù hieäu laø
θ
∧.
• Döïa vaøo maãu {x1,x2...,xn} ngöôøi ta laäp ra laøm
θ
∧ =
θ
∧ (x1,x2,....,xn) ñeå öôùc löôïng cho θ.
θ
∧ ñöôïc
goïi laø haøm öôùc löôïng cuûa θ hay goïi taét laø öôùc löôïng cuûa θ.
θ
∧ chæ phuï thuoäc vaøo giaù trò quan saùt x1, x2, ... ,xn chöù khoâng phuï thuoäc vaøo caùc tham chöa soá
bieát θ cuûa taäp hoïp chính.
1.1.2 Giaù trò öôùc löôïng (estimate) hay coøn goïi laø giaù trò öôùc löôïng ñieåm (point estimate)
• Laø giaù trò cuï theå cuûa öôùc löôïng
θ
∧ vaø ñöôïc xem nhö giaù trò öôùc löôïng cuûa tham soá thoáng keâ θ cuûa
taäp hoïp chính.
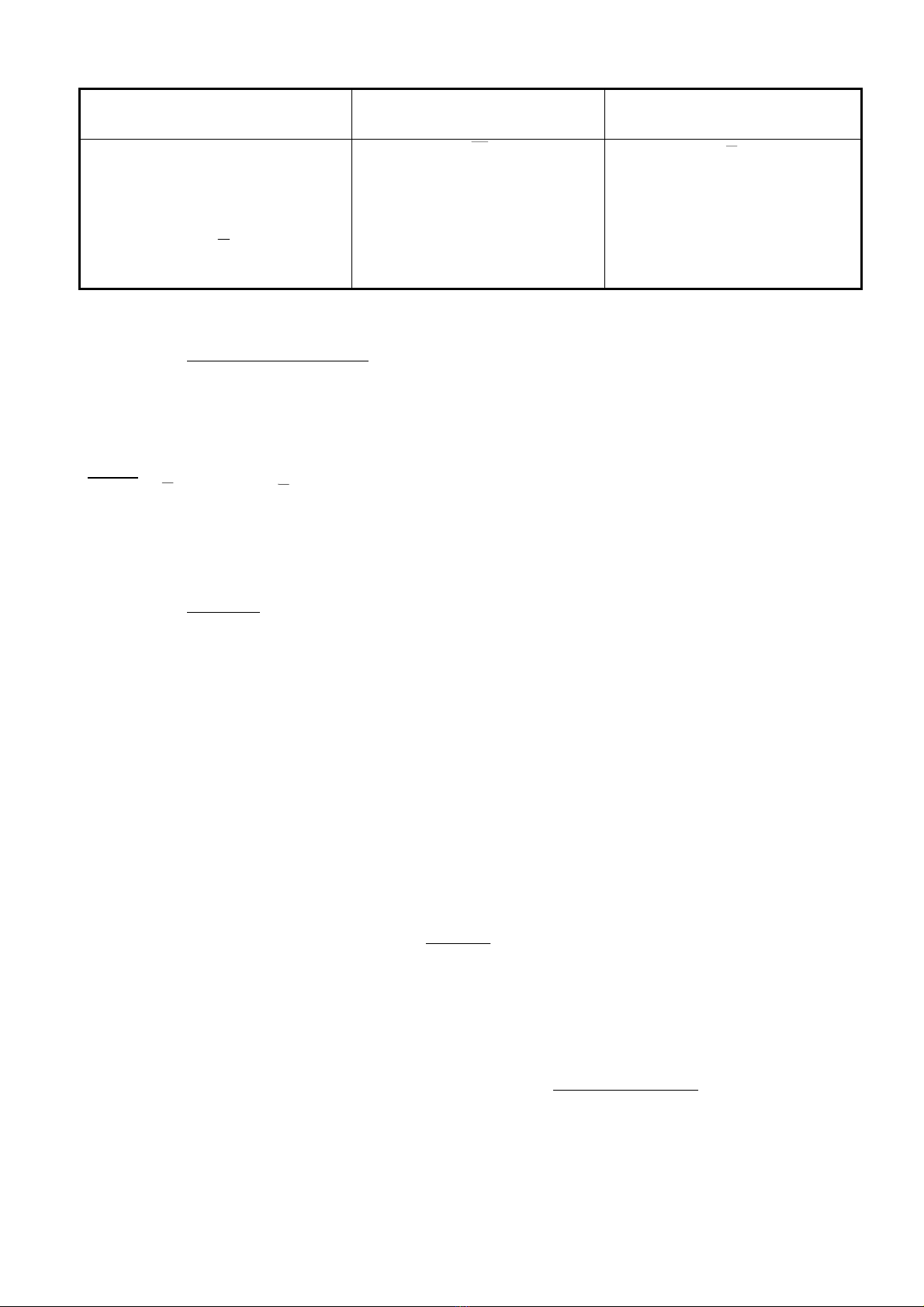
Tham soá thoáng keâ vaø taäp hoïp
chính (population patameter)
Öôùc löôïng
(Estimation)
Giaù trò öôùc löôïng Estimate
(Point estimate)
Soá trung bình µx
Phöông sai σx2
Ñoä leäch chuaån σx
Trò soá p f
x
n
=
p
X
Sx2
Sx
f
∧
px
∧
x
Sx2
Sx
f
∧
px
∧
1.2 Öôùc löôïng khoâng cheäch: (Unbiased estimators)
1.2.1 Öôùc löôïng khoâng cheäch:
• Öôùc löôïng θ ñöôïc goïi laø öôùc löôïng khoâng cheäch cuûa tham soá thoáng keâ θ neáu kyø voïng cuûa
θ
∧ laø
θ.
E (
θ
∧) = θ
Thí duï
E(X) = µx => X laø öôùc löôïng khoâng cheäch cuûa µx
E(Sx2) = σx2 => Sx2 laø öôùc löôïng khoâng cheäch cuaû σx2
E ( f
∧) = p => f
∧ laø öôùc löôïng khoâng cheäch cuûa p
12.2. Ñoä cheäch (The bias)
• Goïi
θ
∧ laø öôùc löôïng cuûa θ.
Bias(
θ
∧) = E (
θ
∧) - θ
• Ñoái vôùi öôùc löôïng khoâng cheäch => Bias = ñoä cheäch = 0
1.3 Öôùc löôïng hieäu quaû toát nhaát:
• Goïi
θ
∧
1 vaø
θ
∧
2 laø 2 öôùc löôïng khoâng cheäch cuûa θ döïa treân soá löôïng cuûa maãu quan saùt gioáng
nhau.
*
θ
∧
1 ñöôïc goïi laø hieäu quaû hôn
θ
∧
2 neáu
Var (
θ
∧
1) < Var (
θ
∧
2)
* Hieäu quaû töông ñoái giöõa hai öôùc löôïng laø tæ soá giöõa 2 phöông sai cuûa chuùng.
Hieäu quaû töông ñoái = Var
Var
()
()
θ
θ
2
1
∧
∧
(Relative efficency)
• Neáu
θ
∧ laø öôùc löôïng khoâng cheäch cuûa θ vaø neáu khoâng coù moät öôùc löôïng khoâng cheäch naøo coù
phöông sai nhoû hôn phöông sai cuûa
θ
∧ thì
θ
∧ ñuôïc goïi laø öôùc löôïng toát nhaát (best estimator) hay
θ
∧ coøn goïi laø öôùc löôïng khoâng cheäch coù phöông sai nhoû nhaát cuûa θ (minimum variance unbiased
estimator of θ)
1.4 Sai soá bình phöông trung bình (men spuared eveor) MSE
• Sai soá bình phöông trung bình cuûa öôùc löôïng
θ
∧ ñöôïc ñònh nghóa nhö sau:
MSE(
θ
∧) = E [(
θ
∧ - θ)2]
Ngöôøi ta chöùng minh ñöôïc raèng:
MSE (
θ
∧) = Var(
θ
∧) + [θ - E (
θ
∧)]2
MSE (
θ
∧) = Var (
θ
∧) + [ Bias(
θ
∧)]2
• Neáu
θ
∧ laø öôùc löôïng khoâng cheäch ta coù
Bias(
θ
∧) = 0
=> MSE (
θ
∧) = Var (
θ
∧)
1.5 Öôùc löôïng nhaát quaùn vöõng (Consistent estimators)
θ
∧
n =
θ
∧ (x1, x2,... xn) goïi laø öôùc löôïng vöõng cuûa θ neáu vôùi moïi ε > 0 ta coù:
lim P( |
θ
∧
n - θ | ≤ ε ) = 1]
n - ∞
töùc laø daõy
θ
∧
n hoäi tuï theo xaùc suaát tôùi θ khi n -> ∞
2. ÖÔÙC LÖÔÏNG KHOAÛNG (Interal estimation)
2.1 Khoaûng tin caäy (Confidence interval)
2.1.1. Öôùc löôïng khoaûng vaø giaù trò öôùc löôïng khoaûng (interval estimator and interval
estimate).
* Öôùc löôïng khoaûng:
Öôùc löôïng khoaûng ñoái vôùi tham soá thoáng keâ cuûa taäp hoïp chính θ laø moät quy taéc döïa treân
thoâng tin cuûa maãu ñeå xaùc ñònh mieàn (range) hay khoaûng (interval) maø tham soá θ haàu nhö naèm
trong ñoù.
* Gía trò öôùc löôïng khoaûng: laø giaù trò cuï theå cuûa mieàn hay khoaûng maø tham soá θ naèm trong
ñoù.
2.1.2 Khoaûng tin caäy vaø ñoä tin caäy (Confidence interval and level of confidence)
Goïi θ laø tham soá thoáng keâ chöa bieát. Giaû söû döïa treân thoâng tin cuûa maãu ta coù theå xaùc ñònh
ñöôïc 2 bieán ngaãu nhieân A vaø B sao cho
P (A < θ < B) = 1 - α vôùi 0 < α < 1
• Neáu giaù trò cuï theå cuûa bieán ngaãu nhieân A vaø B laø a vaø b thì khoaûng (a,b) töø a ñeán b ñöôïc goïi laø
khoaûng tin caäy cuûa θ vôùi xaùc suaát la (1 - α)
• Xaùc suaát (1 - α) ñöôïc goïi laø ñoä tin caäy cuûa khoaûng.
Ghi chuù:
• Trong thöïc teá, ñoä tin caäy (1 -α) do nhaø thoáng keâ choïn theo yeâu caàu cuûa mình, thoâng thöôøng ñoä
tin caäy ñöôïc choïn laø 0,90; 0,95; 0,99...
• α laø xaùc suaát sai laàm khi choïn khoaûng tin caäy (a, b)
2.2 Khoaûng tin caäy ñeán vôùi soá trung bình cuûa phaân phoái chuaån trong tröôøng hôïp ñaõ bieát
phöông sai cuûa taäp hoïp chính:
Nghóa laø ñi tìm öôùc löôïng cuûa µ trong N (µ, σx2) khi ñaõ bieán σx2
2.2.1 Ñieåm phaàn traêm giôùi haïn treân Z (Upper percentage cut off point)
Goïi Z laø bieán ngaãu nhieân chuaån hoùa vaø α laø soá baát kyø sao cho 0 <α < 1
Zα laø ñieåm phaàn traêm giôùi haïn treân neáu.
P (Z > Zα ) = α
Ghi chuù:
• P (Z > Zα) = FZ (zα) = 1 - α
Hình 2 (p5)
• P (-Zα/2 < Z < Zα/2) = 1 - α
Chöùng minh:
P(Z > Zα/2 ) =
α
2
Do tính ñoái xöùng => P (-Zα/2 < Z < Zα/2) = 1 -
α
2 -
α
2 = 1 - α
P (Z < -Zα/2) =
α
2
Hình 3 (P5)
2.2.2 Khoaûng tin caäy cuûa µ trong N(µ,σx2) khi ñaõ bieát σx2
Giaû söû ta coù maãu ngaãu nhieân vôí côõ maãu n töø phaân phoái chuaån N(µ,σx2). Neáu σz2 ñaõ bieát vaø
soá trung bình maãu coù giaù trò trung bình taäp hoïp chính ñöôïc tính bôûi.
x
Z
nx
Z
n
xx
−−
−<<+
αα
σ
µ
σ
//22
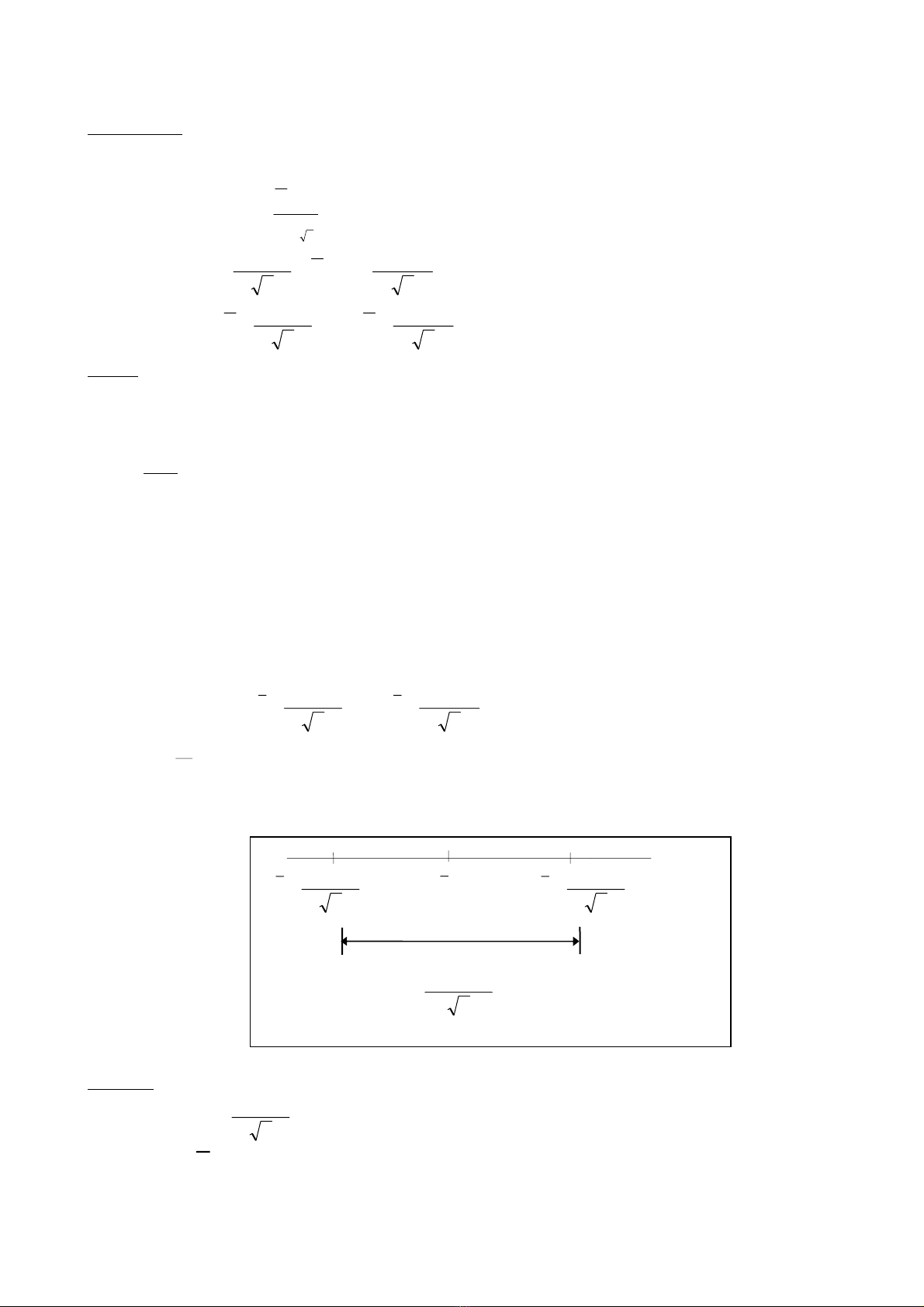
Trong ñoù Zα/2 laø soá coù P (Z > zα/2) = α/2 vôùi Z laø bieán ngaãu nhieân chuaån chuaån hoùa.
Chöùng minh:
Ta coù:
P ( - Zα/2 < Z < Zα/2) = 1 - α
P (-Zα/2 <XZ
xn
−<
µ
σα
/
/)
2= 1 - α
P(
−<−<
Z
nX
Z
n
xX
αα
σ
µ
σ
//
)
22
= 1 - α
P (
X
Z
nX
Z
n
xX
−<<+
αα
σ
µ
σ
//
)
22
= 1 - α
Thí duï:
Giaû söû troïng löôïng cuûa caùc hoïc sinh lôùp 2 tuaân theo phaân phoái chuaån vôùi ñoä leäch chuaån
1,2kg. Maãu ngaãu nhieân goàm 25 hoïc sinh coù trung bình laø 19,8kg. Tìm khoaûng tin caäy 95% ñoái vôùi
troïng löôïng trung bình cuûa taát caû hoïc sinh lôùp 2 trong 1 tröôøng.
Giaûi:
Ta coù 100 (1 - α) = 95
=> α = 0.05
=> Z
α/2 = Z 0.025
=> P(Z > Z0.025) = 0.025
P(Z < Z0.025) = FZ (Z0.025) = 1 - 0.025 = 0.975
Tra baûng ta coù:
Z
0.025 = 1.96
Khoaûng tin caäy 95% ñoái vôùi soá trung bình taäp chính µ seõ laø
x
Z
nx
Z
n
xX
−<<+
αα
σ
µ
σ
//22
Vôùi x = 19,8 kg σx = 1,2 kg x = 25 Zα/2 = 1,96
=> 19,33 < µ < 20,27
Ghi chuù:
a)
ε
σ
α
=
Z
n
x/2 goïi laø ñoä chính xaùc cuûa öôùc löôïng hay dung sai
b) x laø trung taâm cuûa khoaûng tin caäy vôùi beà roäng cuûa khoaûng tin caäy cuûa µ laø
x
Z
n
x
−=
α
σ
/,
219 33
x
= 19,8 x
Z
n
x
+=
α
σ
/,
220 83
22
Z
n
x
α
σ
/