Ch ng IIIươ
Mô hình h i qui tuy n tính đ nồ ế ơ
( mô hình h i qui hai bi n)ồ ế
1
Y
Mô hình h i qui đ nồ ơ
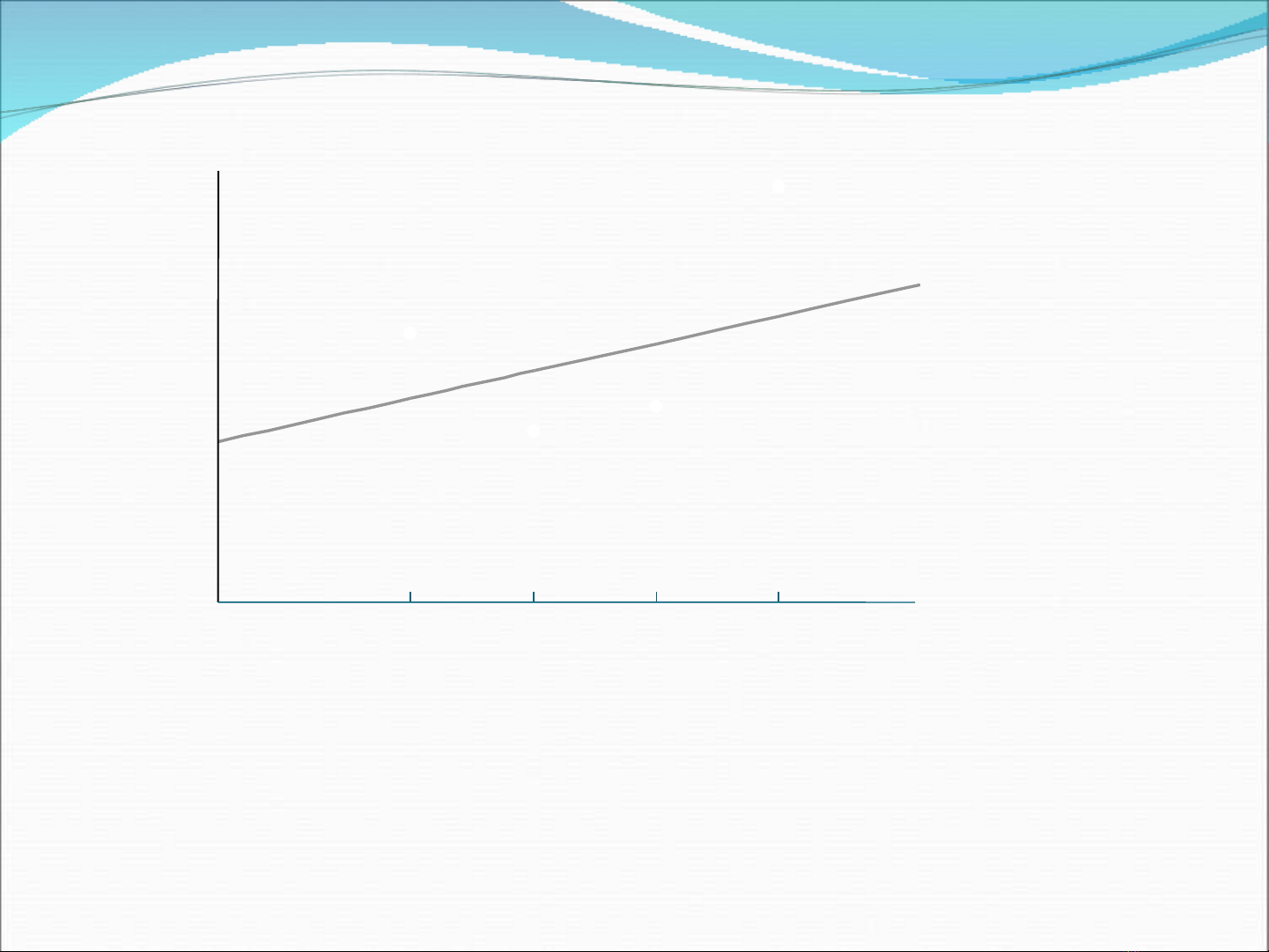
Gi s r ng bi n y là m t hàm tuy n tính c a bi n X v i các tham s ch a bi t ả ử ằ ế ộ ế ủ ế ớ ố ư ế b1 và b2 mà
chúng ta mu n c tínhố ướ
XY 21
ββ
+=
b1
X
X1X2X3X4
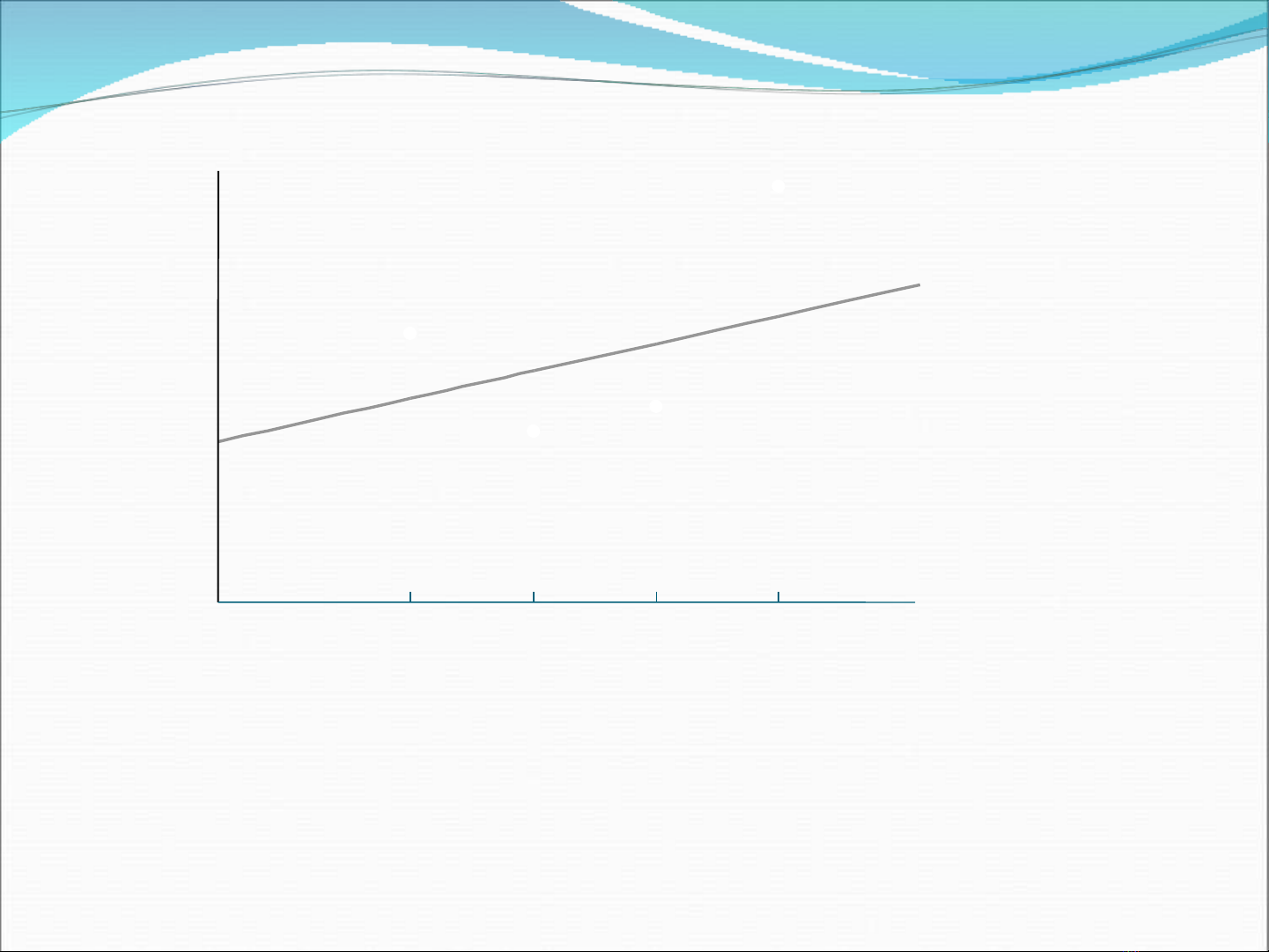
Gi s r ng chúng ta có b n quan sát v i các giá tr c a X đ c ch ra nh trênả ử ằ ố ớ ị ủ ượ ỉ ư
Mô hình h i qui đ nồ ơ
2
XY 21
ββ
+=
b1
Y
X
X1X2X3X4
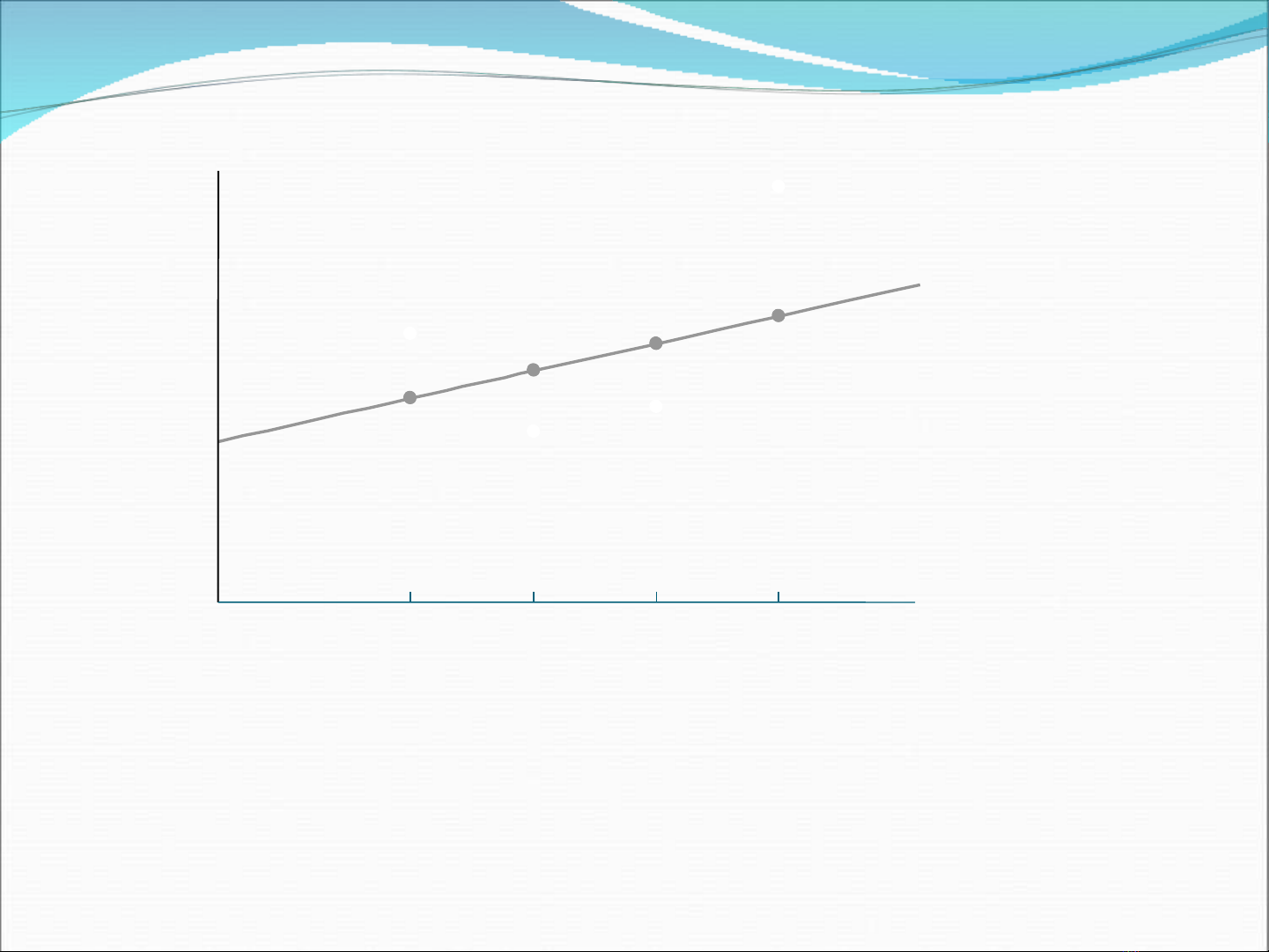
N u m i quan h gi a hai y u t là chính xác, các quan sát s n m trên đ ng th ng và chúng ra ế ố ệ ữ ế ố ẽ ằ ườ ẳ
s không có v n đ gì khi chúngta đ có m t c tính chính xác v các tham sẽ ấ ề ể ộ ướ ề ố b1 và b2.
Q
1
Q
2
Q
3
Q
4
Mô hình h i qui đ nồ ơ
3
XY 21
ββ
+=
b1
Y
X
X1X2X3X4
P4
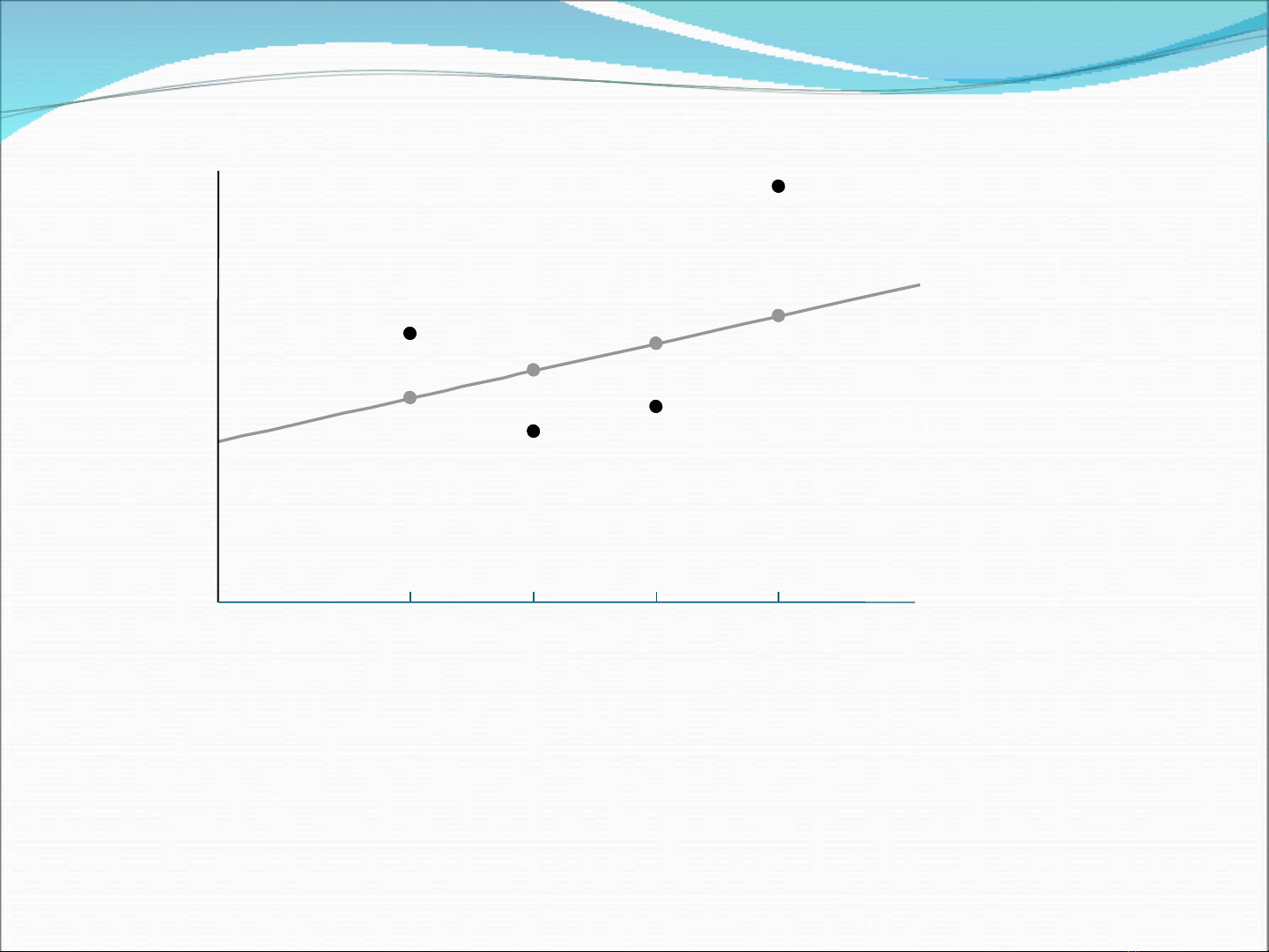
Trong th c th , ph n l n các m i quan h kinh t là không chính xác và các giá tr th c th c a Y ự ế ầ ớ ố ệ ế ị ự ế ủ
khác bi t so v i các gia tr t ng ng trên đ ng th ngệ ớ ị ươ ứ ở ườ ẳ
P3
P2
P1
Q
1
Q
2
Q
3
Q
4
Mô hình h i qui đ nồ ơ
4
XY 21
ββ
+=
b1
Y
X
X1X2X3X4