TR NG THPT C M BÁ TH C ƯỜ Ầ ƯỚ CHUYÊN Đ CHUY N Đ NG CỀ Ể Ộ Ơ
THCS
TT ÔN LUY N CH T L NG CAO Ệ Ấ ƯỢ
A/ Tóm t t ki n th c ắ ế ứ
1) Chuy n đ ng c h c ể ộ ơ ọ
Đ nh nghĩa:ị CĐ c h c là s thay đ i v trí c a m t v t so v i m t v t khác đ c ch n làmơ ọ ự ổ ị ủ ộ ậ ớ ộ ậ ượ ọ
m c.ố
Chuy n đ ng và đ ng yên có tính t ng đ i tùy thu c vào v t đ c ch n làm m c. Ng i taể ộ ứ ươ ố ộ ậ ượ ọ ố ườ
th ng ch n nh ng v t g n v i m t đ t làm v t m c.ườ ọ ữ ậ ắ ớ ặ ấ ậ ố
2) V n t c:ậ ố
* V n t c đ c tr ng cho s nhanh hay ch m c a chuy n đ ng ậ ố ặ ư ự ậ ủ ể ộ
* Công th c: ứ
t
S
=
υ
(1) - Là quãng đ ng đi đ c trong 1 giâyườ ượ
* Đ n v v n t c ph thu c vào đ n v c a th i gian (t) và đ n v c a quãng đ ng (S); km/h;ơ ị ậ ố ụ ộ ơ ị ủ ờ ơ ị ủ ườ
m/s.
* 1m/s = 3,6 km/h; 1Km/h = 0,28 m/s
* V n t c là đ i l ng véct . Véc t v n t c cóậ ố ạ ượ ơ ơ ậ ố
+ G c đ t t i v t ố ặ ạ ậ
+ Ph ng trùng v i ph ng chuy n đ ng ươ ớ ươ ể ộ
+ Chi u trùng v i chi u chuy n đ ng ề ớ ề ể ộ
+ Chi u dài t l v i đ l n: ề ỉ ệ ớ ộ ớ
t
S
=
υ
3) Chuy n đ ng th ng đ u. ể ộ ẳ ề
a. Đ nh nghĩaị : Chuy n đ ng th ng đ u là chuy n đ ng trong đó v t đi nh ng qu ng đ ngể ộ ẳ ề ể ộ ậ ữ ả ườ
b ng nhau b t kỳ thì m t kho ng th i gian là nh nhau.ằ ấ ấ ả ờ ư
Trong chuy n đ ng th ng đ u véc t v n t c là không đ i c v chi u và đ l n.ể ộ ẳ ề ơ ậ ố ổ ả ề ề ộ ớ
b.Qu ng đ ng chuy n đ ng trong CĐ th ng đ uả ườ ể ộ ẳ ề
Bi u th cể ứ : S = v.t .
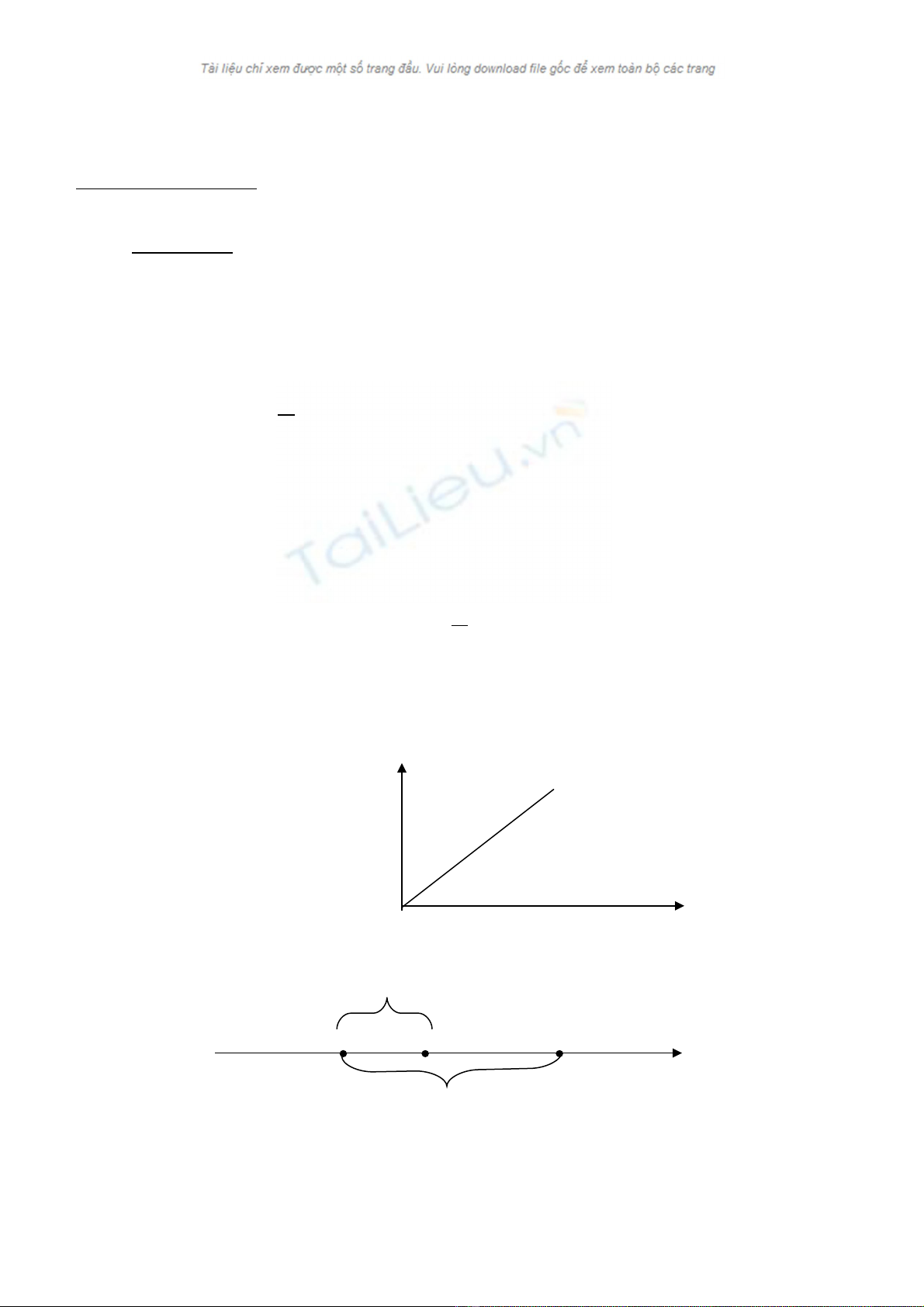
Đ th : ồ ị
Chú ý: Đ th là đ ng th ng đi qua g c t a đ và h ng lênồ ị ườ ẳ ố ọ ộ ướ
c. T a đ c a v t chuy n đ ng th ng đ uọ ộ ủ ậ ể ộ ẳ ề
Xét chuy n đ ng th ng đ u c a m t v t trên đ ng th ng AB. ể ộ ẳ ề ủ ộ ậ ườ ẳ
G n vào đ ng th ng AB m t tr c t a đ . Có O tùy ý, ph ng trùng v i AB, chi u tùy ý(Giắ ườ ẳ ộ ụ ọ ộ ươ ớ ề ả
thi t ch n là t A đ n B)ế ọ ừ ế
Gi s t i th i đi m t=tả ử ạ ờ ể 0 v t đang v trí Mậ ở ị 0 và có t a đ xọ ộ 0. T đây v t chuy n đ ng th ngừ ậ ể ộ ẳ
đ u v i v n t c về ớ ậ ố . th i t b t kỳ v t v trí MỞ ờ ấ ậ ở ị t có t a đ x. ọ ộ
Nhi m v c a v t lý là tìm m t ph ng trình mô t s bi n đ i t a đ x c a v t theo th i gian.ệ ụ ủ ậ ộ ươ ả ự ế ổ ọ ộ ủ ậ ờ
Ph ng trình đó g i là ph ng trình t a đ hay ph ng trình chuy n đ ng c a v t.ươ ọ ươ ọ ộ ươ ể ộ ủ ậ
Ta xây d ng ph ng trình:ự ươ
S(m, km)
t(s, h)
O
x
OA BM0Mt
t0t
x
x0
T hình v ta có: x = xừ ẽ 0 + M0Mt có M0Mt = v.(t-t0) v y ta đ cậ ượ
x = x0 + v.(t-t0) (2)
Chú ý
1./V i xớ0: N u thì xế0>0
N u thì xế0<0
2./V i v n t c v: N u v t chuy n đ ng cùng chi u d ng thì v>0 ng c l i v<0ớ ậ ố ế ậ ể ộ ề ươ ượ ạ
3./ t0 là th i đi m khi ta b t đ u kh o sát chuy n đ ng c a v t ta có th tùy ch n giá tr c a nó.ờ ể ắ ầ ả ể ộ ủ ậ ể ọ ị ủ
Thông th ng ch n tườ ọ 0=0 khi đó ph ng trình chuy n đ ng c a v t là:ươ ể ộ ủ ậ
x = x0 + vt (3)
Đ th t a đ - th i gian c a v t chuy n đ ng th ng đ uồ ị ọ ộ ờ ủ ậ ể ộ ẳ ề
T ph ng trình (3) ta th y x bi n thiên theo hàm b c nh t đ i v i th i gian t do v y đ th t aừ ươ ấ ế ậ ấ ố ớ ờ ậ ồ ị ọ
đ - th i gian là m t đ ng th ng.ộ ờ ộ ườ ẳ
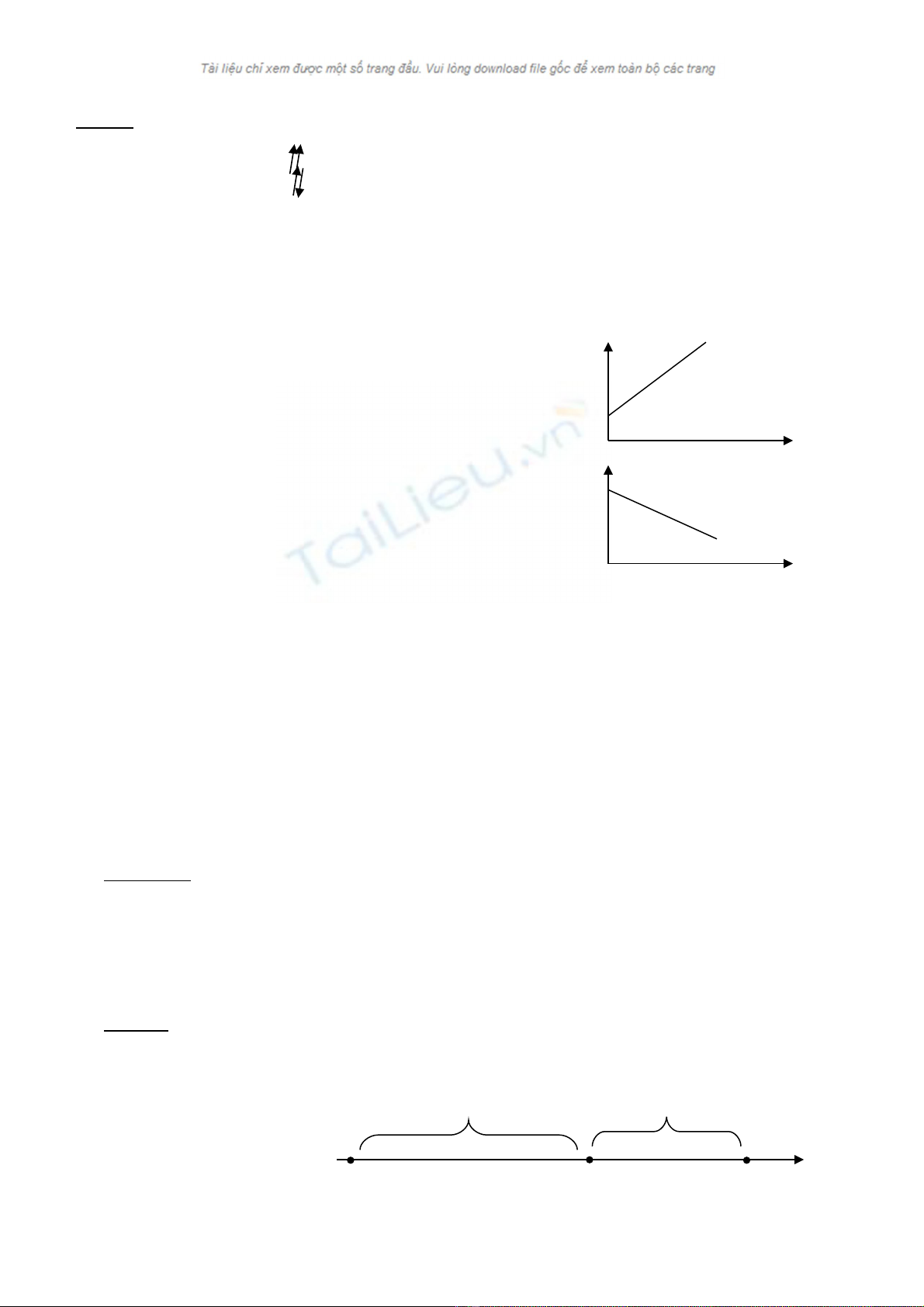
Xét 2 chuy n đ ngể ộ
- Chuy n đ ng cùng chi u d ng ta có đ th là: ể ộ ề ươ ồ ị
-Chuy n đ ng ng c chi u d ng ta có đ th là: ể ộ ượ ề ươ ồ ị
4. Chuy n đ ng th ng không đ uể ộ ẳ ề
Đ nh nghĩa:ị Là chuy n đ ng trên m t đ ng th ng song có v n t c thay đ i.ể ộ ộ ườ ẳ ậ ố ổ
Trong chuy n đ ng th ng bi n đ i ta ch có th nói t i v n t c trung bình c a v t.ể ộ ẳ ế ổ ỉ ể ớ ậ ố ủ ậ
Vtb= = = =
5. Tính t ng đ i c a chuy n đ ngươ ố ủ ể ộ
- Đ i v i các v t đ c ch n làm m c khác nhau v n t c c a m t v t là khác nhau.ố ớ ậ ượ ọ ố ậ ố ủ ộ ậ
- M t s tr ng h p đ c bi t:ộ ố ườ ợ ặ ệ
G i Vọ13 là v n t c c a v t (1) đ i v i v t (3), Vậ ố ủ ậ ố ớ ậ 23 là v n t c c a v t (2) đ i v i v t (3)ậ ố ủ ậ ố ớ ậ
N u: Hai v t chuy n đ ng cùng h ng(cùng ph ng, cùng chi u) thì v n t c c a v t (1) đ i v iế ậ ể ộ ướ ươ ề ậ ố ủ ậ ố ớ
v t (2) là: Vậ12 = |V13 -V23|(tr tuy t đ i vì ch a bi t v n t c c a v t nào đ i v i v t (3) là l n h n). ị ệ ố ư ế ậ ố ủ ậ ố ớ ậ ớ ơ
N u: Hai v t chuy n đ ng ng c h ng(Cùng ph ng nh ng ng c chi u) thì v n t c c a v t (1)ế ậ ể ộ ượ ướ ươ ư ượ ề ậ ố ủ ậ
đ i v i v t (2) là: Vố ớ ậ 12 = V13 +V23
B. Bài t p ậ
Các d ng bài t p th ng g pạ ậ ườ ặ
1./Bài toán xác đ nh v trí và th i đi m các v t g p nhau ho c th i đi m và v trí các v t cách nhauị ị ờ ể ậ ặ ặ ờ ể ị ậ
m t kho ng cho tr c.ộ ả ướ
2./Bài toán liên qua đ n tính t ng đ i c a chuy n đ ng.ế ươ ố ủ ể ộ
3./ Bài toán đ thồ ị
4./Bài toán tính v n t c TBậ ố
D ng 1.ạ Bài toán xác đ nh v trí và th i đi m các v t g p nhau ho c th i đi m và v trí các v tị ị ờ ể ậ ặ ặ ờ ể ị ậ
cách nhau m t kho ng cho tr c.ộ ả ướ
I. Ph ng pháp gi i:ươ ả
Có hai cách gi i c b n đ i v i d ng toán nàyả ơ ả ố ớ ạ
Cách 1. Dùng công th c đ ng đi.ứ ườ
Hai v t g p nhau khi: Sậ ặ 1+S2 = AB t đó suy ra k t quừ ế ả
x
A B
S1=V1.t S2=V2.t
C
Cách 2. Dùng ph ng trình t a đươ ọ ộ
V i cách này thì khi hai v t g p nhau chúng ph i có t a đ nh nhau nghĩa là:ớ ậ ặ ả ọ ộ ư
X1=X2 t đó suy ra k t quừ ế ả
II. Bài t p áp d ngậ ụ
Bài t p s 1: ậ ố Cùng m t lúc t i hai đi m Avà B Cách nhau 25Km, hai xe cùng xu t phát , cùng điộ ạ ể ấ
v nhau và cùng chuy n đ ng đ u v i v n t c l n l t là ề ể ộ ề ớ ậ ố ầ ượ
hKm
A
/20
=
υ
;
hKm
B
/30
=
υ
. H iỏ
hai xe g p nhau lúc nào ? đâu? Bi t th i gian khi b t đ u xu t phát là tặ Ở ế ờ ắ ầ ấ 0= 7gi 30 phút.ờ
Bài t p s 2:ậ ố M t v t xu t phát t A chuy n đ ng th ng đ u v B cách A 630m v i v n t cộ ậ ấ ừ ể ộ ẳ ề ề ớ ậ ố
13m/s. Cùng lúc đó , m t v t khác chuy n đ ng t B v A. Sau 35giây hai v t g p nhau . Tính v n t cộ ậ ể ộ ừ ề ậ ặ ậ ố
c a v t th hai và v trí hai v t g p nhau .ủ ậ ứ ị ậ ặ
Bài t p s 3. ậ ố An và Bình cùng kh i hành t m t n i. An đi b v i v n t c 4km/h và kh i hànhở ư ộ ơ ộ ớ ậ ố ở
tr c Bình 2h. Bình đi xe đ p và đu i theo An v i v n t c 12km/h. H i:ướ ạ ổ ớ ậ ố ỏ
a) Sau bao lâu k t lúc Bình kh i hành thì Bình đu i k p An ? Khi đó c hai cách n i kh i hànhể ừ ở ổ ị ả ơ ở
bao xa.
b) Sau bao lâu k t lúc Bình kh i hành thì Bình và An cách nhau 4 km.ể ừ ở
Bài t p s 4.ậ ố T i hai đ u A , B c a m t đo n đ ng dài 5km có 2 ng i kh i hành cùng m tạ ầ ủ ộ ạ ườ ườ ở ộ
lúc ch y ng c chi u nhau v i v n t c vạ ượ ề ớ ậ ố A=12km/h , vB= 8km/h. M t con chó cùng xu t phát và ch yộ ấ ạ
cùng chi u v i A v i v n t c 16km/h. Trên đ ng khi g p ng i B nó l p t c quay l i và khi g pề ớ ớ ậ ố ườ ặ ườ ậ ứ ạ ặ
ng i A nó l i l p t c quay l i và c ch y đI ch y l i nh th cho đ n khi c 3 cùng g p nhau ườ ạ ậ ứ ạ ứ ạ ạ ạ ư ế ế ả ặ
a, Tính t ng đo n đ ng mà chó đã ch y ổ ạ ườ ạ
b, Hai ng i g p nhau đâu?ườ ặ ở
Gi iả
SA = vA.t = 12t
SB = vB.t = 8t
SC = vCt = 16t
Khi 3 v t g p nhau thì:ậ ặ
SA + SB = AB = 5
(vA + vB)t = 5 => t = 0,25h
=> SC = 16.0,25 = 4km
Thay t = 0,25 vào (1) ta có:
SA = vA.t = 12t =3 km
KL: t ng đo n đ ng mà chó đã ch y: 4kmổ ạ ườ ạ
Hai ng i g p nhau cách A 3 kmườ ặ
TR NG THPT C M BÁ TH C CHUYÊN Đ CHUY N Đ NG C THCSƯỜ Ầ ƯỚ Ề Ể Ộ Ơ
TT ÔN LUY N CH T L NG CAO (bài t p v nhà)Ệ Ấ ƯỢ ậ ề
x
A B
x1
x2
O
C