CHUYÊN Đ HÀM S B C HAIỀ Ố Ậ
M C L CỤ Ụ
1
CHUYÊN Đ HÀM S B C HAIỀ Ố Ậ
Danh sách các kí hi u s d ngệ ử ụ
Ký hi uệ
Max Min
Đc làọKhác Thu cộT ng đngươ ươ Suy ra Giá tr l n nh tị ớ ấ Giá tr nh nh tị ỏ ấ
Danh sách các tài li u tham kh oệ ả
+ Sách giáo khoa Toán 9 t p 2ậ- NXB GD
+ Nâng cao và phát tri n Toán 9 ể- Vũ H u Bìnhữ
+ Bài t p và câu h i tr c nghi m Toán 9ậ ỏ ắ ệ - Phan L u Biênư
+ B i d ng năng l c t h c Toán 9ồ ưỡ ự ự ọ - PGS – TS Đng Đc Tr ngặ ứ ọ
2
CHUYÊN Đ HÀM S B C HAIỀ Ố Ậ
HÀM S y = axỐ2
PH NG TRÌNH B C HAI M T NƯƠ Ậ Ộ Ẩ
A. KI N TH C C B N:Ế Ứ Ơ Ả
A. Hàm s y = axố2 (a 0)
a) Tính ch t ấ
Hàm s y = axố2 (a 0) đc xác đnh vói m i giá tr c a ượ ị ọ ị ủ
a > 0. Hàm s đng bi n khi x > 0; ngh ch bi n khi x < 0ố ồ ế ị ế
y = 0 là giá tr nh nh t c a hàm s , đt đc khi x = 0ị ỏ ấ ủ ố ạ ượ
a < 0. Hàm s đng bi n khi x < 0; ngh ch bi n khi x > 0ố ồ ế ị ế
y = 0 là giá tr l n nh t c a hàm s , đt đc khi x = 0ị ớ ấ ủ ố ạ ượ
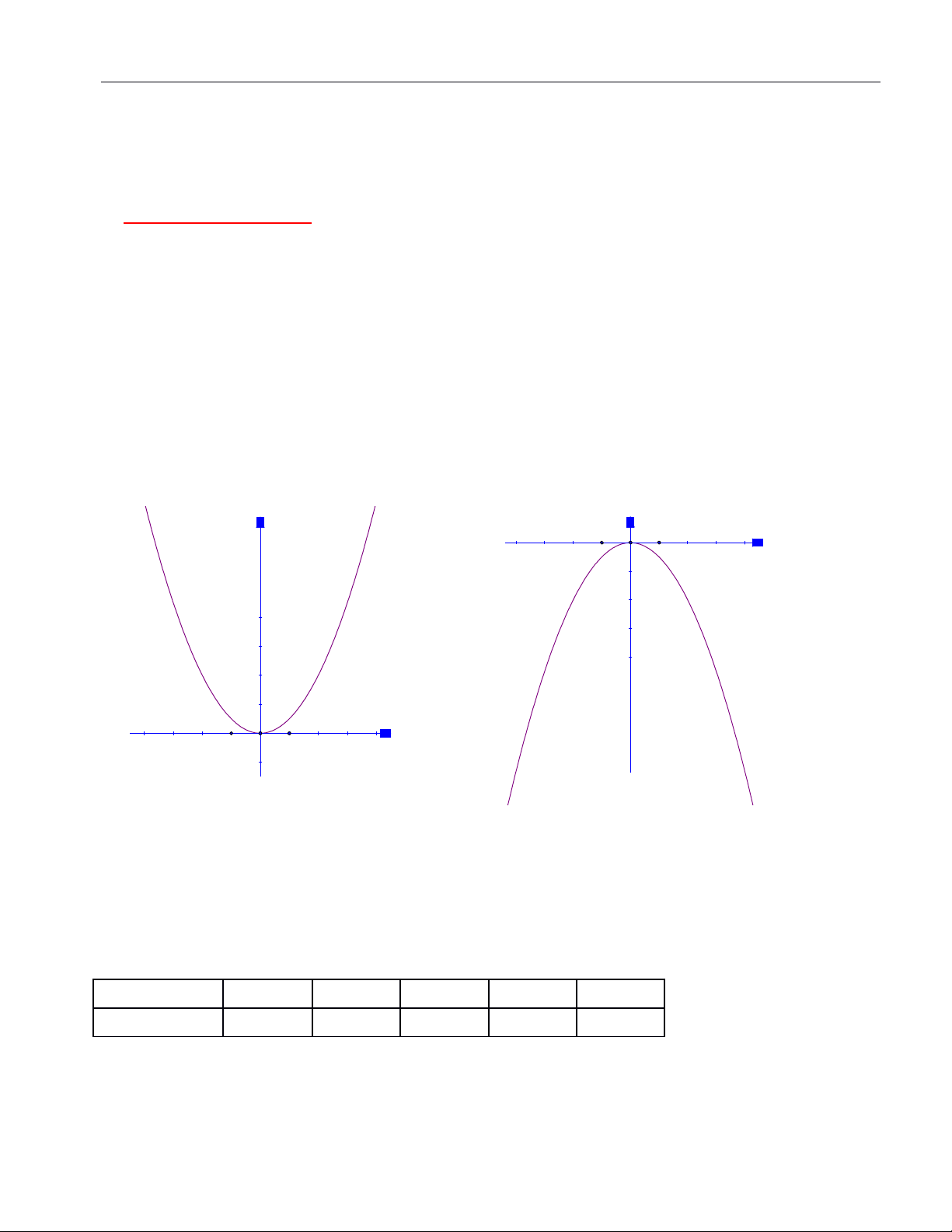
b) Đ thồ ị
Đ th hàm s y = axồ ị ố 2 (a 0) là m t parapol có đnh là góc t a đ O(0 ; 0) và nh n tr c ộ ỉ ọ ộ ậ ụ
tung làm t c đi x ng.ụ ố ứ
x
y
a > 0
y = ax
2
-1
O
1
y
a < 0
y = ax
2
-1
O
1
Là m t Parabol (P) v i đnh là g c t a đ 0 và nh n tr c Oy làm tr c đi x ng.ộ ớ ỉ ố ọ ộ ậ ụ ụ ố ứ
N u a > 0 thì đ th n m phía trên tr c hoành. 0 là đi m th p nh t c a đ th .ế ồ ị ằ ụ ể ấ ấ ủ ồ ị
N u a < 0 thì đ th n m phía d i tr c hoành. 0 là đi m cao nh t c a đ th .ế ồ ị ằ ướ ụ ể ấ ủ ồ ị
V đ th c a hàm s y = axẽ ồ ị ủ ố 2 (a0):
+ L p b ng các giá tr t ng ng c a (P)ậ ả ị ươ ứ ủ
x 0
y = ax2 (a 0 0
3
CHUYÊN Đ HÀM S B C HAIỀ Ố Ậ
+ D a và b ng giá tr v (P).ự ả ị ẽ
B. Ph ng trinh bâc hai môt ân:ươ
a) Đinh nghia: Ph ng trinh bâc hai môt ân la ph ng trinh co dang: trong đo la ân sô ; , , la ươ ươ
cac sô cho tr c goi la cac hê sô . ươ
b) Cách giai:
Công th c nghiêm tông quat cua ph ng trinh bâc hai: . ư ươ
: Ph ng trinh co hai nghiêm phân biêt: ,. ươ
: Ph ng trinh co nghiêm kep: ươ .
: Ph ng trinh vô nghiêm.ươ
Công th c nghiêm thu gon cua ph ng trinh bâc hai: . ư ươ
: Ph ng trinh co hai nghiêm phân biêt: ươ
.
: Ph ng trinh co nghiêm kep: ươ .
: Ph ng trinh vô nghiêm.ươ
C. Hê th c Vi-et va ng dung ư ư :
1. H th c Vi-ét:ệ ứ N u ph ng trình có hai nghi m xế ươ ệ 1 và x2 thì:
H th c Vi-ét th ng đc áp d ng đ tính nh m nghi m, xét d u nghi m hay tìm hai sệ ứ ườ ượ ụ ể ẩ ệ ấ ệ ố
khi bi t t ng và tích c a chúng d a vào các k t qu sau đây:ế ổ ủ ự ế ả
a. K t qu 1ế ả : Cho ph ng trình ươ
N u a + b + c = 0 thì ph ng trình có hai nghi m xế ươ ệ 1 = 1, x2 =
N u a b + c = 0 thì ph ng trình có hai nghi m xế ươ ệ 1 =1, x2 =
b. K t qu 2ế ả : Cho ph ng trình ươ
có v i ớ
Đi u ki nề ệ D u các nghi mấ ệ Mô tả
P < 0 hay a.c < 0 x1 < 0 < x2Ph ng trình có hai nghi m trái d uươ ệ ấ
P > 0, S > 0 0 < x1 x2Ph ng trình có hai nghi m d ngươ ệ ươ
P > 0, S < 0 x1 x2 < 0 Ph ng trình có hai nghi m âmươ ệ
c. K t qu 3:ế ả N u hai s a và b có a + b = S và a.b = P thì a và b là nghi m c a ph ngế ố ệ ủ ươ
trình: (Đi u ki n đ có a và b : )ề ệ ể
4
CHUYÊN Đ HÀM S B C HAIỀ Ố Ậ
D. CÁC D NG BÀI T P C B NẠ Ậ Ơ Ả
D ng 1.ạ Kh o sát s bi n thiên và v đ th hàm s y = axả ự ế ẽ ồ ị ố 2 (a ≠ 0)
1. Ph ng pháp chung:ươ
Th c hi n theo các b c sau:ự ệ ướ
a) Hàm s y = axố2 (a ≠ 0) xác đnh ị
x
R.
b) Tính bi n thiên: ph thu c vào a > 0 (ho c a < 0)ế ụ ộ ặ
c) B ng giá tr : tính t a đ ít nh t 5 đi m, trong đó có t a đ c a đi m th p nh t (a > 0) ho cả ị ọ ộ ấ ể ọ ộ ủ ể ấ ấ ặ
đi m cao nh t (a < 0).ể ấ
d) V đ th và nh n xét: đ th c a hàm s y = axẽ ồ ị ậ ồ ị ủ ố 2(a ≠ 0) là m t đng cong parabol (nhộ ườ ư
ph n II).ầ
2. Các ví dụ :
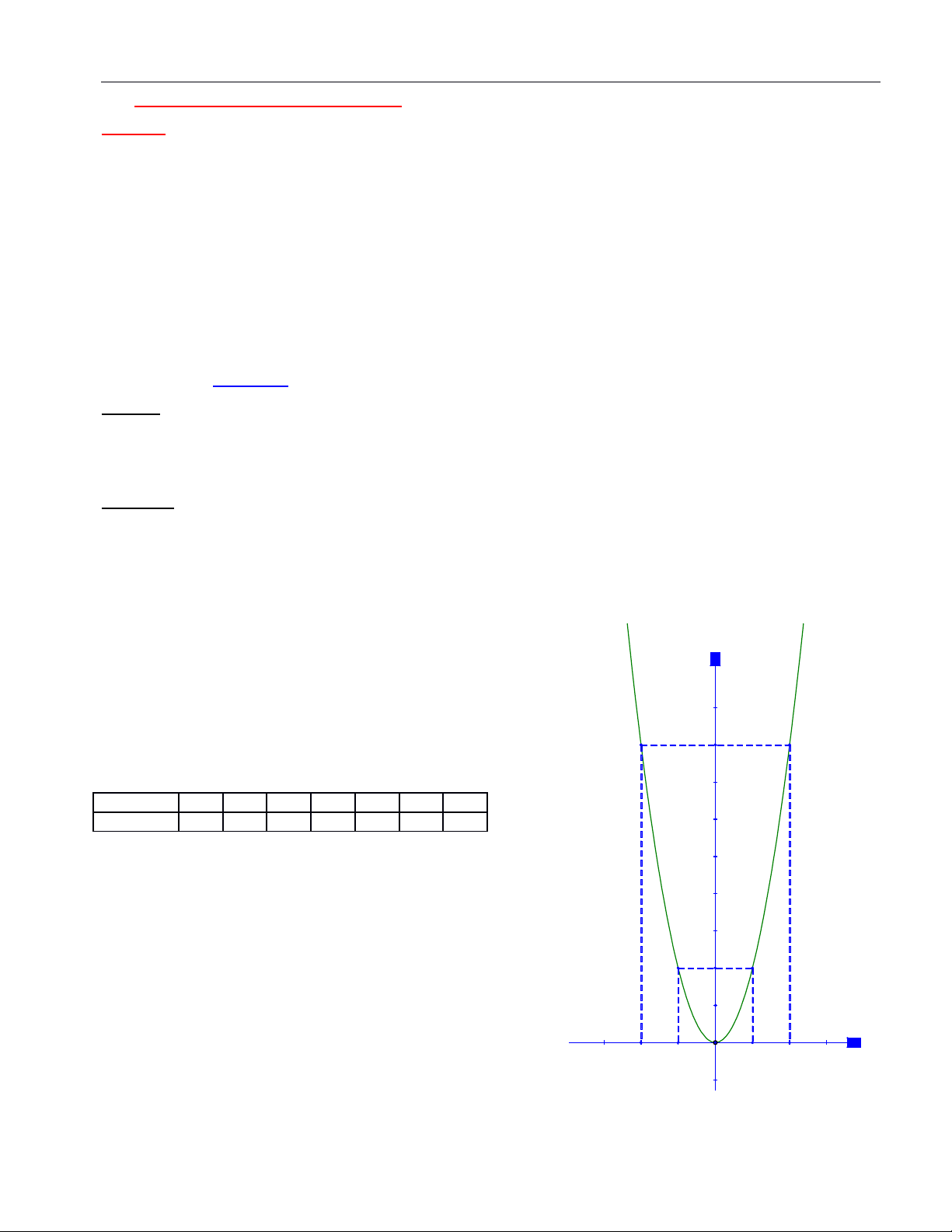
Ví d 1ụ: Xác đnh m đ đ th hàm s ị ể ồ ị ố (P)
a) Đng bi n khi x > 0 và nghich bi n khi x < 0ồ ế ế
b) Đi qua đi m . Hãy ểkh o sát s bi n thiên và ả ự ế v đ th hàm s v i m v a tìm đc.ẽ ồ ị ố ớ ừ ượ
L i gi i:ờ ả
a) Đ hàm s đng bi n khi x > 0 và ngh ch bi n khi x < 0 thìề ố ồ ế ị ế
ho c ặ
b) Đ th hàm s ồ ị ố đi qua đi m nên t a đ đi m A th a mãn ph ng trìnhể ọ ộ ể ỏ ươ
V i m = 2 ta đc: (P) y = 2xớ ượ 2
Hàm s y = 2xố2 xác đnh ị
x
R.
Tính bi n thiên: Hàm s y = 2xế ố 2 có a = 2 >0 nên hàm s :ố
+ Đng bi n khi x > 0.ồ ế
+ Ngh ch bi n khi x < 0.ị ế
B ng giá tr :ả ị
x … -2 -1 0 1 2 …
y = 2x2… 8 2 0 2 8 …
V đ th : (nh hình trên)ẽ ồ ị ư
Nh n xét: ậ
Đ th hàm s y = 2xồ ị ố 2 là m t đng cong parabol (P):ộ ườ
+ Đi qua g c t a đ.ố ọ ộ
+ Nh n tr c tung làm tr c đi x ng.ậ ụ ụ ố ứ
+ N m phía trên tr c hoành.ằ ụ
5
x
y
-1
8
-2
2
O
1