
Chuyên đề VI:
Nguyên hàm-Tích phân, ứng dụng của tích phân .
1. Tích phân
Lý huyết
-
F x
là một nguyên hàm của hàm số
y f x
liên tục trên đoạn
;
a b
. Khi đó
bb
a
a
f x dx F x F b F a
.
- Ghi nhớ các tính chất cộng, trừ tích phân và công thức tính các nguyên hàm của
hàm số thường gặp.
.
k f x dx k f x dx
, (k là hằng số)
dx x C
; 2
1dx
C
x
x
; 2
dx
x C
x
- Cách tính vi phân của hàm số
y g x
là:
d g x g x dx
Ví dụ 1: Với
3 5
u x
, ta có
3 5 3 5 .
du d x x dx
3
dx
Với 2
1
t x
, ta có 2 2
1
t x
.
Lấy vi phân hai vế (theo biến tương ứng), ta được
2 2
1
d t d x
2 2 1
t dt x dx
2 . 2 .
t dt x dx
tdt xdx
Ví dụ 2:
a)
2
2
1
3 2
I x x dx
2 2 2
2
1 1 1
3 2
x dx xdx dx
2 2 2
2
1 1 1
3 2
x dx xdx dx
2 2
3 2
2
1
1 1
3. 2
3 2
x x
x
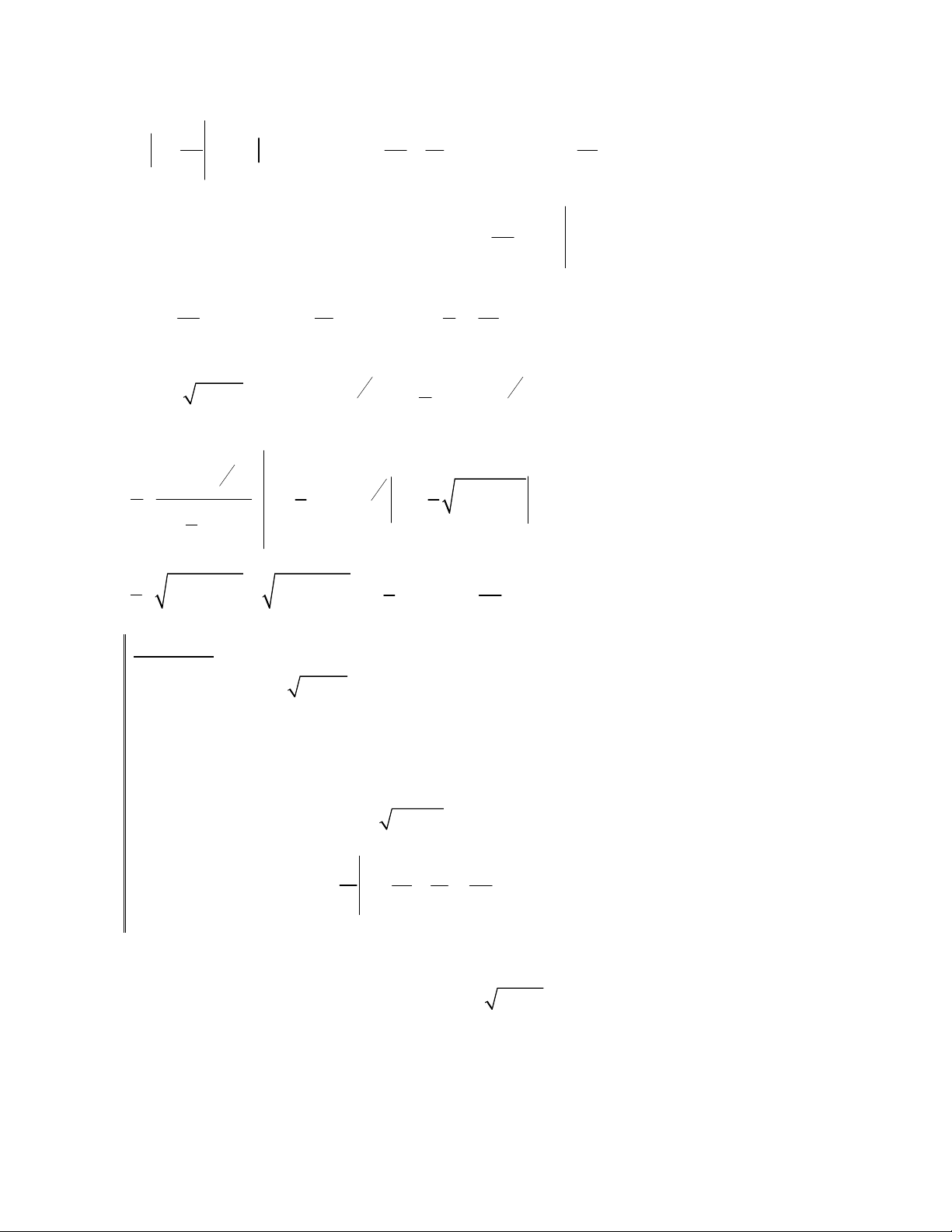
2
2
2
2
3
1
11
2
2
x
x x
2 2
3 3 2 1
2 1 2.2 2.1
2 2
15
2
Có thể tính gộp:
2
2
1
3 2
I x x dx
3
2
3
1
2
2
x
x x
2 2
3 3
2 1
2 2.2 1 2.1
2 2
5
10
2
15
2
b)
4
0
2 1
J x dx
412
0
2 1
x dx
412
0
1
2 1 2 1
2x d x
4
11
2
0
2 1
1
1
21
2
x
4
3
2
0
12 1
3x
4
3
0
1
2 1
3x
3 3
1
2.4 1 2.0 1
3
1 26
27 1
3 3
Nhận xét: Với đa số học sinh trung bình thì nên tính tích phân trên bằng phương
pháp đổi biến
2 1
t x
2
2 1
t x
Lấy vi phân hai vế (theo biến tương ứng) ta được
2
2 1 2 2
d t d x tdt dx
tdt dx
Đổi cận: Với
1
x
ta có
2.0 1 1
t
; với
4
x
ta có
3
t
Vậy
3
3 3 3
2
1 1 1
.3
t
J t tdt t dt
3 3
3 1 26
3 3 3
Bài tập:
Câu 1 (Đề TN 2008, L2, KPB): Tính
1
0
3 1
I x dx
.
Câu 2 (Đề TN 2008, L2, Ban KHXH):

Tính tích phân
2
2
1
6 4 1
I x x dx
Đáp số: Câu 1:
14
9
I; Câu 2:
9
I
2. PP đổi biến số.
Lý huyết
Một số dạng thường gặp:
1sin cos
b
a
I f x xdx
. Đặt
sin
t x
, ta có cos
dt xdx
1cos sin
b
a
I f x xdx
. Đặt
cos
t x
, ta có sin
dt xdx
Khi đó
sin
1
sin
b
a
I f t dt
hoặc
cos
1
cos
b
a
I f t dt
2
2
tan .
cos
b
a
dx
I f x
x
. Đặt
tan
t x
, ta có 2
1
cos
dt dx
x
Khi đó
tan
2
tan
b
a
I f t dt
3
b
x x
a
I f e e dx
. Đặt
x
t e
, ta có x
dt e dx
Khi đó
3
b
a
e
e
I f t dt
Tổng quát:
3.
b
a
I f u x u x dx
. Đặt
t u x
,
dt u x dx

Ví dụ 1: Tính
6
3
cos 1 sin
I x xdx
Đặt
cos
t x
, ta có
cos sin
dt d x xdx
.
Đổi cận: Với
6
x
, ta có
3
cos
6 2
t
Với
3
x
, ta có
1
cos
3 2
t
.
Khi đó
3
12 2
1
32
2
1 1
I t dt t dt
3
2
2
1
2
2
tt
22
31
2
3 1
2
2 2 2 2
3 3 1 1 3 1
8 2 8 2 2 4
Ghi chú: các em cũng có thể đặt
cos 1
t x
Ví dụ 2: Tính 2
0
cos
3 sin
x
J dx
x
Ta viết lại 2
0
1.cos
3 sin
J xdx
x
(có dạng
1
I
)
Đặt
sin
t x
, ta có
sin sin . cos
dt d x x dx xdx
Đổi cận: Với
0
x
, ta có
sin 0 0
t
.
Với
2
x
ta có
sin 1
2
t
.
Vậy
1 1
0 0
3
1
3 3
d t
J dt
t t
1
0
ln 3t
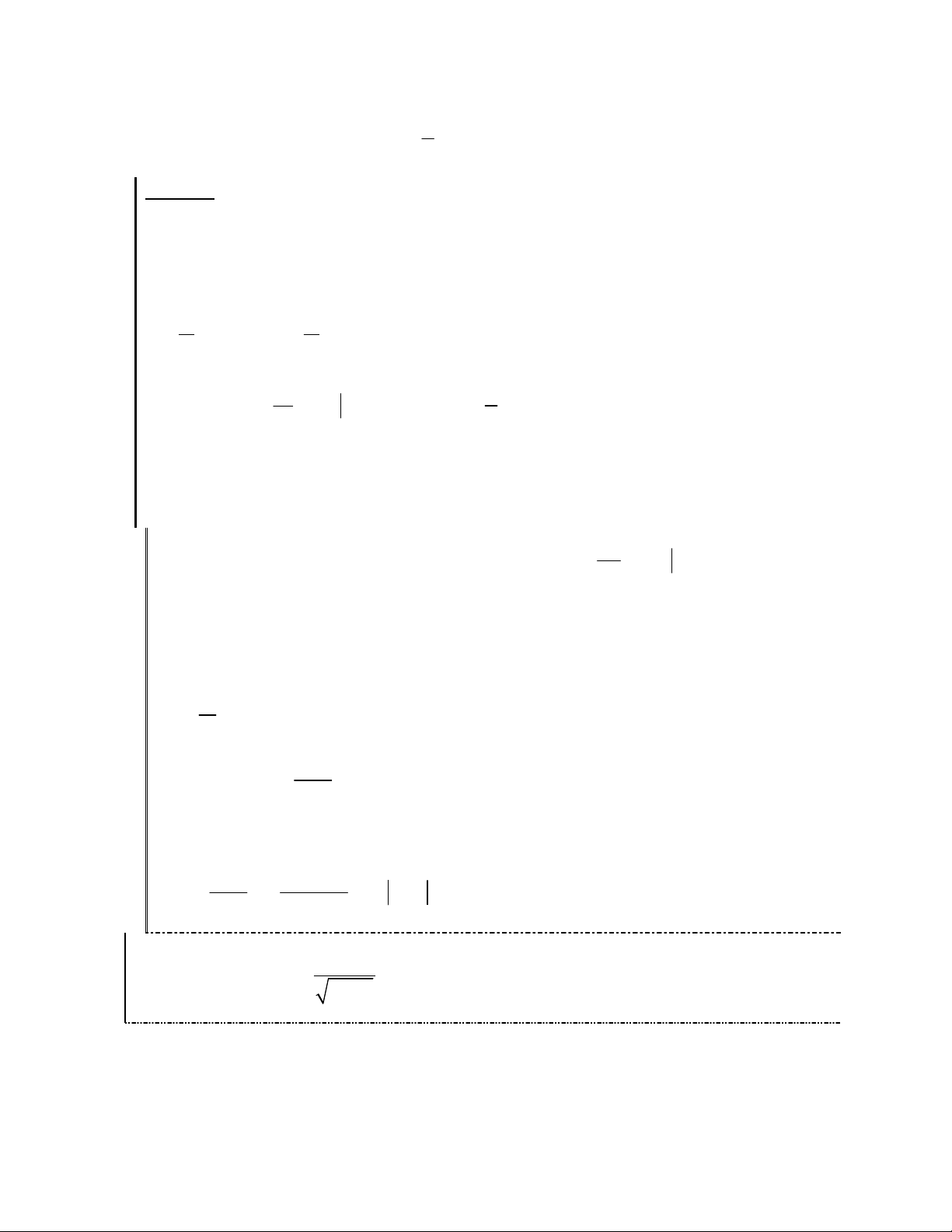
ln 1 3 ln 0 3
4
ln 4 ln 3 ln
3
Ghi chú: Với bài này có thể đặt
3 sin
t x
.
Ta có
3 sin 3 sin cos
dt d x x dx xdx
Đổi cận:
0 3 sin 0 3
x t
3 sin 3 1 4
2 2
x t
Khi đó
4
3
dt
J
t
4
3
4
ln ln 4 ln 3 ln
3
t
Cách đặt này giúp lời giải gọn và phép tính tích phân dễ thực hiện hơn rất
nhiều so với cách 1. Các em lưu ý nhé !
Ghi nhớ: Trong quá trình tính tích phân dạng
ln
b
b
a
a
du
u
u
cần vận dụng vi
phân để tính nhanh.
Chẳng hạn
dx d x m
với mọi m là hằng số.
1
dx d mx n
m
với mọi m, n là hằng số.
Ví như, trong
1
dx
x
mẫu có dạng
1
u x
, nhưng tử chưa phải du do đó cần
biến đổi để tử thành du: thay
1
dx d x
.
Vậy
1ln 1
1 1
d x
dx
x C
x x
Ví dụ 3: Tính
ln 3
0
1
x
x
e
L dx
e
Giải:
Đặt
1
x
t e
1
x x
dt e dx e dx


























