
Chuyên đề V:
Phương pháp toạ độ trong trong không gian.
1. Tọa độ của điểm, vectơ.
Lý huyết
Yêu cầu nắm được:
- Tính độ dài vecto
; ;
u a b c
:
2 2 2
u a b c
- Cho
; ;
A A A
A x y z
,
; ;
B B B
B x y z
,
; ;
C C C
C x y z
Tính tọa độ trung điểm I của đoạn AB, và trọng tâm G của tam giác ABC.
2
2
2
A B
I
A B
I
A B
I
x x
x
y y
I y
z z
z
;
3
3
3
A B C
G
ABC
G
ABC
G
x x x
x
yyy
G y
zzz
z
- Tính tọa độ vecto
AB
:
; ;
B A B A B A
AB x x y y z z
- Độ dài đoạn AB:
2 2 2
B A B A B A
AB AB x x y y z z
- Tính tích có hướng của 2 vecto
; ;
u a b c
,
; ;
v a b c
, ; ;
b c c a a b
u v
b c c a a b
, ; '
u v bc b c ca c a ab a b
- Tính tích vô hướng của 2 vecto
; ;
u a b c
,
; ;
v a b c
. . .
u v aa b b c c
- Tính góc giữa hai vecto
; ;
u a b c
,
; ;
v a b c
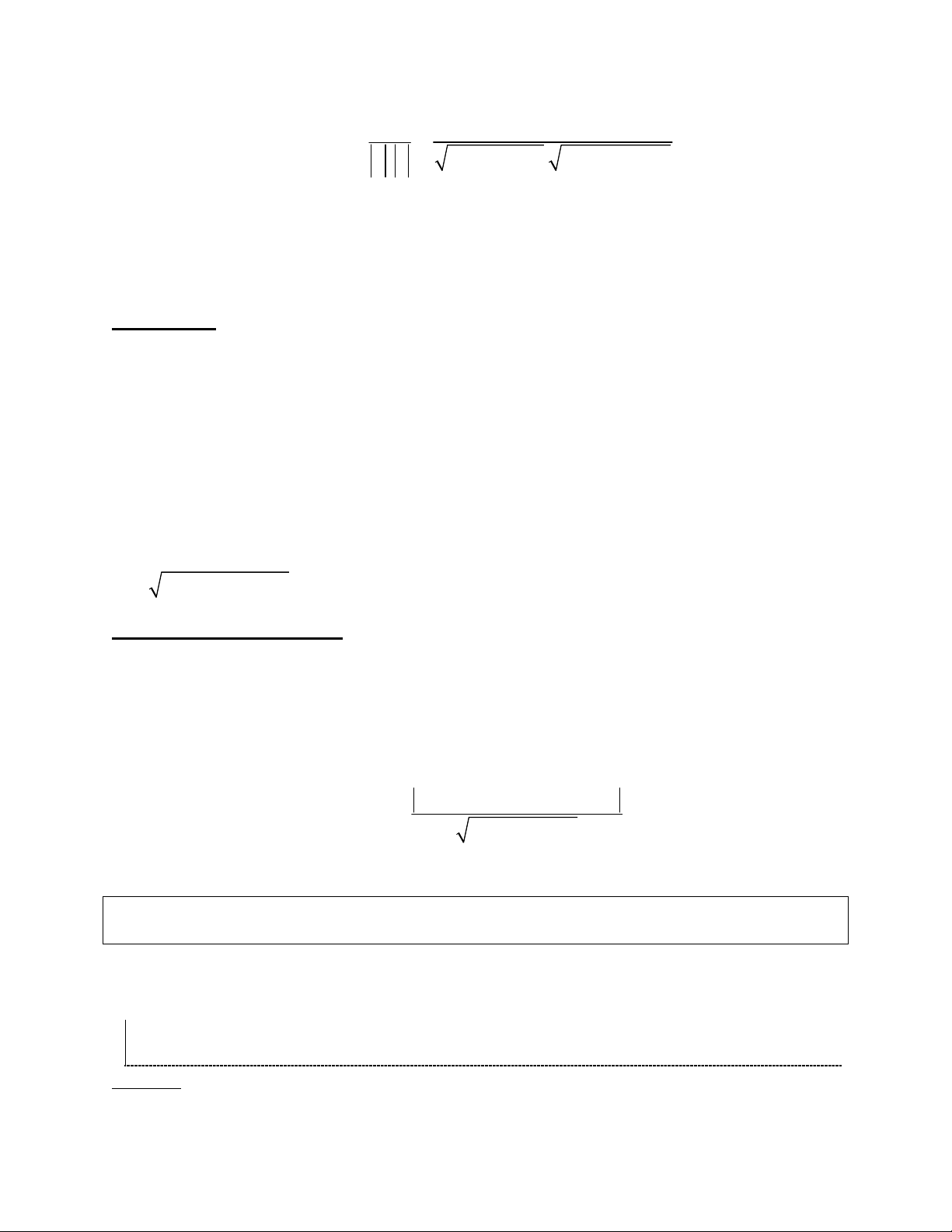
.
cos ,
.
u v
u v
u v
2 2 2 2 2 2
.
aa bb cc
a b c a b c
- Nắm được: Cách tính tọa độ điểm, tọa độ vecto thỏa mãn môt hệ thức vecto.
Ví dụ:
2. Mặt cầu.
Lý huyết
Mặt cầu tâm
; ;
I a b c
và bán kính
R
có ph/trình
2 2 2
2
x a y b z c R
Dạng thứ hai: 2 2 2
2 2 2 0
x y z ax by cz d
(2)
Với đ/kiện 2 2 2
0
a b c d
, thì (2) là p/trình mặt cầu tâm
; ;
I a b c
, bán kính
2 2 2
R a b c d
.
Một số dạng thường gặp: Mặt cầu có tâm
; ;
I a b c
và đi qua một điểm hoặc tiếp
xúc với một mặt phẳng; mặt cầu đí qua 4 điểm không đồng phẳng.
Chú ý: Khoảng cách từ điểm
; ;
M M M
M x y z
đến đường thẳng
: 0
Ax By Cz D
được tính theo công thức
;2 2 2
. . .
M M M
M
A x B y C z D
dA B C
Dạng 1: Mặt cầu đi qua một điểm M và có tâm cho trước
; ;
I a b c
Cách giải:
- Bán kính mặt cầu là
R MI
Ví dụ 1: Viết phương trình mặt cầu tâm
1;2; 3
A
và đi qua điểm
0;2;2
M.
Lời giải:
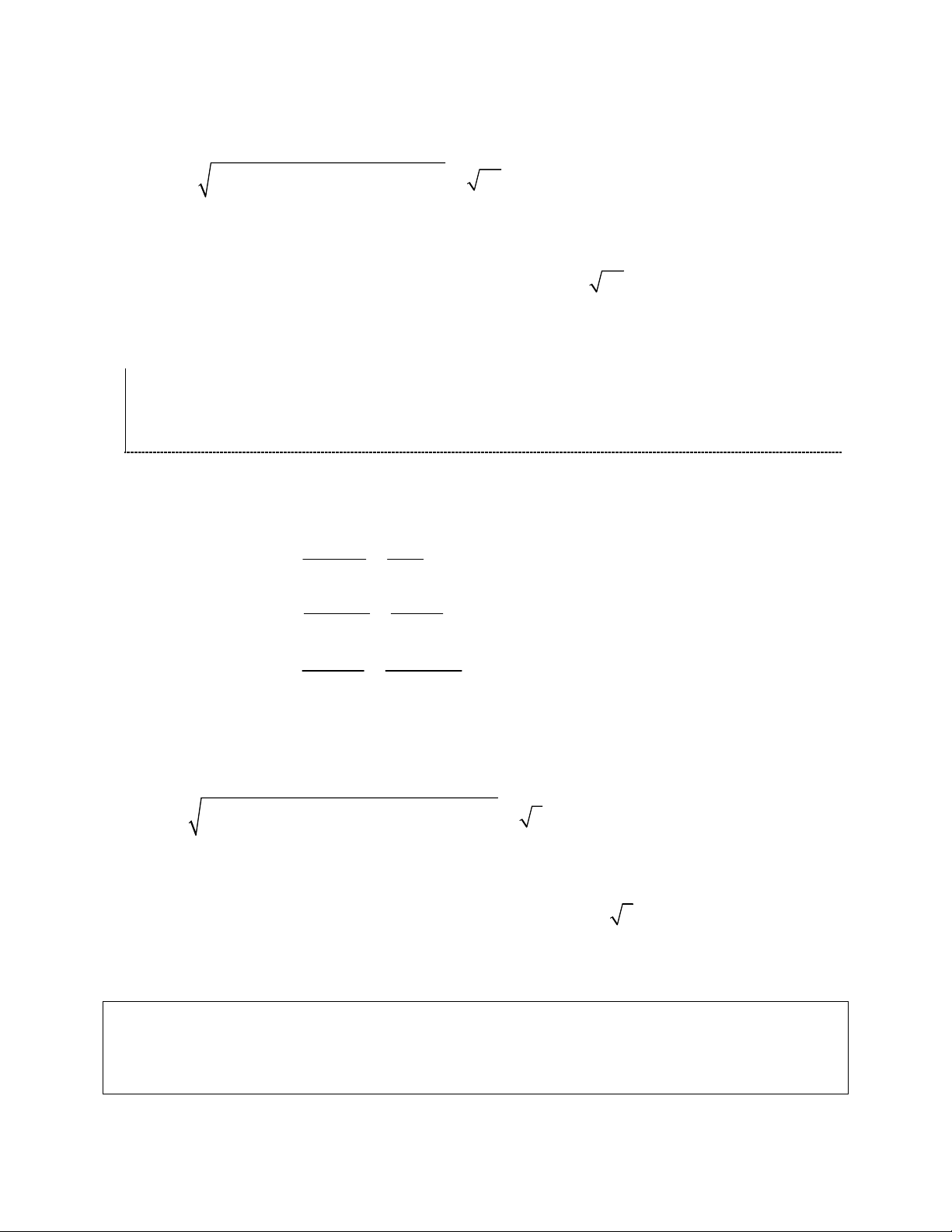
Mặt cầu đi qua điểm
0;2;2
M nên có bán kính bằng
2 2 2
1 0 2 2 3 2 26
R MA
P/trình mặt cầu (tâm
1;2; 3
A
):
2
2
2 2
1 2 3 26
x y z
Hay
2 2 2
1 2 3 26
x y z
Ví dụ 2: Viết phương trình mặt cầu đường kính AB biết
1; 2; 1
A
và
3;0; 3
B
.
Giải:
Mặt cầu đường kính AB có tâm là trung điểm I của đoạn AB.
Tọa độ tâm I là
1 3 2
2 2
2 0
1
2 2
1 3
2
2 2
A B
I
A B
I
A B
I
x x
x
y y
y
z z
z
Hay
2; 1; 2
i
Bán kính mặt cầu
2 2
2
1 2 2 1 1 2 3
R IA
P/trình mặt cầu cần tìm:
2
2 2
2
2 1 2 3
x y z
Hay
2 2 2
2 1 2 3
x y z
Dạng 2: Mặt cầu có tâm
; ;
I a b c
và tiếp xúc với mặt phẳng
: 0
P Ax By Cz D
.
Cách giải:

- Bán kính mặt cầu bằng khoảng cách từ tâm I đến mp
P
.
Ví dụ 3: Viết ph/trình mặt cầu có tâm
0; 1;1
M và tiếp xúc với mặt phẳng
: 2 1 0
P x y z
.
Lời giải:
Mặt cầu tiếp xúc với mp
P
nên bán kính m/cầu bằng khoảng cách từ tâm M đến
mp
P
:
,
2
2 2
0 1 2.1 1
1 1 2
M P
R d
2
2
6 6
P/trình mặt cầu cần tìm (tâm
0; 1;1
M):
2
2
2 2
2
0 1 1
6
x y z
Hay
2 2
2
2
1 1
3
x y z
Bài tập:
Câu 1 (Đề TN 2007, L2, Ban KHTN): Trong không gian với hệ toạ độ Oxyz, cho
hai điểm E(1;-4;5) và F(3;2;7).
1. Viết phương trình mặt cầu đi qua điểm F và có tâm là E.
2. Viết phương trình mặt phẳng trung trực của đoạn thẳng EF .
3. Phương trình mặt phẳng.
Lý huyết
Dạng 1: Mặt phẳng đi qua điểm
;
M M M
M x y z
và có vecto pháp tuyến
; ;
n A B C
.
PTTQ của mp là
0
M M M
A x x B y y C z z
Một số dấu hiệu:

- Mặt phẳng
P
vuông góc với đường thẳng AB¸ hoặc đường thẳng
d
. Khi đó
vecto
AB
hoặc vecto chỉ phương
d
u
của
d
là vecto pháp tuyến của mp
P
.
- Mặt phẳng
P
song song với mặt phẳng
Q
, khi đó vecto pháp tuyến
Q
n
của
mp
Q
cũng là vecto pháp tuyến của mp
P
.
Ví dụ 1: Viết phương trình tổng quát của mặt phẳng
P
đi qua điểm
1;2; 3
A
và :
a) vuông góc với đường thẳng
1 2
:
2 1 3
x y z
d
b) song song với mặt phẳng
: 3 0
Q x y z
c) vuông góc với đường thẳng AB với
0;1;1
A,
1;2;0
B
Lời giải:
a) Đ/thẳng
d
có vecto chỉ phương
2; 1;3
u
.
P d
nên
P
nhận
2; 1;3
u
làm vecto pháp tuyến.
Mặt khác
P
đi qua điểm
1;2; 3
A
.
Vậy p/trình tổng quát của
P
:
2 1 1 2 3 3 0
x y z
Hay
2 3 9 0
x y z
b)
||
P Q
nên vecto pháp tuyến của
Q
,
1; 1; 3
n
cũng là vecto pháp
tuyến của
P
.
Mặt khác
P
đi qua điểm
1;2; 3
A
.
Vậy p/trình tổng quát của
P
:
1 1 1 2 3 3 0
x y z
Hay
3 8 0
x y z


























