Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
133
DAO ĐỘNG TỰ DO CỦA DẦM CÓ CƠ TÍNH BIẾN THIÊN
TRONG MÔI TRƯỜNG NHIỆT ĐỘ CAO
Bùi Văn Tuyển1, Trần Thị Thơm2, Nguyễn Đình Kiên2
Đại học Thủy lợi, email: tuyenbv@tlu.edu.vn
2Viện Cơ học - Viện Hàn lâm Khoa học Việt Nam, email: ndkien@imech.ac.vn
1. GIỚI THIỆU
Vật liệu có cơ tính biến thiên (FGM)
phát minh năm 1984, là một loại composit
mới tạo từ hai hay nhiều loại vật liệu thành
phần, thường là gốm và kim loại với sự
phân bố tỷ lệ thể tích của các vật liệu thành
phần liên tục theo một hoặc vài hướng.
Trong bài báo này chúng tôi tập trung vào
nghiên cứu dao động tự do của dầm FGM
trong môi trường nhiệt độ cao bằng phương
pháp phần tử hữu hạn. Dầm được tổ hợp từ hai
vật liệu thành phần là gốm và kim loại với các
tính chất của vật liệu phụ thuộc vào nhiệt độ.
Sự phân bố của nhiệt độ theo chiều cao dầm
nhận được từ lời giải phương trình truyền nhiệt
Fourier. Phần tử được lựa chọn cho nghiên cứu
này là phần tử dầm Euler-Bernoulli hai nút.
Kết quả của nghiên cứu đã làm nổi bật ảnh
hưởng của nhiệt độ cũng như tham số của vật
liệu tới tần số dao động riêng của dầm.
2. XÂY DỰNG CÔNG THỨC
2.1. Phương trình cơ bản
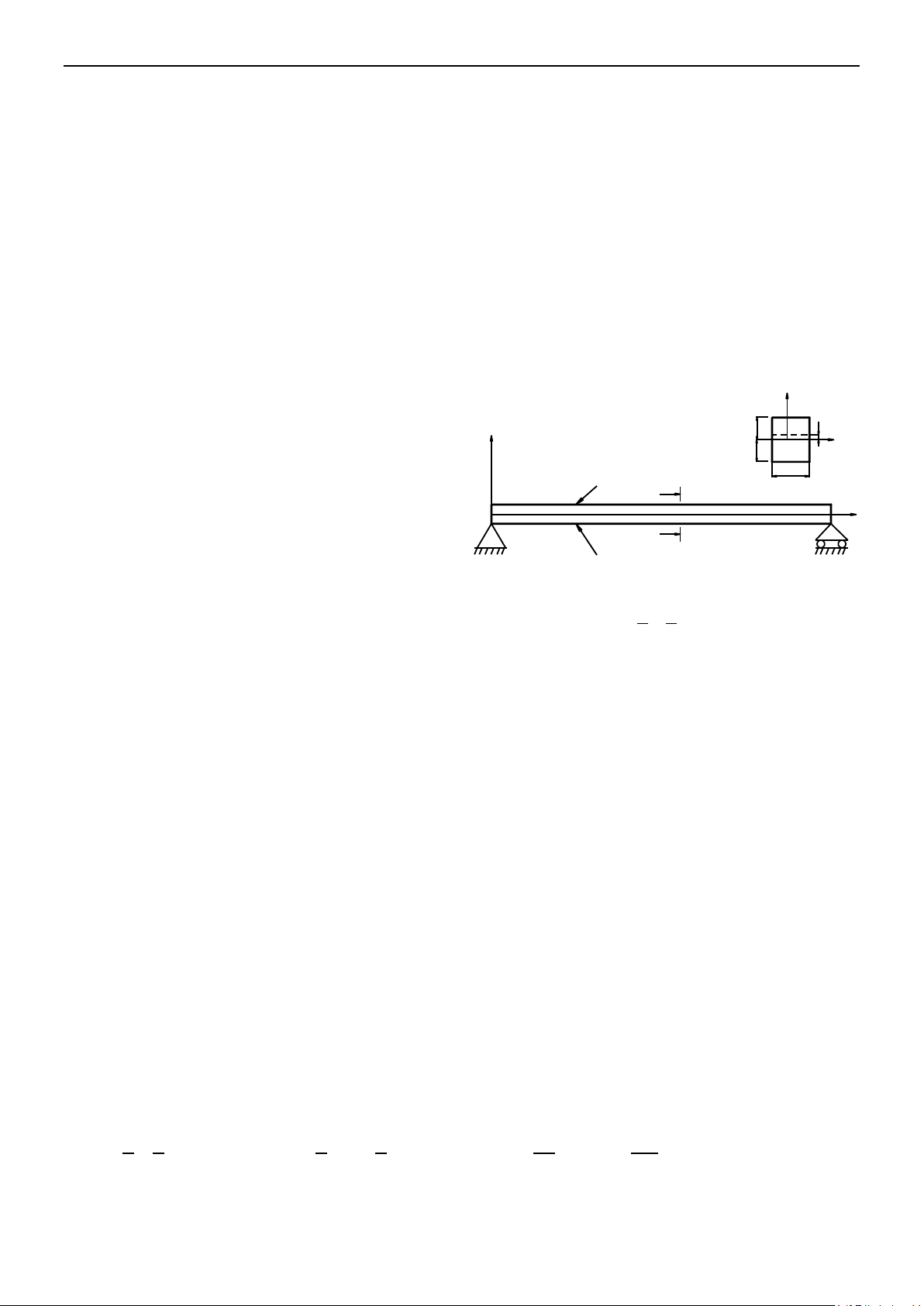
Xét dầm FGM tựa giản đơn với chiều dài
L, chiều cao h, chiều rộng b trong hệ trục tọa
độ (xoz) như minh họa trên Hình 1. Trục x
nằm trong mặt giữa dầm, trục z vuông góc
với mặt giữa. Tỷ lệ thể tích của gốm (Vc) và
kim loại (Vm) được giả định tuân theo quy
luật hàm số mũ:



n
c c m
z 1 h h
V , V V 1, z
h 2 2 2
(1)
Tính chất hữu hiệu P(z) được đánh giá
theo mô hình Voigt có dạng:
h/2
h0
x
z
y
b
0
h/2
z w
A
A
Section A-A
ceramic
metal
Hình 1: Dầm FGM trong môi trường nhiệt độ

1
( ) ( ) 2
n
c m m
z
P z P P P
h



(2)
Trong đó: n là tham số vật liệu, xác định
sự phân bố của các thành phần vật liệu; chỉ số
‘c’ và ‘m’ dùng để chỉ pha gốm và pha kim
loại. Pc, Pm tương ứng là tính chất của gốm
và kim loại (môđun Young E, hệ số Poisson
v, hệ số truyền nhiệt K…), phụ thuộc vào
nhiệt độ:
1 2 3
0 1 1 2 3
1P P P T PT PT PT
(3)
Trong đó T=T0+ΔT(z) với T0=300oK là
nhiệt độ phòng, P0, P-1, P1, P2 and P3 là các
hệ số nhiệt ứng với các loại vật liệu khác
nhau, ΔT(z) là lượng tăng nhiệt độ.
Theo lý thuyết dầm Euler-Bernoulli,
chuyển vị của một điểm bất kỳ trên dầm theo
phương x và z là u1 và u3 cho bởi:
1 0 ,
3
( , , ) ( , ) ( , )
( , , ) ( , )
x
u x z t u x t z h w x t
u x z t w x t
(4)
Giải phương trình truyền nhiệt Fourier:
( , ) 0
d dT
zT
dz dz




(5)
Ta nhận được trường nhiệt độ T phụ thuộc
vào biến z, nhiệt độ mặt gốm Tc và mặt kim
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
134
loại Tm dưới dạng (eq.6). Với T=Tm(z=-h/2)
và T=Tc (z=h/2).
(6)
Tổng năng lượng biến dạng của dầm:

pt
U U U
(7)
Trong đó Up là năng lượng biến dạng đàn
hồi của dầm, có dạng:



L22
p 11 ,x 22 ,xx
0
1
U A u A w dx
2
(8)
Ut là năng lượng biến dạng do sự tăng
nhiệt độ xác định theo (Wattanasakulpong et
al., 2011)
2 2 2
, , ,
00
11
( w )
22
LL
t T x x T x
U N u dx M dx

(9)
Trong công thức (8) và (9):

2
11 22 0
A
( A ,A ) E z,T 1, z h dA
(10)

TA
N E z,T ( z,T ) TdA

(11)
2
TA
M E z,T ( z,T ) Tz dA

(12)
Động năng của dầm là:
2 2 2
11 12 , 22 ,
0
1w
2
L
xx
T I u I uw I w dx


(13)
Trong đó
2
11 12 22 0 0
, , , 1, ,
A
I I I z T z h z h dA
(14)
Áp dụng nguyên lý Hamilton, ta nhận
được phương trình vi phân chuyển động:
11 12 ,x 11 ,xx
11 12 ,x 22 ,x 22 ,xxxx
I u I w A u 0
I w I u I w A w 0
(15)
2.2. Công thức phần tử hữu hạn
Để giải phương trình (15) ta dùng phương
pháp phần tử hữu hạn. Giả sử dầm được chia
thành một số phần tử hai nút có chiều dài là l.
Véc tơ chuyển vị nút của một phần tử là:
T
i i i j j j
u w u w

d
(16)
Chuyển vị dọc trục u và chuyển vị ngang
w được biểu diễn qua chuyển vị nút là:

TT
uw
uwN d N d,
(17)
Trong đó Nu và Nw tương ứng là các ma trận
hàm dạng của u và w. Thay Phương trình
(17) vào các phương trình (8), (9), (13) ta có
thể biểu diễn các biểu thức năng lượng dưới
dạng sau đây:
11
w
11
w
11
11
22
11
()
22
11 )
22
el el
el el
el el
nn
p p uu
ii
nn
T T T
t T uu w
ii
nn
uu w u
ii
U
U
T










d k d d k k d
d k d d k k k d
d md d m m m m d
TT
TT
TT
+
=(
(18)
Trong phương trình (18), kuu, kθθ lần lượt
là ma trận độ cứng dọc trục và ma trận độ
cứng chống uốn;
w
,,
T T T
uu w

k k k
lần lượt là ma
trận độ cứng sinh ra từ việc tăng nhiệt độ;
w
, , ,
wu
uu
m m m m
lần lượt là ma trận
khối lượng nhất quán sinh ra từ chuyển dịch
dọc trục; chuyển vị ngang; tương tác giữa
chuyển vị dọc trục và quay của thiết diện
ngang, và sự quay của thiết diện ngang. Ma
trận độ cứng và ma trận khối lượng nhất quán
tổng thể của dầm K, M có được từ việc ghép
nối các ma trận phần tử.
Phương trình chuyển động tự do của dầm
0MD KD
(19)
3. KẾT QUẢ VÀ THẢO LUẬN
Xét dầm tựa giản đơn được tổ hợp từ hai
vật liệu thành phần là thép không gỉ
(SUS304) và nhôm ôxit (Al203). Các hệ số
phụ thuộc vào nhiệt độ của SUS304 và Al203
được lấy từ (Mahi; 2010).
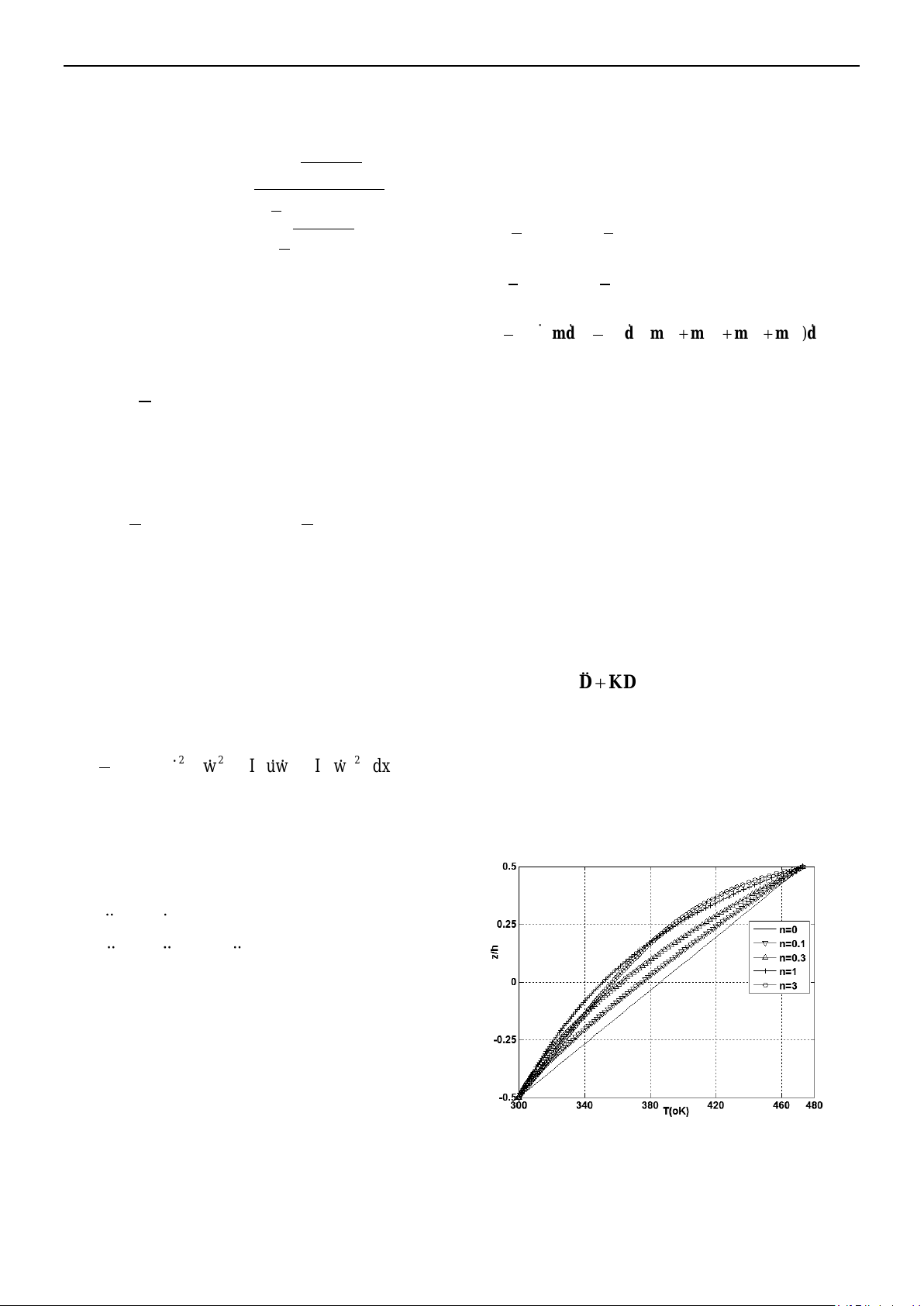
Hình 2: Sự phân bố nhiệt độ theo chiều cao dầm
Hình 2 thể hiện sự phân bố nhiệt độ theo
chiều cao của dầm. Nhiệt độ mặt trên của
dầm là 473oK và mặt dưới của dầm là 300oK.
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
135
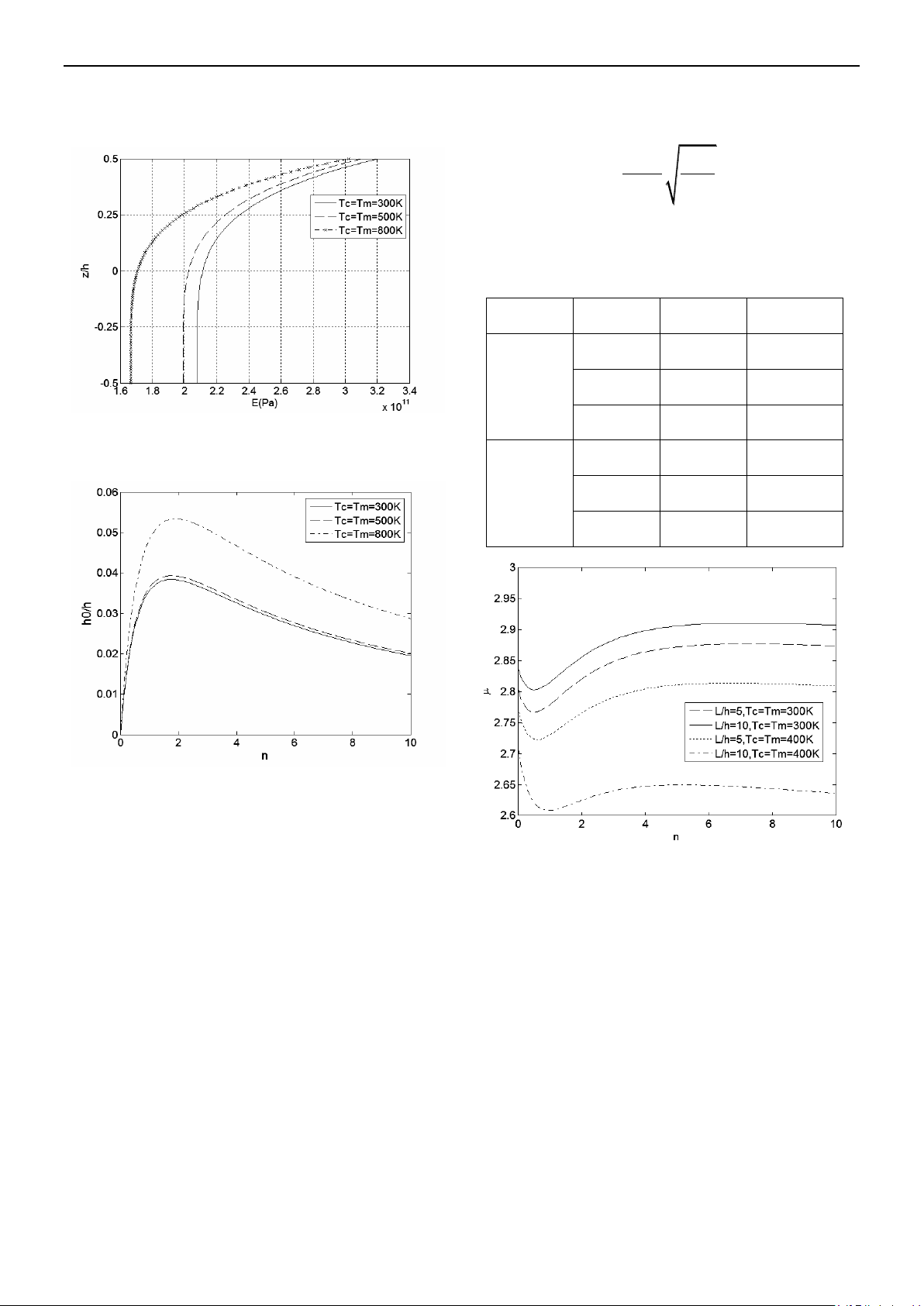
Hình 3 khi nhiệt độ tăng modun đàn hồi
giảm và giảm nhanh khi nhiệt độ tăng cao.
Hình 3: Ảnh hưởng của nhiệt độ tới modun
đàn hồi E theo chiều cao của dầm với n=5
Hình 4: Ảnh hưởng của tham số n tới h0/h
Hình 4 minh họa ảnh hưởng của tham
số vật liệu n tới vị trí mặt trung hòa với các
giá trị khác nhau của nhiệt độ. Khi nhiệt độ
tăng thì tỷ số h0/h tăng với bất kể giá trị
nào của n. Nói cách khác, khi tăng nhiệt độ
thì vị trí trục trung hòa sẽ dịch chuyển về
phía pha gốm.
Theo sự hiểu biết của tác giả do không có
kết quả nghiên cứu nào về dao động tự do
của dầm FG trong môi trường nhiệt độ để so
sánh. Vì thế các công thức tính toán trong bài
báo này được kiểm tra trong trường hợp
T=0 (T=300oK), và sau đó so sánh với kết
quả về dao động tự do không kể đến nhiệt độ
của Simsek (2010). Kết quả liệt kê trong
bảng 1 tính với dầm làm từ Al/Al203 cho ta
thấy kết quả của bài báo hoàn toàn phù hợp
với kết quả đã được công bố trước đó. Tham
số tần số cơ bản được định nghĩa là:
211
11
LI
hA
(20)
Bảng 1: So sánh tham số tần số cơ bản
của dầm Al/Al203 không chịu ảnh hưởng
của nhiệt độ
n
L/h
Kết quả
Simsek[1]
0.3
10
2.731
2.731
30
2.741
2.741
100
2.742
2.743
Al
10
2.837
2.837
30
2.848
2.847
100
2.849
2.848
Hình 5: Tham số tần số cơ bản
của dầm FG làm từ Al203/SUS304 với
các giá trị khác nhau của n
Hình 5 cho thấy cùng tỷ số L/h, khi tăng
nhiệt độ thì tham số tần số giảm rõ rệt với bất
kể giá trị nào của n. Giá trị của thay đổi
nhiều với n=0-5, và thay đổi ít khi n>5. Khi tỷ
số L/h tăng cùng với sự tăng của nhiệt độ thì
cũng giảm. Điều đó chứng tỏ khi (L/h) lớn thì
ảnh hưởng của nhiệt độ càng mạnh mẽ.
4. TÀI LIỆU THAM KHẢO
[1]. Şimşek, M., Vibration analysis of a functionally
graded beam under a moving mass by using
different beam theories, Composite Structures,
2010, Vol. 92 (4), p. 904-917.