ĐỀ ÔN THI ĐẠI HỌC 2009
ĐỀ SỐ 1
Môn : TOÁN Khối : A
Thời gian làm bài : 180 phút không kể thời gian phát đề
−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−−
−
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH
Câu I (2 điểm)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y =
1
52
2
+
++
x
xx
2.
D
ự
a vào
đồ
th
ị
(C), tìm m
để
ph
ươ
ng trình sau có 2 nghi
ệ
m d
ươ
ng phân bi
ệ
t:
)1)(52(52
22
+++=++ xmmxx
Câu II (2 điểm)
1.
Gi
ả
i ph
ươ
ng trình:
8
232
sin3sincos3cos
33
+
=− xxxx
2. Giải hệ phương trình:
=−++
=+++
yxyx
yxyyx
)2)(1(
4)(1
2
2
(x, y
∈
)
Câu III (2 điểm)
Trong không gian với hệ toạ độ Oxyz,cho hình lăng trụ đứng ABC.A’B’C’ có
A(0; 0; 0), B(2; 0; 0), C(0; 2; 0),A’(0; 0; 2).
1. Chứng minh A’C vuông góc với BC’ .Viết phương trình mặt phẳng (ABC’).
2. Viết phương trình hình chiếu vuông góc của đường thẳng B’C’ trên mặt phẳng (ABC’)
Câu IV (2 điểm)
1. Tính tích phân:
∫
+++
=
5
3
1412 xx
dx
I
2.
Cho x,y là các s
ố
th
ự
c th
ỏ
a mãn
đ
i
ề
u ki
ệ
n x
2
+xy+y
2
≤ 3 .Ch
ứ
ng minh r
ằ
ng
–4
3
–3 ≤ x
2
– xy – 3y
2
≤ 4
3
+3
PHẦN TỰ CHỌN: Thí sinh tự chọn câu V.a hoặc câu V.b
Câu V.a.(2 điểm)
1– Trong m
ặ
t ph
ẳ
ng v
ớ
i h
ệ
t
ọ
a
độ
Oxy , cho elip (E) 1
2
12
22
=+ yx .Vi
ế
t ph
ươ
ng trình
hypebol (H) có hai
đườ
ng ti
ệ
m c
ậ
n là y = ±2x và có 2 tiêu
đ
i
ể
m là 2 tiêu
đ
i
ể
m c
ủ
a elip (E) .
2– Áp d
ụ
ng khai tri
ể
n nh
ị
th
ứ
c Niuton c
ủ
a
(
)
100
2
xx +
, Ch
ứ
ng minh r
ằ
ng
0
2
1
.200
2
1
.199..............
2
1
.101
2
1
.100
199
100
100
198
99
100
100
1
100
99
0
100
=
+
−+
−
CCCC
(
C
k
n
là số tổ hợp chập k của n phần tử ).
Câu V.b.(2 điểm)
1. Giải bất phương trình 2)2(log
1
>
−
+
x
x
2. Cho hình hộp đứng ABCD.A’B’C’D’ có các cạnh AB=AD=a , AA’ =
2
3a và góc
BAD =60
0
. Gọi M và N lấn lượt là trung điểm của các cạnh A’D’ và A’B’. Chứng minh
rằng AC’ vuông góc với mặt phẳng (BDMN). Tính thể tích khối chóp A.BDMN.
–––––––––––––––––––––––––– Hết ––––––––––––––––––––––––––––
0
1
I
-
1
4
-
3
-
4
x
y
ĐÁP ÁN – THANG ĐIỂM
ĐỀ ÔN THI ĐẠI HỌC NĂM 2009
ĐỀ SỐ 1
Môn : TOÁN Khối : A
( Đáp án – Thang điểm gồm 5 trang )
Câu
Ý Nội dung Điểm
I 2,00
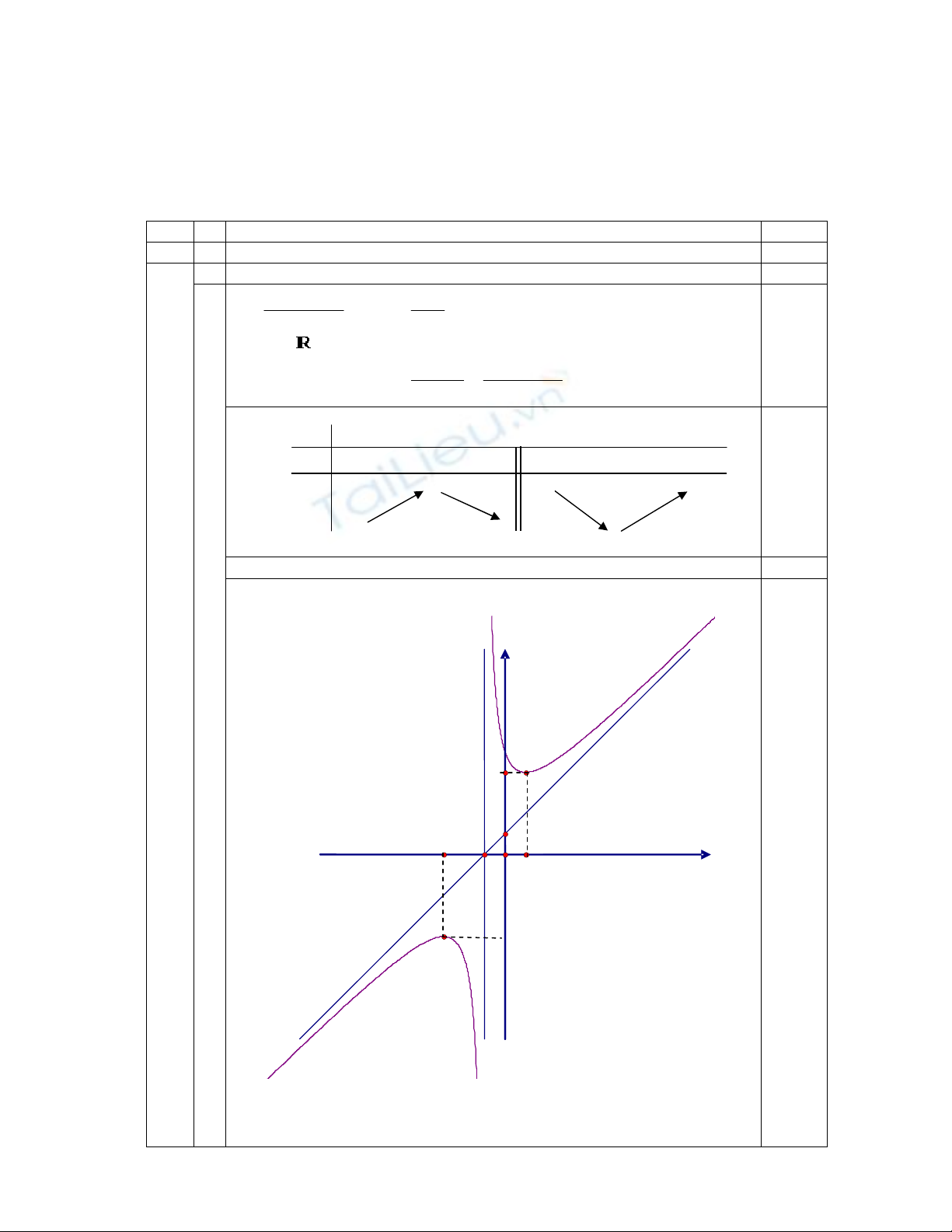
1 Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1,00 điểm)
y =
1
4
1
1
52
2
+
++=
+
++
x
x
x
xx
• TXĐ : \{–1}
• Sự biến thiên : y’ =
( ) ( )
2
2
2
1
32
1
4
1+
−+
=
+
−
x
xx
x; y’=0
⇔
x =1; x = –3
0,25
Bảng biến thiên :
x – ∞ –3 –1 1 +∞
y’ + 0 – – 0 +
–4 + ∞ +∞
– ∞ –∞ 4
Cực trị: y
CĐ
= y(–3) = –4 , y
CT
= y(1) = 4
0,50
•
Tiệm cận:Tiệm cận đứng x = –1 , Tiệm cận xiên y = x +1
•
Đồ thị :
2
T
ì
m
m đ
ể ph
ương tr
ình sau có 2 nghi
ệm d
ương phân bi
ệt
(1,00 đi
ểm).
Phương trình đã cho tương đương với :
1
52
2
+
++
x
xx =
52
2
++ mm
0,25
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
y =
1
52
2
+
++
x
xx với đường thẳng y =
52
2
++ mm
0,25
Phương trình đã cho có 2 nghiệm dương khi và chỉ khi :
4 <
52
2
++ mm
< 5
⇔
<<−
−≠
02
1
m
m
0,50
II 2,00
1 Giải phương trình (1,00 điểm)
Phương trình đã cho tương đương với :
cos3x(cos3x + 3cosx) – sin3x(3sinx – sin3x) =
2
232 +
⇔
cos
2
3x + sin
2
3x + 3(cos3xcosx – sin3xsinx) =
2
232 +
⇔
cos4x =
2
2
0,50
⇔ 4x = ±
2
16
2
4
π
π
π
π
kxk +±=⇔+ 0,50
2 Giải hệ phương trình (1,00 điểm)
Hệ đã cho tương đương với :
=−+
=
+
⇔
=−+
+
=−++
+
12
1
1
1)2(
1
22
1
2
2
2
xy
y
x
xy
y
x
xy
y
x
⇔
0,50
⇔
−=
=−+
xy
xx
3
02
2
⇔
=
=
2
1
y
xho
ặ
c
=
−=
5
2
y
x
0,50
III
2,00
1
Ch
ứ
ng minh AC’
⊥
BC’ .Vi
ế
t ph
ươ
ng trình mp(ABC’) (1,00
đ
i
ể
m)
• Ta có : C’(0;2;2) ,
→
CA' =(0;2;–2) ,
→
'BC
= (–2;2;2)
→
CA'
.→
'BC
= 0.(–2)+2.2+(–2).2 = 0 ⇒ A’C ⊥ BC’
0,50
•
Vì A’C
⊥
BC’ , A’C
⊥
AB nên A’C
⊥
(ABC’)
Vectơ pháp tuyến của mặt phẳng (ABC’) là
→
n=
→
AC =(0;2;–2)
Phương trình mặt phẳng (ABC’) là :
0.(x–0) + 2(y–0) –2(z–0) = 0
⇔
y – z = 0.
0,50
2
(1,00
đ
i
ể
m)
Ta có
→
''CB =
→
BC =(–2;2;0). Gọi (
α
) là mặt phẳng chứa B’C’ và vuông
góc với mặt phẳng (ABC’) thì hình chiếu vuông góc của B’C’ trên (ABC’)
là giao tuyến của (
α
) và (ABC’)
0,25
Vectơ pháp tuyến của (
α
) là
→
α
n
=[
→
''CB ;
→
n
] = (–4;–4;–4)
0,25
Ph
ươ
ng trình c
ủ
a (
α
): 1(x–0)+1.(y–2)+1.(z–2) = 0
⇔
x + y + z – 4 = 0
0,25
Ph
ươ
ng trình hình chi
ế
u c
ủ
a B’C’ trên (ABC’) là :
=−
=−++
0
04
zy
zyx
0,25
IV
2,00
1
Tính tích phân (1,00
đ
i
ể
m)
Đặ
t t =
14 +
x
⇒
x = tdtdx
t
2
1
4
1
2
=⇒
−
0,25
Ta có
( ) ( )
∫∫
+
−
+
=
+
5
32
5
32
1
1
1
1
1dt
t
t
t
tdt
0,50
= 12
1
2
3
ln
1
1
)1ln(
5
3
−=
+
++ t
t
0,25
2
Ch
ứ
ng minh: – 4
3
–3 ≤ x
2
– xy – 3y
2
≤ 4
3
–3 (1,00
đ
i
ể
m)
Đặ
t A =
2
x
+ xy +
2
y
,B ==
2
x
– xy –3
2
y
N
ế
u y = 0 thì B=
2
x
⇒ 0 ≤ B ≤ 3
0,25
N
ế
u y ≠0 thì
đặ
t t =
y
x
ta
đượ
c B = A. 1
3
.
3
2
2
22
22
++
−−
=
++
−−
tt
tt
A
yxyx
yxyx
0,25
Xét ph
ươ
ng trình
m
t
t
tt
=
+
+
−−
1
3
2
2
⇔ (m–1)t
2
+ (m+1)t + m + 3 = 0 (1)
Ph
ươ
ng trình (1) có nghi
ệ
m khi và ch
ỉ
khi m = 1 ho
ặ
c
∆ = (m+1)
2
– 4(m–1)(m+3) ≥ 0 ⇔
3
483 −−
≤ m ≤
3
483 +−
Vì 0 ≤ A ≤ 3 nên –3– 34 ≤ B ≤ –3+ 34
0,50
V.a
2,00
1
(1,00
đ
i
ể
m)
(E): 1
2
12
22
=+
yx
có hai tiêu
đ
i
ể
m là F
1
(–
10
;0) , F
2
(
10
;0)
Vì (H) có cùng tiêu
đ
i
ể
m v
ớ
i (E) nên ph
ươ
ng trình c
ủ
a (H) có d
ạ
ng:
1
2
2
2
2
=−
b
y
a
x
0,25
Vì (H) có cùng tiêu
đ
i
ể
m v
ớ
i (E) nên
a
2
+ b
2
= c
2
= 10 (1)
0,25
Vì (H) có hai
đườ
ng ti
ệ
m c
ậ
n là y =
±
2x nên b = 2a (2) 0,25
T
ừ
(1) và (2) suy ra a
2
= 2 , b
2
= 8
Ph
ươ
ng trình c
ủ
a (H) là : 1
8
2
22
=−
yx
0,25
2
Áp d
ụ
ng khai tri
ể
n nh
ị
th
ứ
c Niut
ơ
n , ch
ứ
ng minh
đẳ
ng th
ứ
c (1,00
đ
i
ể
m)
Ta có :
200
100
100
199
99
100
101
1
100
100
0
100
100100
...)1( xxxxxx
C
C
C
C
++++=+ 0,25
Lấy đạo hàm 2 vế ta suy ra :
[
]
199
100
100
100
1
100
99
0
100
100
200...101100)21()1(100 xxxxxx
C
C
C
+++=++
0,50
Thay x= –
2
1ta suy ra B = 0
0,25
V.b
2,00
1
Gi
ả
i b
ất ph
ương tr
ình (1,00
đ
i
ể
m)
Đ
i
ề
u ki
ệ
n
–
1 < x < 0
0,25
B
ất ph
ương tr
ình
đ
ã
cho t
ươ
ng
đươ
ng v
ớ
i :
–2x < 024)1(
22
>++⇔+ xxx
0,25
⇔
x <–2 – 3 hoặc x > –2+ 3 . 0,25
Kết hợp với điều kiện ta được –2+
3
< x < 0
0,25
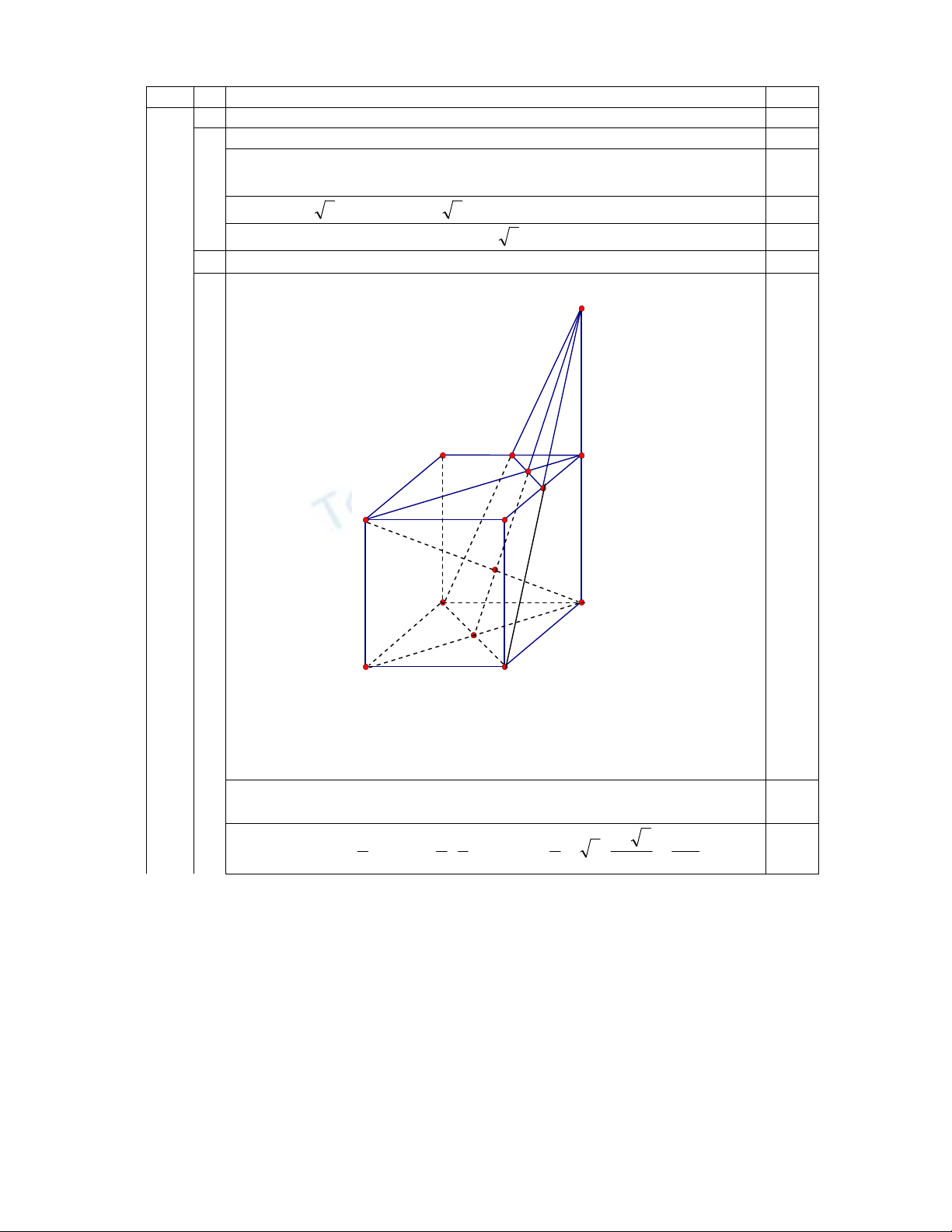
2 Chứng minh AC’
⊥
(BDMN). Tính V
A.BDMN
(1,00 điểm )
Gọi O là tâm của đáy ABCD, S là điểm đối xứng của A qua A’ . Khi đó
S,M,D thẳng hàng và M là trung điểm của SD; S,N,B thẳng hàng và N là
trung điểm của SB.
Từ hai tam giác đồng dạng SAO và ACC’ ta suy ra AC’ ⊥ SO (1)
0,25
Vì BD
⊥
AC , BD
⊥
AA’
⇒
BD
⊥
(ACC’A’)
⇒
BD
⊥
AC’ (2)
Từ (1) và (2) suy ra AC’ ⊥ (BDMN)
0,25
Ta có: V
A.BDMN
=
4
3V
S.ABD
=
4
3.
3
1SA.S
ABD
=
4
1
.
a
3
.
16
3
4
3
32
aa =
0,50
========== Hết ============
M
N
S
A'
D'
B'
C'
O
A
D
C
B