Đề số 0010
ĐỀ THI MINH HỌA KỲ THI THPT QUỐC GIA NĂM 2020
Môn: TOÁN
Thời gian làm bài: 90 phút
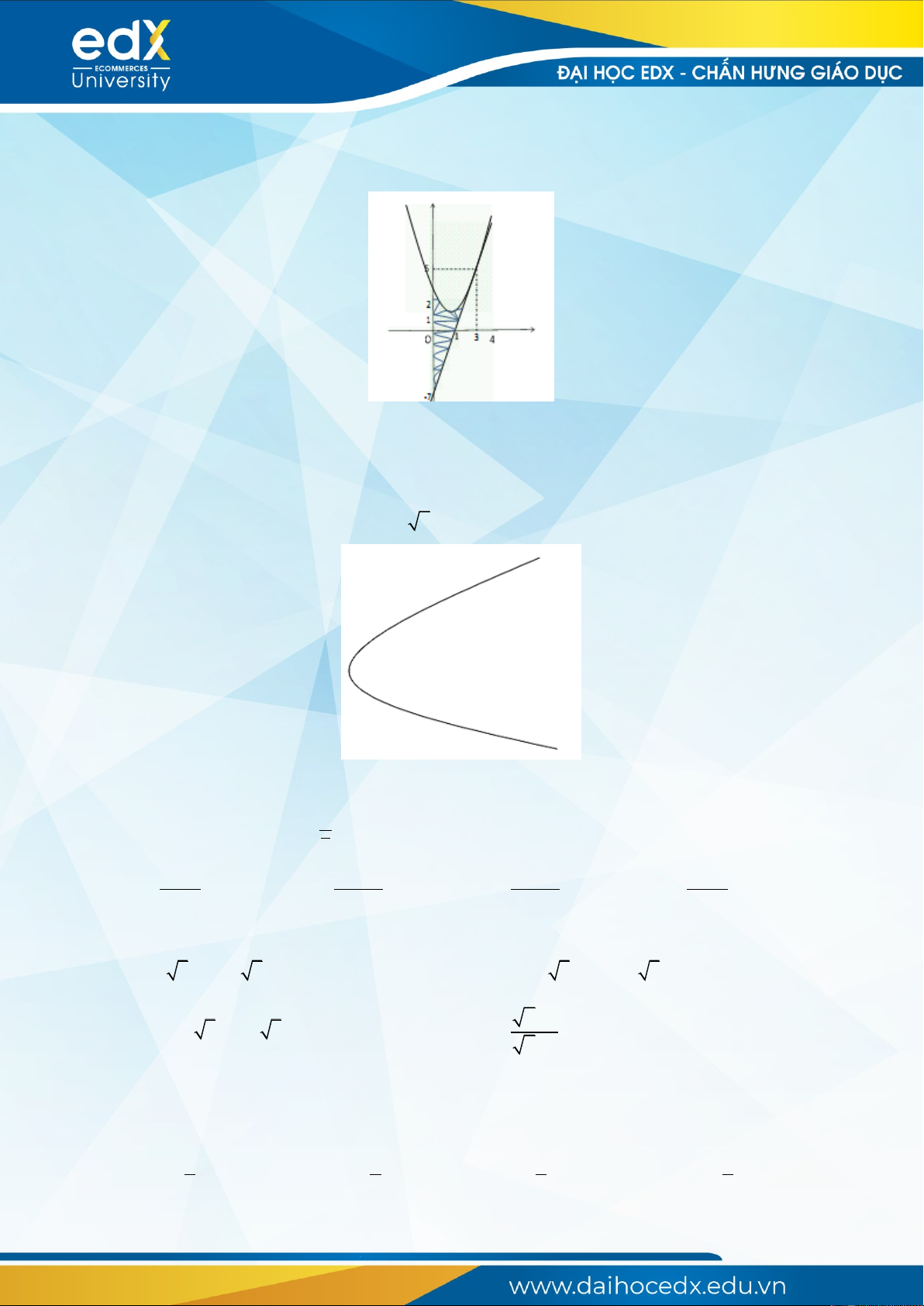
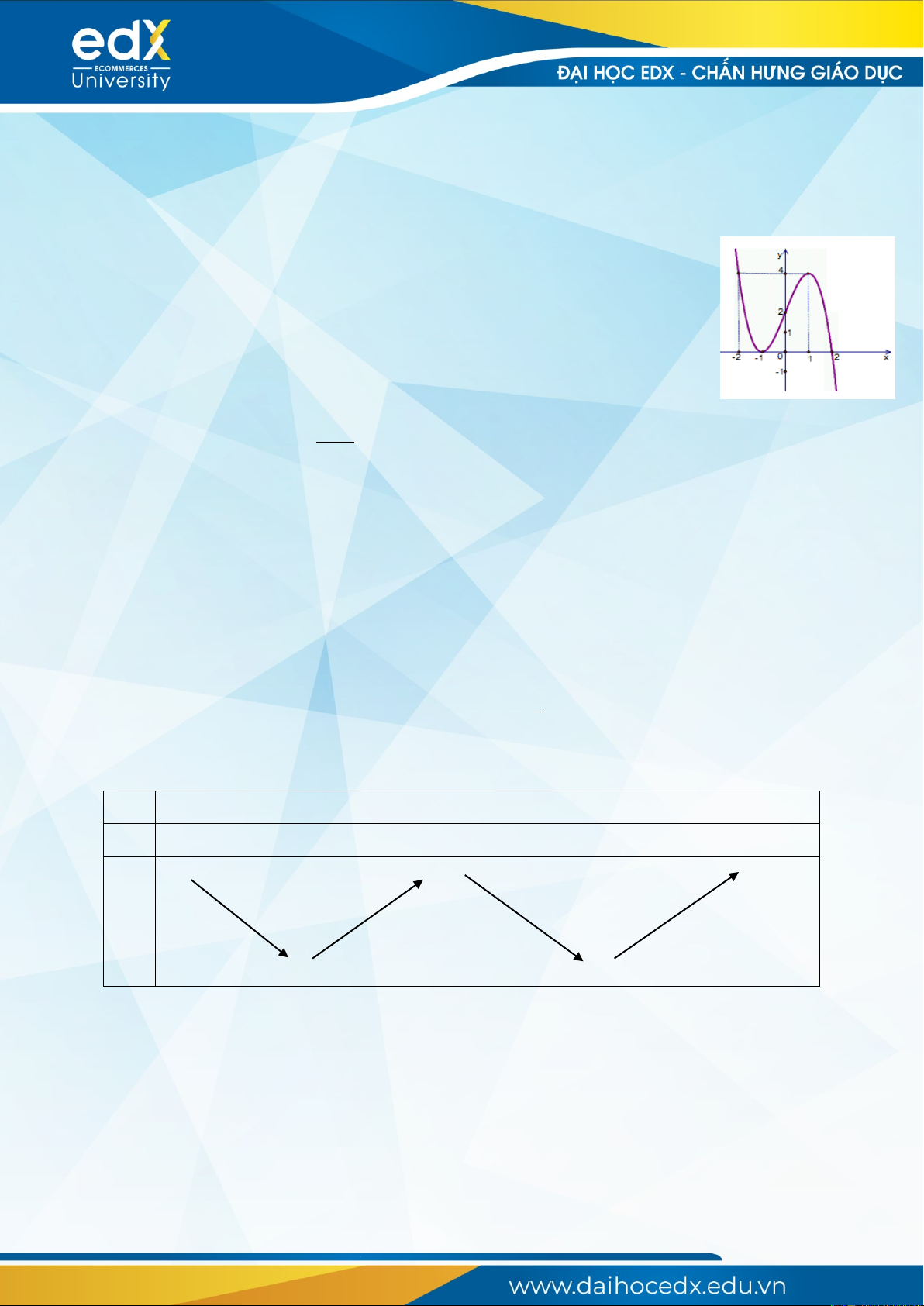
Câu 1: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số
nào?
A.
3
y x 3x 2
B.
3
y x 3x 1
C.
42
y x x 1
D.
3
y x 3x 1
Câu 2: Cho hàm số
fx
ygx
với
, có
x
lim f x 1

và
x
lim g x 1
 
.
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận ngang
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang
C. Đồ thị hàm số có thể có nhiều hơn một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
y1
và
y1
Câu 3: Hỏi hàm số
4
y 4x 1
nghịch biến trên khoảng nào?
A.
;6
B.
0; 
C.
1;
2




D.
;5
Câu 4: Cho hàm số
y f x
xác định, liên tục trên
¡
và có bảng biến thiên:
x

1
0 1

y'
0 + 0
0 +
y


3
4

Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng -3.
C. Hàm số có giá trị lớn nhất bằng

và giá trị nhỏ nhất bằng -4.
D. Hàm số đạt cực đại tại
x0
và đạt cực tiểu tại
x1
Câu 5: Tìm giá trị cực tiểu
CT
y
của hàm số
32
y x 3x 2
A.
CT
y4
B.
CT
y1
C.
CT
y0
D.
CT
y2
Câu 6: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
2
f x 2 x x
A.
min 2
max 2

B.
min 3
max 2

C.
min 2
max 3

D.
min 2
max 4

Câu 7: Cho hàm số
x1
y2x 1

có đồ thị (C) cà đường thẳng
d : y x m
. Tìm m để d luôn
cắt (C) tại 2 điểm phân biệt A, B.
A.
m5
B.
m0
C.
m1
D.
m¡
Câu 8: Cho hàm số
3 2 3
31
y x mx m
22
có đồ thị
m
C
. Tìm tất cả giá trị thực của m để
đồ thị
m
C
có hai điểm cực đại là A và B thỏa mãn AB vuông góc đường thẳng
d : y x
A.
1
m2

hoặc
m0
B.
m2
hoặc
m0
C.
1
m2

D.
m2
Câu 9: Cho hàm số
2
5x 3
yx 4x m

với m là tham số thực. Chọn khẳng định sai:
A. Nếu
m4
đồ thị hàm số có một tiệm cận ngang.
B. Nếu
m4
đồ thị hàm số có một tiệm cận ngang và một tiệm cận đứng.
C. Nếu
m4
đồ thị hàm số có ít nhất một tiệm cận đứng và một tiệm cận ngang.
D. Với mọi m hàm số luôn có hai tiệm cận đứng.
Câu 10: Người ta cần chế tạo một ly dạng hình cầu tâm O, đường kính 2R. Trong hình cầu
có một hình trụ tròn xoay nội tiếp trong hình cầu. Nước chỉ chứa được trong hình trụ. Hãy
tìm bán kính đáy r của hình trụ để ly chứa được nhiều nước nhất.
A.
R6
r3
B.
2R
r3
C.
2R
r3
D.
R
r3
Câu 11: Tìm tất cả các giá trị thực của tham số m để hàm số
cot x 2
ycotx m
đồng biến trên
khoảng
;
42




A.
m0
hoặc
1 m 2
B.
m0
C.
1 m 2
D.
m2
Câu 12: Giải phương trình
2
3
log x 1 1
A.
x2
B.
x4
C.
x2
D.
x6
Câu 13: Tính đạo hàm của hàm số
7
y log x
A.
1
y' x ln5
B.
1
y' x ln 7
C.
1
y' x
D.
x
13
y' ln13
Câu 14: Giải phương trình
2
log 3x 1 3
A.
x 14
B.
1x3
3
C.
x3
D.
10
x3
Câu 15: Tìm tập xác định D của hàm số
32
y ln x 4x
A.
D 4; 
B.
D 1;3
C.
D ; 1 3; 
D.
D 1;3
Câu 16: Đồ thị dưới đây là đồ thị của hàm số nào trong 4 đáp án sau:
A.
x
y2
B.
x
y3
C.
x
y4
D.
2
y 2x
Câu 17: Cho biểu thức
3
2log a 2
5a
B 3 log a .log 25
với a dương, khác 1. Khẳng định nào sau
đây là khẳng định đúng?
A.
2
B a 4
B.
B 2a 5
C.
2
a4
log B 1
D.
B3
Câu 18: Tính đạo hàm của hàm số
A.
x4
y' x 4 ln 2
B.
8
y' x 4 ln 2
C.
2
8
y' x 4 ln 2
D.
2
2
8
y' x 4 ln 2
Câu 19: Cho
33
log 15 a,log 10 b
. Tính
9
log 50
theo a và b.
A.
9
1
log 50 a b 1
2
B.
9
log 50 a b 1
C.
9
log 50 a b
D.
9
log 50 2a b
Câu 20: Cho bất phương trình
2
4 2 1
2
log x log 2x 1 log 4x 3 0
. Chọn khẳng định
đúng:
A. Tập nghiệm của bất phương trình là chứa trong tập
2; 
B. Nếu x là một nghiệm của bất phương trình thì
22
log x log 3
C. Tập nghiệm là
1x3
2
D. Tập nghiệm của bất phương trình là
1 x 3
Câu 21: Một người gởi 100 triệu đồng vào ngân hàng theo kì hạn một năm với lãi suất 1,75%
năm thì sau bao nhiêu năm người đó thu được một số tiền là 200 triệu. Biết rằng tiền lãi sau
mỗi năm được cộng vào tiền gốc trước đó và trở thành tiền gốc của năm tiếp theo. Đáp án
nào sau đây gần số năm thực tế nhất.
A. 41 năm B. 40 năm C. 42 năm D. 43 năm
Câu 22: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
y f x , y g x
và hai đường thẳng
x a,x b a b
là:
A.
b
a
S f x g x dx
B.
b
a
S f x g x dx
C.
b2
a
S f x g x dx
D.
b
a
S f x g x dx
Câu 23: Cho hàm số
4
2
2x 3
fx x
. Chọn phương án đúng:
A.
3
2x 3
f x dx C
3x
B.
3
2x 3
f x dx C
3x
C.
33
f x dx 2x C
x
D.
3
2x 3
f x dx C
3 2x
Câu 24: Tính
8
0
I sin x.sin 3xdx
A.
21
I4
B.
21
I4
C.
21
I8
D.
21
I8
Câu 25: Tính
5
2
0
x
J 1 2sin dx
4




là:
A.
8
J15
B.
15
J8
C.
16
J15
D.
15
J16
Câu 26: Tính
12
0
I tan 4xdx
:
A.
1
I ln 2
2
B.
1
I ln 2
3
C.
1
I ln 2
4
D.
1
I ln 2
5
Câu 27: Ở hình bên, ta có parabol
2
y x 2x 2
, tiếp tuyến với nó tại điểm
M 3;5
. Diện
tích phần gạch chéo là:
A. 9 B. 10 C. 12 D. 15
Câu 28: Một cái chuông có dạng như hình vẽ. Giả sử khi cắt chuông bởi mặt phẳng qua trục
của chuông, được thiết diện có đường viền là một phần parabol ( hình vẽ ). Biết chuông cao
4m, và bán kính của miệng chuông là
22
. Tính thể tích chuông?
A.
6
B.
12
C.
3
2
D.
16
Câu 29: Nếu
z 2i 3
thì
z
z
bằng:
A.
5 6i 2i
11
B.
5 12i
13
C.
5 12i
13
D.
3 4i
7
Câu 30: Số nào trong các số phức sau là số thực
A.
3 i 3 i
B.
2 i 5 1 2i 5
C.
1 i 3 1 i 3
D.
2i
2i
Câu 31: Trong mặt phẳng phức
A 4;1 ,B 1;3 ,C 6;0
lần lượt biểu diễn các số phức
1 2 3
z ,z ,z
. Trọng tâm G của tam giác ABC biểu diễn số phức nào sau đây?
A.
4
3i
3
B.
4
3i
3

C.
4
3i
3
D.
4
3i
3
