SỞ GIÁO DỤC VÀ ĐÀO TẠO TÂY NINH
KÌ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC 2014 – 2015
Ngày thi : 21 tháng 6 năm 2014
Môn thi : TOÁN (Không chuyên)
Thời gian : 120 phút (Không kể thời gian giao đề)
-------------------------------------------------------------------------------------
ĐỀ CHÍNH THỨC
(Đề thi có 01 trang, thí sinh không phải chép đề vào giấy thi)
Câu 1 : (1điểm Th hi n h nh
a)
A 2 5 2 5
b)
B = 2 50 3 2
Câu 2 : (1 điểm Giải hương rình:
2
2 15 0xx
.
Câu 3 : (1 điểm Giải h hương rình:
23
124
y
x
y
x


.
Câu 4 : (1 điểm Tìm a và b để đường hẳng
d : a 2 byx
h g b ng và đi
a điểm
M 1;
.
Câu 5 : (1 điểm đ h a hàm
2
2yx
.
Câu 6 : (1 điểm Lớ 9A d đ nh r ng 20 ây xanh. Đến ngày h hi n 7 bạn không
ham gia do đượ ri ậ họ b i dưỡng đội yển họ inh giỏi a nhà rường nên mỗi
bạn òn lại hải r ng hêm 3 ây mới đảm bảo kế hoạ h đặ ra. Hỏi lớ 9A bao nhiê họ
sinh.
Câu 7 : (1 điểm h ng minh r ng hương rình
luôn có hai
nghi m hân bi
1
x
,
2
x
và biể h
1 2 2 1
M 1 1x x x x
không hụ h ộ vào m.
Câu 8 : (2 điểm ho am gi AB v ông ại A đường ao AH (H h ộ B , biế
0
ACB 60
,
CH = a
. Tính AB và AC theo a.
Câu 9 : (1 điểm ho đường ròn âm O đường k nh AB đ nh, D là đường k nh hay đổi
a đường ròn (O (kh AB . Tiế yến ại B a (O ắ A và AD lần lượ ại N và M.
h ng minh gi DMN nội iế .
Câu 10 : (1 điểm ho gi AB D nội ế đường ròn âm O, b n k nh b ng a. Biế A
v ông g với BD. Tính
22
AB CD
theo a.
--- H T ---
Giám thị không giải thích gì thêm.
Họ và ên h inh : ................................................ S b o danh : .......................................
hữ k a gi m h : ........................................ hữ k a gi m h 2 : ........................
BÀI GIẢI
Câu 1 : (1điểm Th hi n h nh
a)
2
2
A 2 5 2 5 2 5 4 5 1
.
b)
B = 2 50 3 2 100 3.2 10 6 4
.
Câu 2 : (1 điểm Giải hương rình:
2
2 15 0xx
.
2
1 4.2. 15 121 0
,
11

.
1
1 11 10 5
4 4 2
x
;
2
1 11 12 3
44
x
.
ậy
5
S = ; 3
2



.
Câu 3 : (1 điểm Điề ki n
0x
.
23
124
y
x
y
x


426
124
y
x
y
x


510
23
x
y
x

5
10
23
x
y
x

1
2
43
x
y

1
2
1
x
y

(nhận .
ậy h hương rình nghi m d y nhấ
1
; ; 1
2
xy 


.
Câu 4 : (1 điểm Tìm a và b để
d : a 2 byx
h g b ng và a
M 1;
.
Đường hẳng d h g b ng
a 2 4
a6
.
Mặ kh (d đi a điểm
M 1;
nên thay
a6
,
1x
;
3y
vào
a 2 byx
.
Khi đ a :
3 6 2 .1 b
3 4 b
b7
.
ậy
a6
v à
b7
là gi r ần ìm và khi đ
d : 6 7yx
.
Câu 5 : (1 điểm đ h a hàm
2
2yx
.
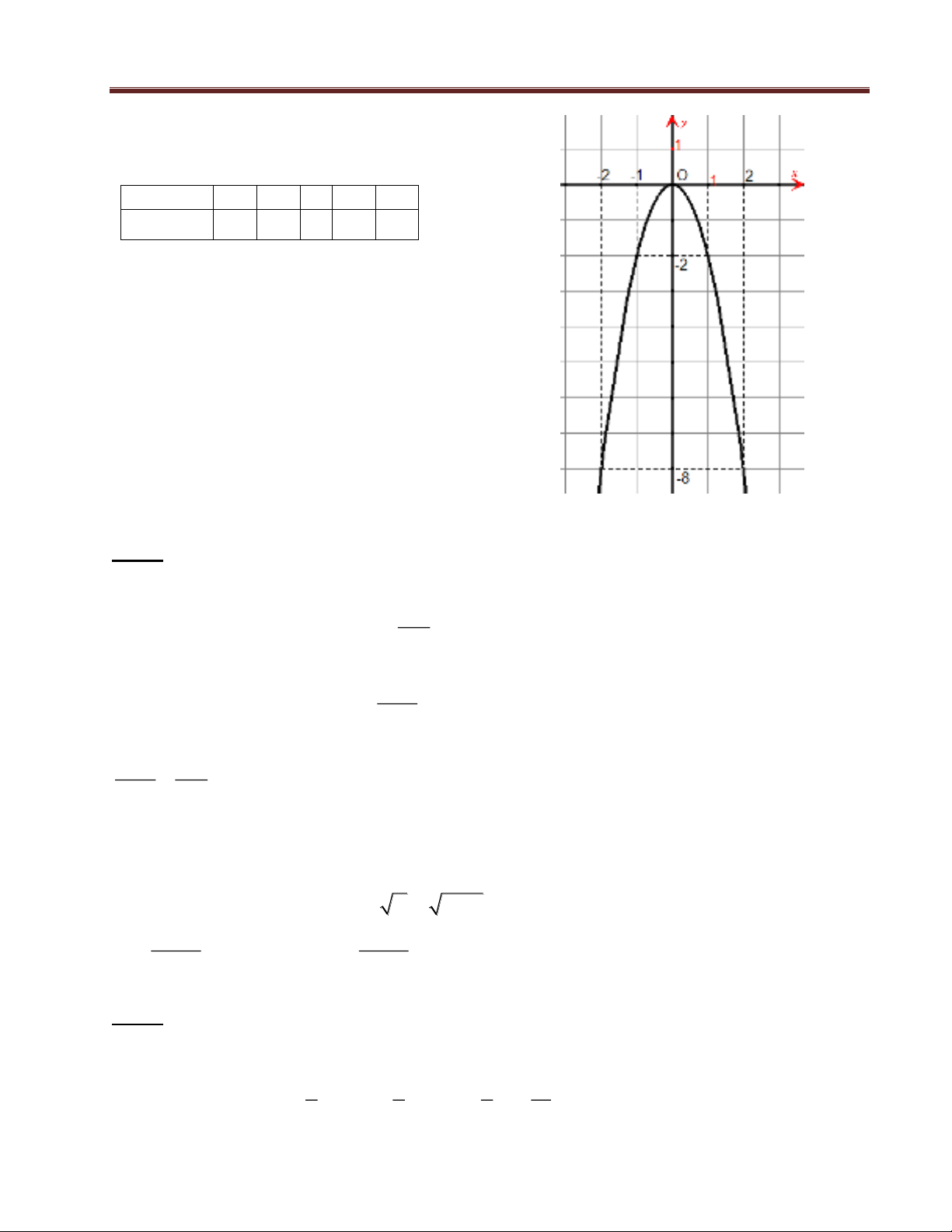
BGT
x
2
1
0
1
2
2
2yx

8
2
0
2
8
Câu 6 : (1 điểm)
Gọi họ inh lớ 9A là
x
,7xx
Z
.
Theo kế hoạ h, mỗi em hải r ng
420
x
(cây).
Trên h ế. họ inh òn lại là :
7x
.
Trên h ế, mỗi em hải r ng
420
7x
(cây).
Do lượng ây mỗi em r ng rên h ế hơn 3 ây o với kế hoạ h nên a hương rình :
420 420 37
7x
xx

420 420 7 3 7x x x x
2
3 21 2940 0xx
27 980 0xx
(chia 3)
2
7 4.1. 980 3969 0
,
3969 63
.
1
7 63 35
2
x

(nhận ;
2
7 63 28
2
x
(loại .
ậy lớ 9A 35 họ inh.
Câu 7 : (1 điểm hương rình
.
hương rình
222
' m 1 1. m 4 m 2m 1 m 4 m m 5
.
22
21 1 1 19
' m m 5 m 5 m 0, m
2 4 2 4
.
ậy hương rình l ôn hai nghi m hân bi với mọi m.
Khi đ , heo i-ét
12
2m 2xx
;
12
. m 4xx 
.
1 2 2 1 1 1 2 2 1 2 1 2 1 2
M 1 1 2x x x x x x x x x x x x x x
.
1 2 1 2
M 2 2m 2 2 m 4 2m 2 2m 8 10x x x x
(không hụ h ộ vào m .
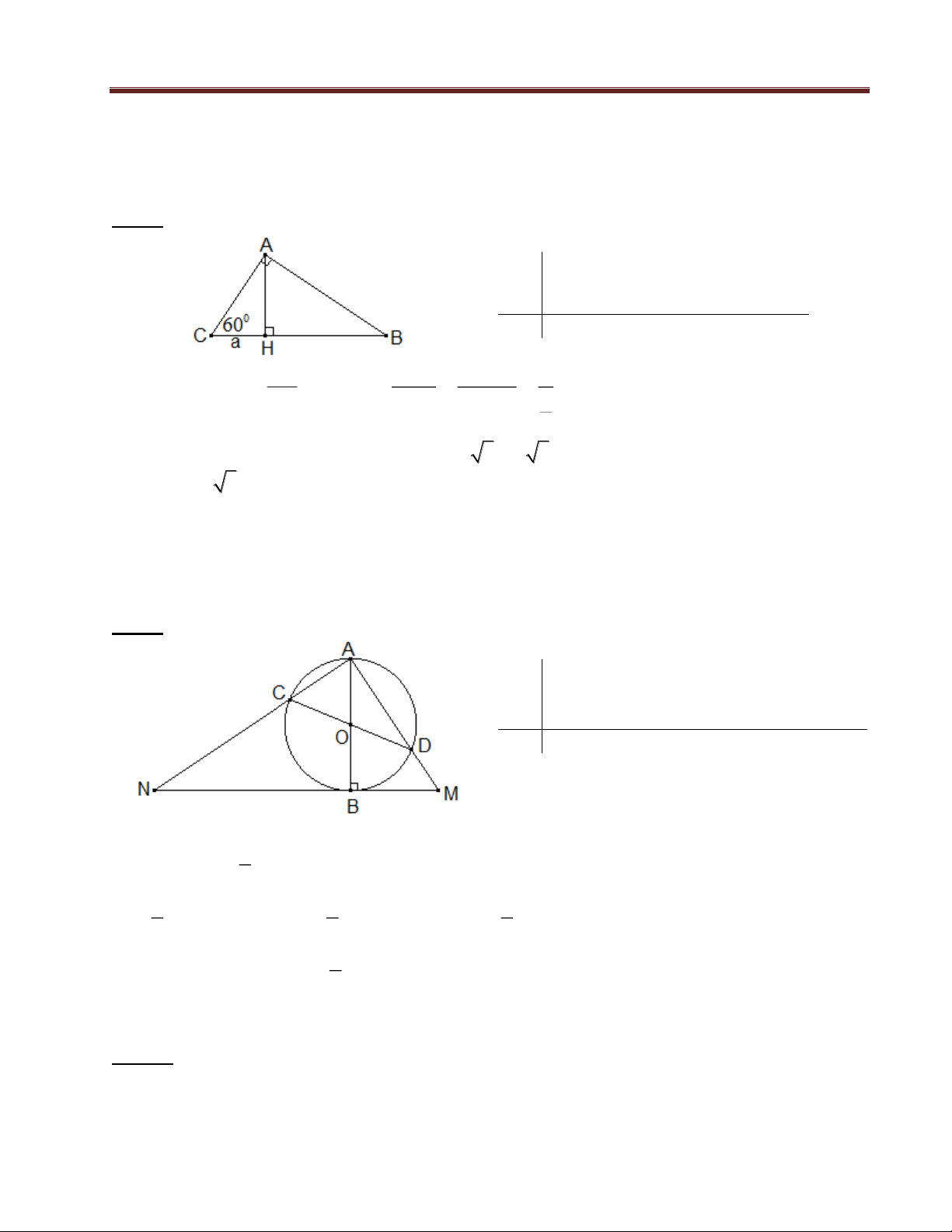
Câu 8 :
GT
ABC
,
0
A 90
,
AH BC
,
0
ACB 60
,
CH = a
KL
Tính AB và AC theo a?
ACH
có
CH
cosC AC
nên
0
CH a a
AC 2a
1
cosC cos60
2
.
ABC
có
0
AB = AC.tanC = 2a.tan60 2a. 3 2 3a
.
ậy
AB = 2 3a
,
AC 2a
.
Câu 9 : (1 điểm)
GT
(O đường k nh AB đ nh, đường
k nh D hay đổi, MN là iế yến
ại B a (O .
KL
T gi DMN nội iế
h ng minh gi DMN nội iế
Ta có :
1
ADC AC
2
sñ
.
1 1 1
N ADB BC ACB BC AC
2 2 2
sñ sñ sñ sñ sñ
.
ADC N
( ùng b ng
1AC
2
sñ
).
T gi DMN nội iế đượ (g ngoài b ng g đ i rong .
Câu 10 : (1 điểm)
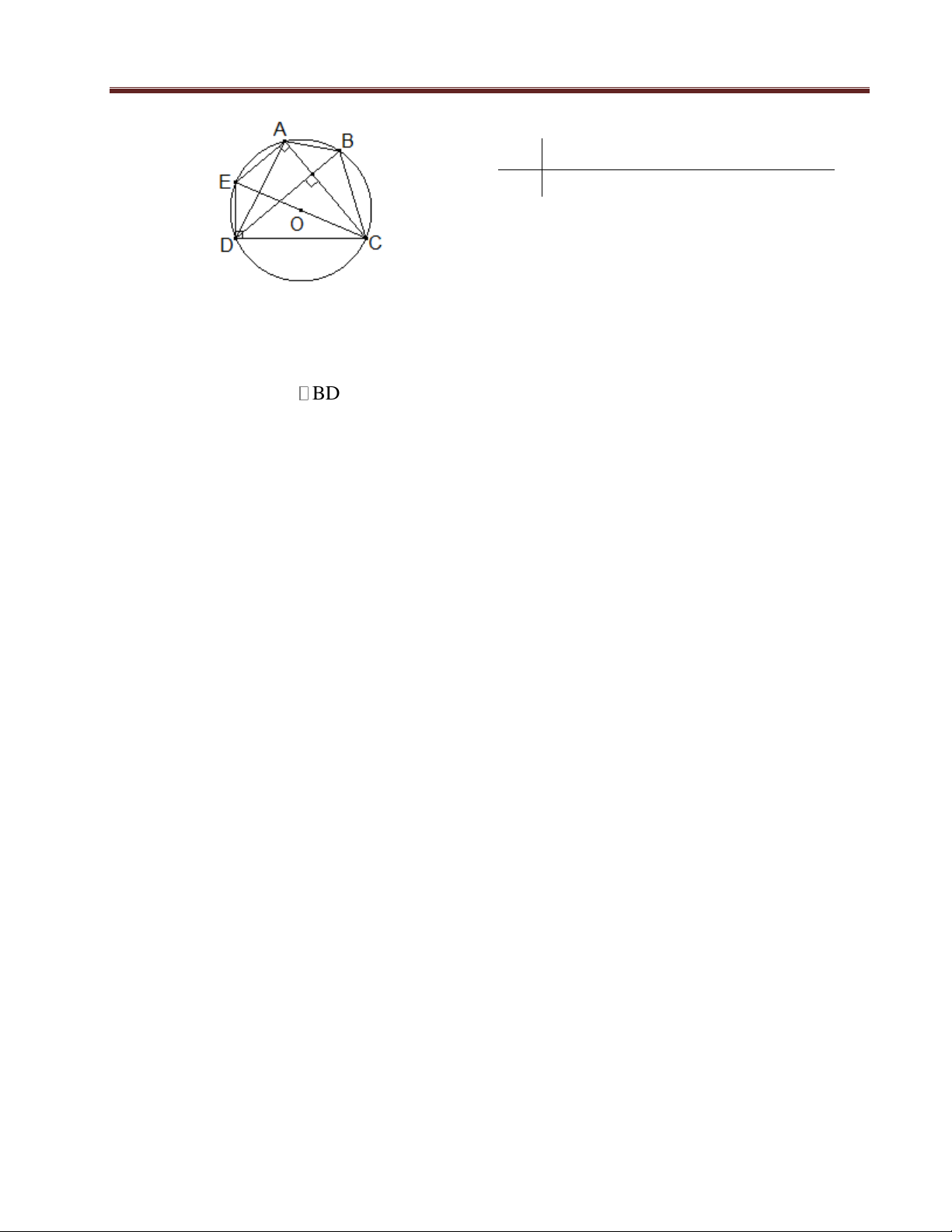
GT
AB D nội iế
O; a
,
AC BD
KL
Tính
22
AB CD
theo a.
Tính
22
AB CD
theo a.
đường k nh E a đường ròn (O .
Ta có :
0
EAC 90
,
0
EDC 90
(g nội iế hắn đường k nh E .
AC AE AE BD
AC BD ( )gt


ABDE là hình hang ân (hình hang nội iế (O
AB = DE
( ạnh bên hình hang ân .
2
2 2 2 2 2 2
AB + CD = DE + DC = EC 2a 4a
(do
EDC
v ông ại D .
ậy
2 2 2
AB CD 4a

.
--- H T ---