DFS-Apriori: Khai Thác Nhanh Tập Phổ Biến
Áp Dụng Chiến Lƣợc Tìm Kiếm Theo Chiều Sâu
Phan Thành Huấn1,2,4, Đặng Thanh Minh1,4, Nguyễn Nhƣ Đồng3
1Khoa Toán – Tin học, Trƣờng Đại học Khoa học Tự nhiên, ĐHQG.HCM-VN
2Bộ môn Tin học, Trƣờng Đại học Khoa học Xã hội và Nhân văn, ĐHQG.HCM-VN
3Trung tâm Giáo dục Nghề nghiệp – Giáo dục Thƣờng xuyên, Tp. Thủ Đức
4Đại học Quốc gia Tp. Hồ Chí Minh
Email: huanphan@hcmussh.edu.vn; minhthanhdang1982@gmail.com; dongnhunguyen74@gmail.com
Tóm tắt - Khai thác tập phổ biến là giai đoạn cốt lõi trong khai
thác luật kết hợp từ dữ liệu giao dịch nhị phân. Agrawal cùng
đồng sự đề xuất thuật toán Apriori . Đây là thuật toán cơ sở cho
nhiều cải tiến, cũng như được sử dụng khai thác trên nhiều loại
dữ liệu khác nhau. Ngoài ra, những năm gần đây thuật toán
Apriori là thuật toán được nhiều nhà nghiên cứu lựa chọn để mở
rộng cho khai thác tập phổ biến từ dữ liệu lớn trên môi trường
phân tán. Thuật toán Apriori dựa theo chiến lược tìm kiếm theo
chiều rộng (Breadth First Search – BFS) – điều này làm hạn chế
trong thực hiện tính toán phân tán. Trong bài viết này, nhóm tác
giả khảo sát một số thuật toán Apriori cải tiến và trình bày cách
tiếp cận mới cải tiến hiệu quả thuật toán Apriori dựa theo chiến
lược tìm kiếm theo chiều sâu (Depth First Search – DFS) – dễ
dàng mở rộng trên môi trường tính toán phân tán. Đồng thời,
thuật toán đề xuất kỹ thuật rút gọn các ứng viên, tính nhanh độ
phổ biến của ứng viên và biểu diễn dữ liệu dạng bit - giúp đẩy
nhanh tốc độ tính toán và giảm thiểu truy xuất dữ liệu. Thuật
toán cải tiến được gọi là DFS-Apriori. Nhóm tác giả tiến hành
thực nghiệm thuật toán trên bộ dữ liệu thực của UCI và dữ liệu
giả lập của trung tâm nghiên cứu IBM Almaden, cho thấy thuật
toán cải tiến hiệu quả.
Từ khóa – luật kết hợp, tập phổ biến, thuật toán DFS-Apriori.
I. GIỚI THIỆU
Năm 1993, Agrawal cùng đồng sự đề xuất mô hình đầu tiên
của bài toán khai thác luật kết hợp – khai thác luật kết hợp trên
dữ liệu giao dịch (DLGD) nhị phân [1]. Khai thác luật kết hợp
là khai phá các luật kết hợp có độ phổ biến (support) cũng nhƣ
độ tin cậy (confidence) lớn hơn hoặc bằng một ngƣỡng phổ
biến tối thiểu (minsup) và ngƣỡng tin cậy tối thiểu (minconf).
Bài toán đƣợc chia thành hai pha:
Pha 1: Tìm tất cả các kết hợp thỏa ngƣỡng phổ biến tối
thiểu minsup (sinh tập phổ biến FI - Frequent Itemset);
Pha 2: Sinh luật kết hợp lần lƣợt từ các kết hợp thỏa
minsup ở pha 1 và các luật kết hợp này phải thỏa ngƣỡng tin
cậy tối thiểu minconf.
Sau đó, Agrawal cùng đồng sự tập trung hƣớng giải quyết
cho pha 1 và nhóm đã đề xuất thuật toán Apriori [2] cho khai
thác tập phổ biến. Đây là thuật toán then chốt, quan trọng trong
khai thác luật kết hợp. Thuật toán tiếp cận sinh các kết hợp phổ
biến với chiến lƣợc tìm kiếm theo chiều rộng (Breadth First
Search – BFS) dễ dàng cài đặt và song song hóa nhằm nâng
cao hiệu năng; thuật toán tốn nhiều lần quét dữ liệu và có độ
phức tạp dạng hàm mũ. Chính vì vậy, Apriori là thuật toán
đƣợc nhiều nhà nghiên cứu cải tiến và áp dụng khai phá trên
nhiều loại dữ liệu khác nhau: chuỗi [3], định lượng [4], đồ thị
[5], thuộc tính có trọng số [6],…
Qua khảo sát các nghiên cứu liên quan đến cải tiến thuật
toán Apriori khai thác tập phổ biến trên DLGD nhị phân, gồm
hai hướng tiếp cận chính:
Định dạng dữ liệu theo chiều ngang: Đây là định dạng
theo thuật toán Apriori gốc. Các thuật toán cải tiến Apriori
thƣờng sử dụng chiến lƣợc rút gọn giao dịch và rút gọn
không gian sinh các ứng viên tiềm năng k-itemset. Tuy
nhiên, vấn đề tính độ phổ biến của k-itemset vẫn chƣa thật
sự hiệu quả.
Định dạng dữ liệu theo chiều dọc: Năm 1995, Savasere
[7] cùng đồng sự đề xuất thuật toán Parition sử dụng định
dạng dữ liệu theo chiều dọc. Định dạng này, giúp tính độ
phổ biến dễ dàng và hạn chế đối với DLGD có mật độ cao.
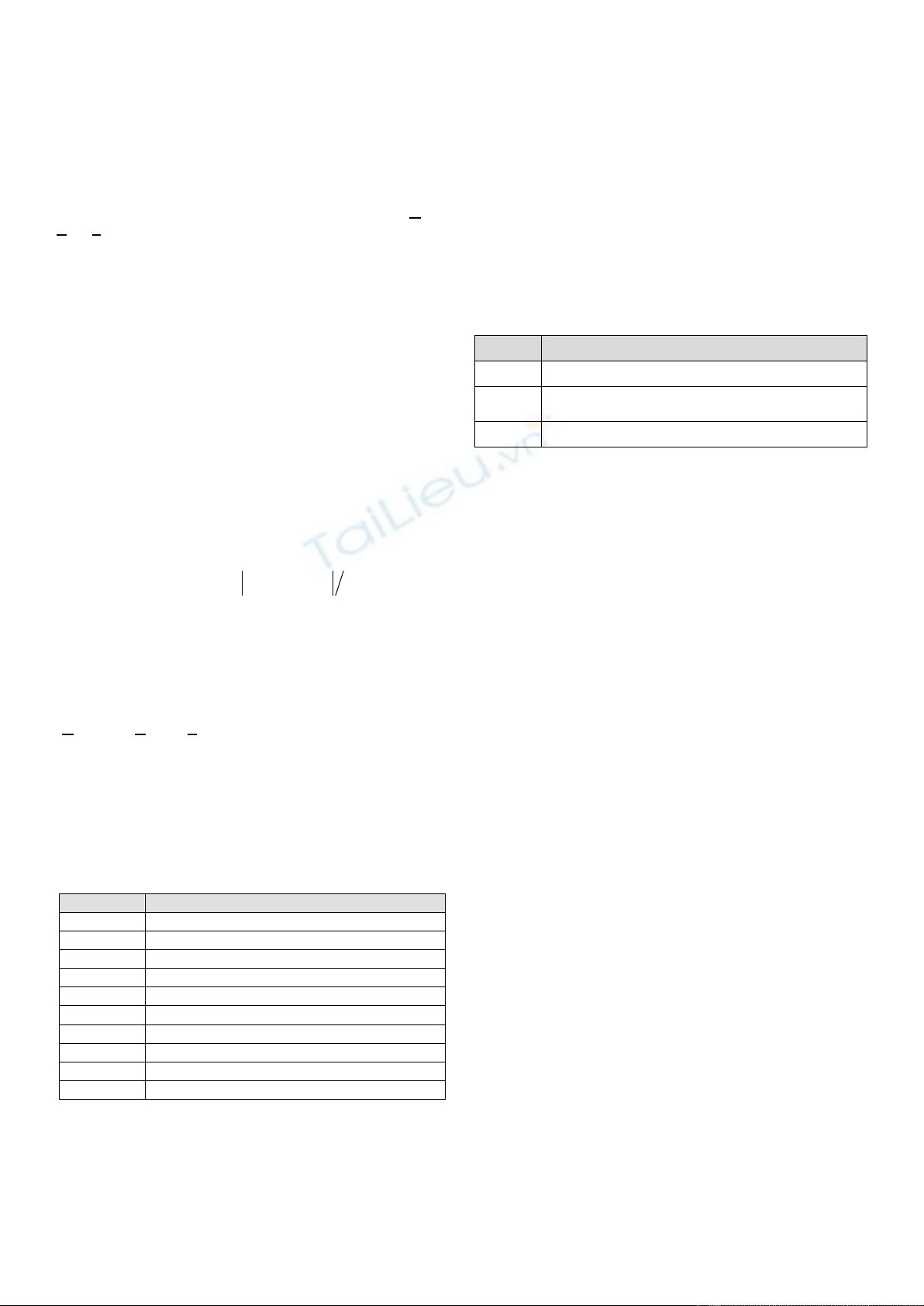
Bảng 1. Một số công trình cải tiến thuật toán Apriori [7-16]
Tác giả
đứng đầu
Thuật toán
Định dạng
dữ liệu
Năm
A. Savasere
Partition
dọc
1995
J. Lei
HDO-Apriori
ngang
2006
W.Yu
RATT
ngang
2008
Y. Guo
IApriori
dọc
2010
J. Singh
SOT-Apriori
ngang
2013
H. Singh
MBAT
ngang
2013
M. A. Maolegi
M-Apriori
dọc
2014
V.Vijayalakshmi
CBTRA
ngang
2015
S. Aditya
LOT-Apriori
ngang
2017
L. Xu
MD-Apriori
dọc
2019
Bảng 1, liệt kê một số thuật toán cải tiến Apriori. Các đặc
trƣng của thuật toán cải tiến: i) rút gọn giao dịch dựa vào số
lƣợng items trên mỗi giao dịch – SOT-Aprioir [11], CBTRA
[14], LOT-Apriori [15] ; ii) rút gọn tập ứng viên tiềm năng –
Partition [7], HDO-Apriori [8], Iapriori [11], M-Apriori [13],
MD-Apriori [16]; iii) giảm bƣớc tính độ phổ biến – RAAT [9],
MBAT [12]; iv) phân chia dữ liệu thành nhiều phần – Parition
[7], MD-Apriori [16].
Ngoài ra, thuật toán tựa Apriori cũng đƣợc nhiều nhà
nghiên cứu quan tâm mở rộng thực hiện khai thác dữ liệu lớn
trên môi trƣờng phân tán. Gần đây, Shashi cùng đồng sự đề
xuất thuật toán EAFIM [19] khai thác trên môi trƣờng phân
tán Spark và dựa trên thuật toán Apriori gốc, thuật toán
EAFIM cũng cho thấy hiệu quả hơn thuật toán R-Apriori [18],
YAFIM [17].
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
135
Nhóm tác giả thấy rằng, các thuật toán cải tiến trên chƣa
quan tâm đến thứ tự độ phổ biến của các items, rút gọn bƣớc
phát sinh ứng viên k-itemset từ tập phổ biến (k-1)-itemset.
Ngoài ra, chiến lƣợc tìm kiếm theo chiều rộng rất khó phân rã
khi mở rộng khai thác dữ liệu lớn trên các hệ thống tính toán
phân tán. Vì vậy, nhóm tác giả đề xuất tiếp cận mới trong cải
tiến hiệu quả thuật toán Apriori cho khai thác tập phổ biến trên
DLGD áp dụng chiến lƣợc tìm kiếm theo chiều sâu (Depth
First Search – DFS) – thuật toán dễ dàng mở rộng trên môi
trƣờng tính toán phân tán.
Phần 2, bài báo trình bày các khái niệm cơ bản về khai thác
tập phổ biến, thuật toán AprioriTID và phân tích ƣu, nhƣợc
điểm. Phần 3, đề xuất thuật toán khai thác nhanh tập phổ biến
theo hƣớng tiếp cận theo chiều sâu DFS-Apriori; kết quả thực
nghiệm đƣợc trình bày trong phần 4; kết luận và hƣớng phát
triển đƣợc trình bày trong phần 5.
II. CÁC KHÁI NIỆM CƠ BẢN
A. Khai thác tập phổ biến
Cho I = {i1, i2,..., im} là tập gồm m thuộc tính, mỗi thuộc
tính gọi là item. Tập các item X ={i1, i2,..., ik}, ij I (1
j
k)
gọi là itemset, itemset có k item gọi là k-itemset. Dữ liệu giao
dịch T = {t1, t2,..., tn} gồm n giao dịch, mỗi giao dịch tk ={ik1,
ik2,..., ikm}, ikj
I (1
kj
m).
Định nghĩa 1: Độ phổ biến (support) của itemset X I, ký
hiệu sup(X) - tỷ lệ giữa số giao dịch trong T có chứa X và n
giao dịch.
Định nghĩa 2: Cho X I, X gọi là itemset phổ biến –
nếu sup(X) ≥ minsup, trong đó minsup là ngƣỡng phổ biến tối
thiểu (do người dùng chỉ định). Ký hiệu FI là tập hợp chứa các
itemset phổ biến.
Một số tính chất của itemset phổ biến: đây là các tính
chất nền tảng sử dụng cho việc rút gọn không gian tìm kiếm –
các tính chất này đƣợc gọi là tính chất Apriori/ bao đóng giảm
(Downward Closure Property - DCP).
Tính chất 1: (độ phổ biến của tập con) Cho X, Y I, nếu X
Y thì sup(X) sup(Y);
Tính chất 2: Một itemset con khác rỗng của một itemset
phổ biến cũng là itemset phổ biến - XY, sup(Y) ≥ minsup:
sup(X) ≥ minsup;
Tính chất 3: Một itemset chứa một itemset không phổ biến
cũng là itemset không phổ biến - X Y, sup(X) < minsup:
sup(Y) < minsup.
Bảng 2. Dữ liệu giao dịch T dùng cho Ví dụ
TID
Items
t1
A
C
E
F
t2
A
C
G
t3
E
H
t4
A
C
D
F
G
t5
A
C
E
G
t6
E
t7
A
B
C
E
t8
A
C
D
t9
A
B
C
E
G
t10
A
C
E
F
G
Ví dụ 1: Dữ liệu giao dịch trong Bảng 1, có 8 item riêng
biệt I = {A, B, C, D, E, F, G, H} và tập giao dịch Ƭ = {t1, t2,
t3, t4, t5, t6, t7, t8, t9, t10} với giá trị ngƣỡng phổ biến tối
thiểu minsup = 0,50, ta có:
Theo tính chất 1: X ={G, A, C}, sup(GAC) = 0,50 – độ
phổ biến lần lƣợt các tập con của X: sup(A) = sup(C) sup(AC)
= 0,80; sup(G) = sup(GA) = sup(GC) = 0,50.
Theo tính chất 2: các tập con của X ={G, A, C} cũng phổ
biến; ta thấy độ phổ biến của các tập con của X đều lớn hơn
hoặc bằng ngƣỡng minsup.
Theo tính chất 3: Y = {F} thì sup(F) = 0,20 < minsup - ”Y
= {F} itemset không phổ biến ngƣỡng minsup”. Khi đó, các
tập cha của Y cũng không phổ biến, nghĩa là Z = {F, E} cũng
không phổ biến, sup(FE) = 0,20 < minsup.
Bảng 3. FIs trên dữ liệu giao dịch T, minsup = 0,50
k-itemset
Tập phổ biến FIs (#FIs = 11)
1
(G; 0,50), (E; 0,70), (A; 0,80), (C; 0,80)
2
(GA; 0,50), (GC; 0,50), (EA; 0,50), (EC; 0,50),
(AC; 0,80)
3
(GAC; 0,50), (EAC; 0,50)
Ở Bảng 3, trình bày k-itemset phổ biến trên DLGD với
ngƣỡng minsup = 0,50; các k-itemset phổ biến đƣợc sắp xêp
tăng dần theo độ phổ biến của các items
(H
B
D
F
G
E
A
C) và có 11 itemset phổ biến.
B. Thuật toán Apriori và AprioriTID
Thuật toán Apriori do Agrawal cùng đồng sự đề xuất năm
1994 [2], đƣợc đánh giá mang tính chất lịch sử trong khai thác
luật kết hợp. Apriori là thuật toán nền tảng để tìm các tập phổ
biến sử dụng phƣơng pháp sinh ứng viên. Thuật toán có đặc
điểm là tìm kiếm theo chiều rộng sử dụng tính chất Apriori:
bất kỳ (k-1)-itemset không phổ biến thì nó không thể là tập
con của k-itemset phổ biến.
Một số ký hiệu trong thuật toán Apriori:
Lk: tập chứa k-itemset phổ biến;
Ck: tâp ứng viên tiềm năng k-itemset;
Mã giả thuật toán Apriori
Đầu vào: Tập giao dịch Ƭ, ngƣỡng minsup
Đầu ra: Tập kết hợp nối liền phổ biến FI
1:
L1 = {1-itemset}
2:
For (k = 2; Lk-1 ; k++) do
3:
Ck = AprioriGen(Lk-1)
4:
For each t Ƭ do
5:
Ct = subset(Ck, t)
6:
For each c Ct do
7:
c.count ++
8:
Lk = {c Ck| c.count minsup}
9:
FI = k Lk
10:
Trả về FI
Dòng 1, tập L1 chứa các item thỏa minsup; dòng 2 đến 8,
phát sinh k-itemset phổ biến; dòng 3 sinh tập Ck ứng viên chứa
k-itemset từ tập Lk-1 chứa các (k-1)-itemset phổ biến; dòng 4
đến 7, với mỗi giao dịch t, xác định các ứng viên tiềm năng từ
Ck đƣợc chứa trên giao dịch này và lƣu vào Ct. Độ phổ biến
của từng ứng viên tiềm năng Ck đƣợc tính toán theo Ct; dòng
8, lọc ứng viên k-itemset thỏa ngƣỡng minsup đƣa vào Lk.
Thủ tục AprioriGen - sinh các ứng viên k-itemset tiềm
năng Ck từ tập (k-1)-itemset Lk-1.
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
136
Mã giả thủ tục AprioriGen
Đầu vào: Tập chứa các (k-1)-itemset phổ biến Lk-1
Đầu ra: Tập ứng viên k-itemset Ck
1:
Ck = {X X’| X, X’ Lk-1, |XX’| = k - 2}
2:
For each itemset c Ck do
3:
For each (k-1)-subset s of c do
4:
If (s Lk-1) then
5:
Ck = Ck - c
6:
Trả về Ck
Ưu điểm: Thuật toán dựa trên tính chất Apriori là bất kỳ
itemset con nào của itemset phổ biến cũng là itemset phổ biến.
Vì vậy, trong quá trình đi tìm tập ứng viên, thuật toán chỉ cần
dùng đến tập ứng viên vừa xuất hiện ở bƣớc ngay trƣớc đó,
không cần dùng đến tất cả tập ứng viên (cho đến thời điểm
đó). Nhờ vậy, bộ nhớ đƣợc giải phóng đáng kể.
Nhược điểm: Thuật toán phải quét dữ liệu (maxlen+1) lần,
với maxlen là chiều dài của itemset phổ biến dài nhất. Thuật
toán Apriori giảm không gian dựa vào tính chất Apriori. Tuy
nhiên, khi số itemset phổ biến đƣợc sinh ra lớn, maxlen lớn
hay ngƣỡng phổ biến tối thiểu minsup nhỏ sẽ dẫn đến việc
phát sinh ra rất nhiều ứng viên và phải duyệt dữ liệu rất nhiều
lần, thuật toán có chi phí cao.
Trong công trình [2], Agrawal cùng đồng sự đề xuất thêm
thuật toán cải tiến AprioriTID – độ phổ biến của ứng viên tiềm
năng đƣợc tính dựa trên tập
k
C
(lƣu trữ từng dòng giao dịch
có chứa các ứng viên k-itemset theo cấu trúc <t.TID, Ct>).
Một số ký hiệu trong thuật toán AprioriTID:
Lk: tập chứa k-itemset phổ biến;
Ck: tâp ứng viên tiềm năng k-itemset;
k
C
: tập các ứng viên k-itemset đƣợc chứa trong từng giao
dịch t của DLGD;
Mã giả thuật toán AprioriTID
Đầu vào: Tập giao dịch Ƭ, ngƣỡng minsup
Đầu ra: Tập kết hợp nối liền phổ biến FI
1:
L1 = {1-itemset}
2:
1
C
= tập giao dịch Ƭ// chứa các item trong L1
3:
For (k = 2; Lk-1 ; k++) do
4:
Ck = AprioriGen(Lk-1)
5:
k
C
=
6:
For each t
1k
C
do
7:
Ct = {c Ck| (c – c[k]) t.set-of-itemset
(c – c[k-1]) t.set-of-itemset}
8:
For each c Ct do
9:
c.count ++
10:
If (Ct ) then
11:
k
C
+= <t.TID, Ct>
12:
Lk = {c Ck| c.count minsup}
13:
Trả về FI= k Lk
Để thuận tiên cho việc minh họa thuật toán AprioriTID,
nhóm tác giả hiệu chỉnh ở dòng 2 so với phiên bản gốc
(
1
C
chứa các item có trong L1 thỏa ngƣỡng minsup).
C. Minh họa thuật toán AprioriTID
Trong phần này, nhóm tác giả minh họa thuật toán
AprioriTID khai thác các itemset phổ biến:
Ví dụ 2: Cho dữ liệu giao dịch T trong Bảng 1 và giá trị
ngƣỡng minsup = 0,30.
Dữ liệu giao dịch T, có 5 item thỏa minsup: L1 = {(F; 0,30),
(G; 0,50), (E; 0,70), (A; 0,80), (C; 0,80)};
1
C
=
{<t1,{{F},{E},{A},{C}}>, <t2,{{G}, {A}, {C}}>, <t4,{{F},
{G}, {A}, {C}}>, <t5,{{G}, {E}, {A}, {C}}>, <t7,{{E}, {A},
{C}}>, <t8,{{A}, {C}}>, <t9,{{G}, {E}, {A}, {C}}>,
<t10,{{G}, {E}, {A}, {C}}>};
Bước lặp k = 2: sinh tập ứng viên 2-itemset C2 = {FG, FE,
FA, FC, GE, GA, GC, EA, EC, AC};
2
C
={<t1, {{FA}, {FC},
{EA}, {EC}, {AC}}>, <t2, {{GA}, {GC}}>, <t4,{{FA},
{FC}, {GA}, {GC}, {AC}}>, <t5, {GE}, {GA}, {GC}, {EA},
{EC}, {AC}}>, <t7, {{EA}, {EC}, {AC}}>, <t8, {{AC}}>,
<t9, {{GE}, {GA}, {GC}, {EA}, {EC}, {AC}}>, <t10,
{{GE}, {GA}, {GC}, {EA}, {EC}, {AC}}>; tập phổ biến L2 =
{(FA; 0,30), (FC; 0,30), (GE; 0,30), (GA; 0,50), (GC; 0,50),
(EA; 0,50), (EC; 0,50), (AC; 0,80)};
Bước lặp k = 3: sinh ứng viên 3-itemset C3 = {FAC, GEA,
GEC, GAC, EAC};
3
C
={<t1, {{FAC}, {GAC}}>, <t2,
{{GAC}}>, <t4, {{FAC}, {GAC}}>, <t5, {{GEA}, {GEC},
{GAC}, {EAC}}>, <t7, {{EAC}}>, <t9, {{GEA}, {GEC},
{GAC}, {EAC}}>, <t10, {{GEA}, {GEC}, {GAC},
{EAC}}>}; tập phổ biến L3 = {(FAC; 0,30), (GEA; 0,30),
(GEC; 0,30), (GAC; 0,50), (EAC; 0,50)};
Bước lặp k = 4: sinh ứng viên 4-itemset C4 = {GEAC};
4
C
={<t5, {{GEAC}}>, <t9,{{GEAC}}>, <t10, {GEAC}}>};
tập phổ biến L4 = {(GEAC; 0,30)};
Kết quả khai thác tập phổ biến trên dữ liệu giao dịch T, với
ngƣỡng minsup = 0,30 đƣợc trình bày ở Bảng 4.
Bảng 4. FIs trên dữ liệu giao dịch T, minsup = 0,30
Items
Tập phổ biến FIs (#FIs = 19)
F
(F; 0,30), (FA; 0,30), (FC; 0,30), (FAC; 0,30)
G
(G; 0,50), (GE; 0,30), (GA; 0,50), (GC; 0,50),
(GEA; 0,30),(GEC; 0,30), (GAC; 0,50), (GEAC; 0,30)
E
(E; 0,70), (EA; 0,50), (EC; 0,50), (EAC; 0,50)
A
(A; 0,80), (AC; 0,80)
C
(C; 0,80)
III. THUẬT TOÁN DFS-APRIORI
A. Thuật toán DFS-Apriori
Phần này, nhóm tác giả trình bày thuật toán DFS-Apriori
hiệu quả khai thác tập phổ biến, cải tiến từ thuật toán Apriori
và dễ dàng mở rộng trên các hệ thống tính toán phân tán:
Thứ nhất, sắp xếp các item theo thứ tự tăng dần của độ phổ
biến – sử dụng tính chất 3 cho việc rút gọn các kết hợp ở bƣớc
tiếp theo (item đầu tiên trong các kết hợp là item có độ phổ
biến nhỏ nhất).
Thứ hai, cải tiến thủ tục AprioriGen sinh các ứng viên
bằng cách sắp xếp các (k-1)-itemset phổ biến theo thứ tự và
sinh các kết hợp mới giúp giảm dƣ thừa và trùng lặp.
Thứ ba, thực hiện tính độ phổ biến cho các ứng viên tiềm
năng C theo nhóm item đầu dựa trên ma trận bit Ƭ tƣơng ứng
đƣợc rút gọn theo cột occ (vector giao dịch chứa item thứ i).
Một số ký hiệu trong thuật toán DFS-Apriori:
- L: tập thành viên chứa k-itemset thỏa minsup, mỗi thành
viên có 4 trƣờng thông tin là itemset và độ phổ biến sup,
bổ sung thêm thứ tự nhỏ nhất (min) và lớn nhất (max) của
item trong mỗi itemset thuộc Lk;
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
137
- C: tập ứng viên chứa k-itemset tiềm năng, mỗi ứng viên
có 4 trƣờng thông tin là itemset biểu diễn dạng bit, độ phổ
biến sup, thứ tự nhỏ nhất (min) và lớn nhất (max) của item
trong mỗi itemset thuộc C;
- Ƭ: tập giao dịch đƣợc biểu diễn dạng bit, mỗi giao dịch
dạng bit có thêm 3 trƣờng thông tin là |t| số lƣợng items
trong giao dịch, thứ tự nhỏ nhất (min) và lớn nhất (max) là
thứ tự item đầu, cuối trong giao dịch.
Mã giả thuật toán DFS-Apriori
Đầu vào: Tập giao dịch Ƭ, ngƣỡng minsup
Đầu ra: Tập phổ biến FI
1:
L1 = {1-itemset}; // các item thỏa minsup
2:
Ƭ = tập Ƭ chỉ chứa các item có trong L1 và có |t| > 1
//Ƭ biểu diễn dạng bit và có thứ tự theo |t|, min, max
3:
L2 = {L1L1}//2-itemset thỏa minsup
4:
FI = L1 L2
5:
For (i = 1; i < |L1|; i++) //xét item thỏa minsup
6:
L = { L2| .min == i} //nhóm item thứ i
7:
Cập nhật vector occ tƣơng ứng với item thứ i
8:
k = 3// sinh 3-itemset
9:
While (|L| > 1) do //sinh itemset phổ biến
10:
C = AprioriGenStar(L)
11:
For each c C do //tính sup theo nhóm giao dịch
12:
j = 1
13:
While (k t[j].|t| t[j].min c.min)//t Ƭ
14:
If (occ[j]==1 c.max t[j].max) then
15:
If (c.itemset==c.itemset AND t[j].itemset) then
16:
c.sup += 1/n
17:
j++
18:
Lnext = {c C| c.sup minsup}//lọc ứng viên thỏa
19:
FI = FI Lnext
20:
L = Lnext
21:
k++
22:
Return FI
Mô tả thuật toán DFS-Apriori:
Dòng 1 và 2, sinh tập L1 chứa các item thỏa ngƣỡng minsup
và rút gọn tập giao dịch biểu diễn dạng bit (loại bỏ các giao
dịch chỉ có 1 item). Dòng 3, sinh tập phổ biến L2. Dòng 6, lọc
các 2-itemset phổ biến theo nhóm item thứ i; dòng 7 – cập
nhật vector occ theo item thứ i, đây là dạng chỉ mục trong
phép đếm độ phổ biến. Từ dòng 9 đến dòng 21, khai thác theo
chiều sâu theo item thứ i. Lặp lại dòng 5, sinh itemset phổ biến
tiếp theo item thứ i kế tiếp.
Mã giả thủ tục AprioriGenStar
Đầu vào: Tập chứa các k-itemset phổ biến Lk
Đầu ra: Tập ứng viên Ck+1
1:
Ck+1 =
2:
For (i = 1; i < |Lk| ; i++) do
3:
For (j = i+1; j |Lk| ; j++) do
4:
Ck+1 = Ck+1 {Xi Xj|{Xi Xj} Ck+1}
5:
Trả về Ck+1
Thủ tục AprioriGenNew chỉ sinh các ứng viên từ tập phổ
biến k-itemset riêng biệt nhóm theo item (chiến lƣợc tìm kiếm
theo chiều sâu) – độ phức tạp giảm đáng kể.
B. Minh họa thuật toán DFS-Apriori
Trong phần này, nhóm tác giả minh họa thuật toán DFS-
Apriori khai thác tập phổ biến trên DLGD, cho thấy thuật toán
cải tiến hiệu quả.
Theo Ví dụ 2, tập giao dịch Ƭ trong Bảng 2 và giá trị
ngƣỡng minsup = 0,30.
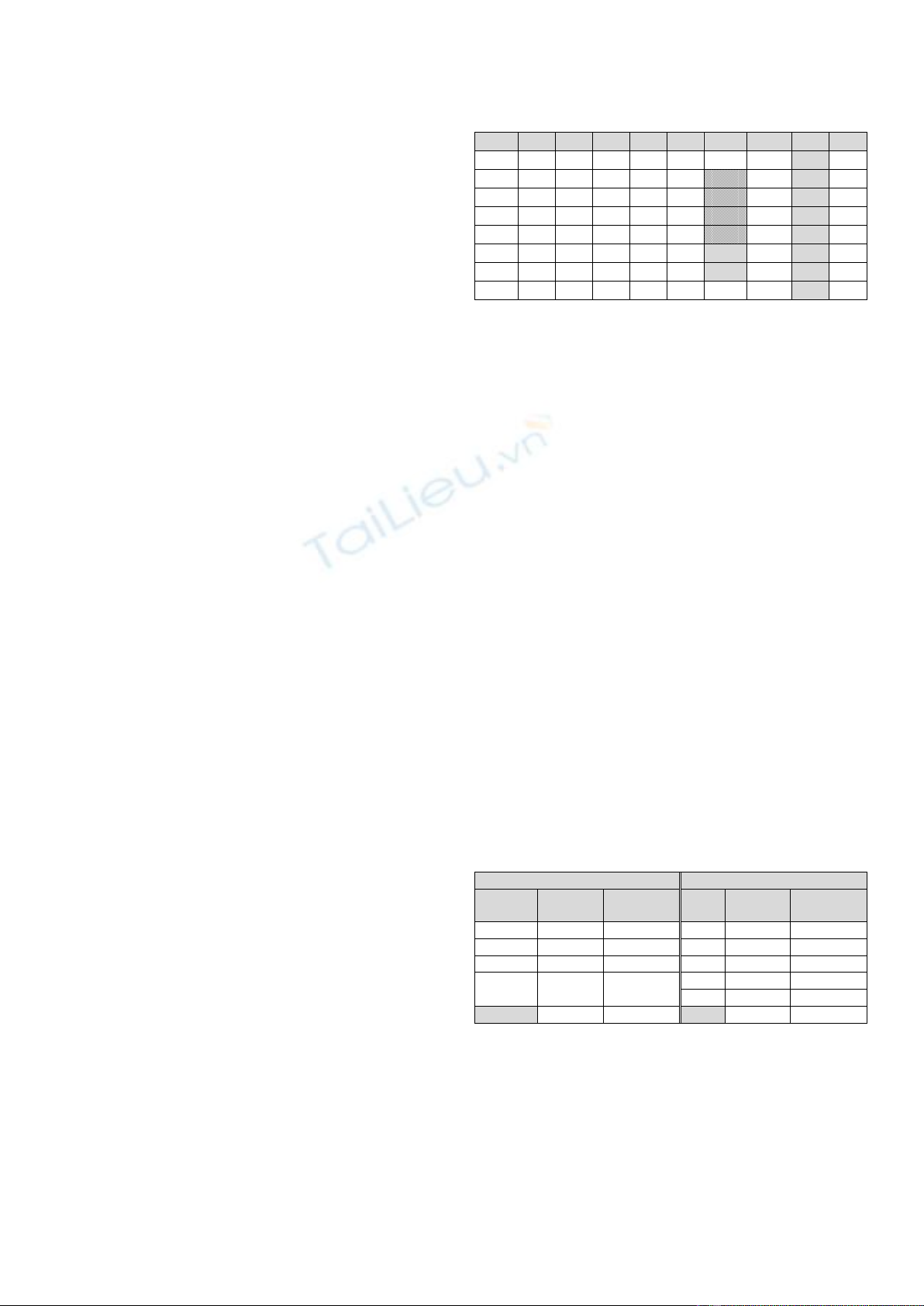
Bảng 5. Tập giao dịch T đã rút gọn – loại bỏ t3 và t6
TID
F
G
E
A
C
min
max
|t|
occ
t10
1
1
1
1
1
1
5
5
1
t1
1
0
1
1
1
1
5
4
1
t4
1
1
0
1
1
1
5
4
1
t5
0
1
1
1
1
2
5
4
0
t9
0
1
1
1
1
2
5
4
0
t2
0
1
0
1
1
2
5
3
0
t7
0
0
1
1
1
3
5
3
0
t8
0
0
0
1
1
4
5
2
0
Dữ liệu Ƭ đƣợc sắp xếp theo |t|, min, max và cột occ đƣợc
cập nhật theo vector của item F: {1, 1, 1, 0, 0, 0, 0, 0}.
Dòng 1, xét các item thỏa minsup = 0,30: có 5 items {F, G,
E, A, C} đƣợc sắp tăng dần theo độ phổ biến và gán lần lƣợt
thứ tự từ 1 đến 5;
Dòng 2, sinh tập phổ biến 1-itemset L1 = {(F; 0,30), (G;
0,50), (E; 0,70), (A; 0,80), (C; 0,80)};
Xét item F: sinh 4 ứng viên 2-itemset C2[F] = {FG, FE, FA,
FC}; tập chứa 2-itemset phổ biến L2[F] = {(FA; 0,30), (FC;
0,30)}; sinh 1 ứng viên 3-itemset C3[F] = {FAC}; tập chứa 3-
itemset phổ biến L3[F] = {(FAC; 0,30)}.
Xét item G: cập nhật vector cột occ = {1, 0, 1, 1, 1, 1, 0, 0};
sinh 3 ứng viên 2-itemset C2[G] = {GE, GA, GC}; tập chứa 2-
itemset phổ biến L2[G] = {(GE; 0,30), (GA; 0,30), (GC; 0,30)};
sinh 2 ứng viên 3-itemset C3[G] = {GEA, GEC, GAC}; tập chứa
3-itemset phổ biến L3[G] = {(GEA; 0,30), (GEC; 0,30), (GAC;
0,50)}; sinh 1 ứng viên 4-itemset C4[G] = {GEAC}; tập chứa 4-
itemset phổ biến L4[G] = {(GEAC; 0,30)}.
Xét item E: cập nhật vector cột occ = {1, 1, 0, 1, 1, 0, 1, 0};
sinh 2 ứng viên 2-itemset C2[E] = {EA, EC}; tập chứa 2-itemset
phổ biến L2[E] = {(EA; 0,50), (EC; 0,50)}; sinh 1 ứng viên 3-
itemset C3[E] = {EAC}; tập chứa 3-itemset phổ biến L3[E] =
{(EAC; 0,50)}.
Xét item A: cập nhật vector cột occ = {1, 1, 1, 1, 1, 1, 1, 1};
sinh 1 ứng viên 2-itemset C2[A] = {AC}; tập chứa 2-itemset phổ
biến L2[A] = {(AC; 0,80)}.
Kết quả khai thác tập phổ biến đƣợc trình bày ở Bảng 4
(19 itemset phổ biến: 4 itemset đƣợc khai thác theo chiều sâu
từ item F; 8 itemset từ item G; 4 itemset từ item E; 2 itemset từ
item A và 1 itemset từ item C).
C. So sánh ứng viên tiềm năng và số giao dịch duyệt của 2
thuật toán Apriori và DFS-Apriori
Bảng 6. Số ứng viên và duyệt giao dịch theo Ví dụ 2
AprioriTID
DFS-Apriori
Lần lặp k
Số
ứng viên
Số giao
dịch duyệt
Items
Số
ứng viên
Số giao
dịch duyệt
2
10
340
F
5
15
3
28
90
G
7
34
4
10
3
E
3
15
5
0
0
A
1
8
C
0
0
Tổng:
48
433
Tổng:
16
72
Bảng 6, cho thấy tổng số ứng viên tiềm năng của thuật
toán DFS-Apriori thấp hơn 66,67% so với AprioriTID và tổng
số dòng giao dịch đƣợc duyệt thấp hơn 83,37%. Qua đó, cho
thấy thuật toán DFS-Apriori khả thi và hiệu quả hơn so với
thuật toán AprioriTID.
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
138
IV. KẾT QUẢ THỰC NGHIỆM
Thực nghiệm trên máy tính Core Duo 2.0 GHz, 4GB
RAM, thuật toán cài đặt trên MSVC# 2010.
A. Mô tả dữ liệu thực nghiệm
Nghiên cứu thực nghiệm trên 2 nhóm dữ liệu:
Nhóm dữ liệu thực có mật độ dày: từ kho dữ liệu về học
máy của trƣờng Đại học California (Lichman, M. (2013).
UCI Machine Learning Repository
[http://archive.ics.uci.edu/ml]. Irvine, CA: University of
California, School of Information and Computer Science)
gồm Chess và Mushroom.
Nhóm dữ liệu giả lập có mật độ thưa: sử dụng phần
mềm phát sinh dữ liệu giả lập của trung tâm nghiên cứu
IBM Almaden (IBM Almaden Research Center, San Joe,
California 95120, U.S.A [http://www.almaden.ibm.com])
gồm T10I4D100K và T40I10D100K.
Bảng 7. Dữ liệu thực nghiệm
Dữ liệu
Số
item
Số
giao dịch
Số item trung
bình/giao dịch
Mật
độ (%)
Chess
75
3.196
37
49,3
Mushroom
119
8.142
23
19,3
T10I4D100K
870
100.000
10
1,1
T40I10D100K
942
100.000
40
4,2
Bảng 7, mô tả 4 tập dữ liệu sử dụng trong thực nghiệm,
gồm các thông số nhƣ số lƣợng các item, số lƣợng giao dịch,
số item trung bình trên mỗi giao dịch và mật độ của từng tập
dữ liệu.
B. Thực nghiệm
Để đánh giá mức độ hiệu quả của thuật toán DFS-Apriori,
chúng tôi so sánh thuật toán DFS-Apriori khai thác tập phổ
biến trên DLGD với thuật toán AprioriTID [2] đƣợc cải tiến
theo dạng bit. Cả hai thuật toán đều cho cùng kết quả trên các
ngƣỡng minsup khác nhau.
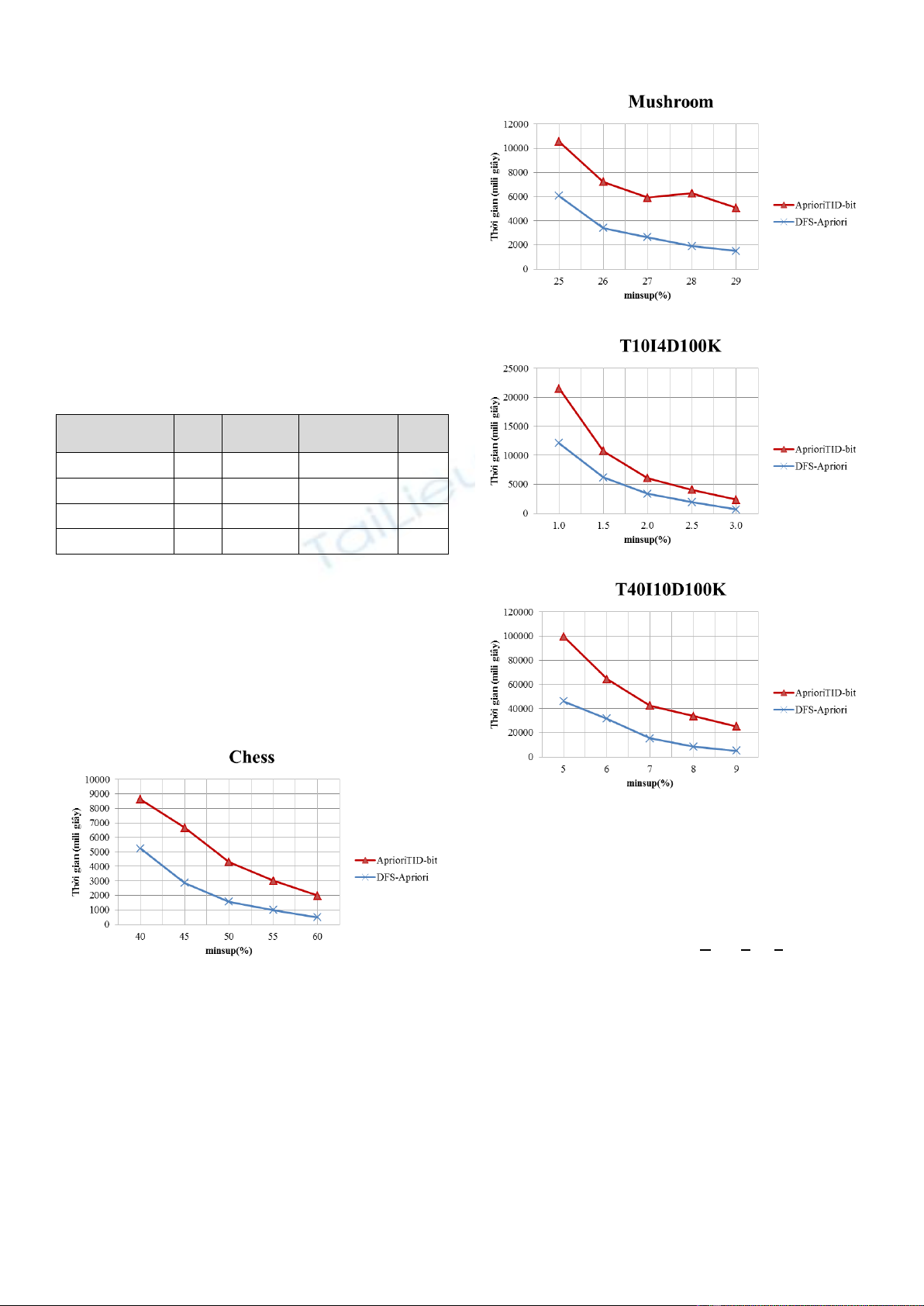
Hình 1. Thời gian thực hiện khai thác FI trên Chess
Hình 1 và 2 là kết quả thực nghiệm trên nhóm dữ liệu có
mật độ cao, ta thấy thuật toán DFS-Apriori nhanh hơn thuật
toán AprioriTID-bit.
Hình 2. Thời gian thực hiện khai thác FI trên Mushroom
Hình 3. Thời gian thực hiện khai thác FI trên T10I4D100K
Hình 4. Thời gian thực hiện khai thác FI trên T40I10D100K
Hình 3 và 4 là kết quả thực nghiệm trên nhóm dữ liệu giả
lập có mật độ thấp, ta thấy thuật toán DFS-Apriori nhanh hơn
thuật toán AprioriTID-bit. Hiệu suất của thuật toán DFS-
Apriori rất cao so với AprioriTID-bit trên dữ liệu thƣa.
Kết quả thực nghiệm, cho thấy thuật toán cải tiến DFS-
Apriori hiệu quả hơn thuật toán AprioriTID-bit. Ngoài ra, thuật
toán cũng cần thực nghiệm so sánh thêm với các thuật toán
theo hƣớng tiếp cận theo chiều sâu (Depth First Search - DFS),
cùng với nhiều tập dữ liệu khác và mở rộng trên môi trƣờng
tính toán phân tán.
V. KẾT LUẬN VÀ HƢỚNG PHÁT TRIỂN
Trong bài viết này, nhóm tác giả đề xuất tiếp cận mới trong
cải tiến hiệu quả thuật toán Apriori áp dụng chiến lƣợc tìm
kiếm theo chiều sâu: Thứ nhất, rút gọn hiệu quả không gian
sinh các ứng viên k-itemset từ tập (k-1)-itemset phổ biến; Thứ
hai, ở mỗi bƣớc tính độ phổ biến của ứng viên k-itemset chỉ
Hội nghị Quốc gia lần thứ 25 về Điện tử, Truyền thông và Công nghệ Thông tin (REV-ECIT2022)
ISBN 978-604-80-7468-5
139