21 August 2011 Hon.-Prof. Prof. Dr.-Ing. habil. Ng. Ph. Quang ĐHBK Hà Nội1
Điềukhiểnsố
(Digital Control Systems)
Các ví dụ: Đánh sốthứtựtheo
chương của giáo trình cùng tên
(Version 5, 8/2011)
21 August 2011 Hon.-Prof. Prof. Dr.-Ing. habil. Ng. Ph. Quang ĐHBK Hà Nội2
1. Mô hình tín hiệuvàhệthống
1.2 Mô hình tín hiệutrênmiềnảnh z
Ví dụ1.2.1 Một tín hiệugiánđoạnvề
thờigianđượcmôtảbởi:
()
1
1
1
1
z
Uz z
z−
==
−
−
Lờigiải:
Dễdàng tìm ảnh zcủatínhiệukểtrên bằng cách tính tổng
Laurent:
()
()
00
k
kk
kk
a
Uz az
z
∞∞
−
==
⎛⎞
⎟
⎜
==
⎟
⎜⎟
⎟
⎜
⎝⎠
∑∑
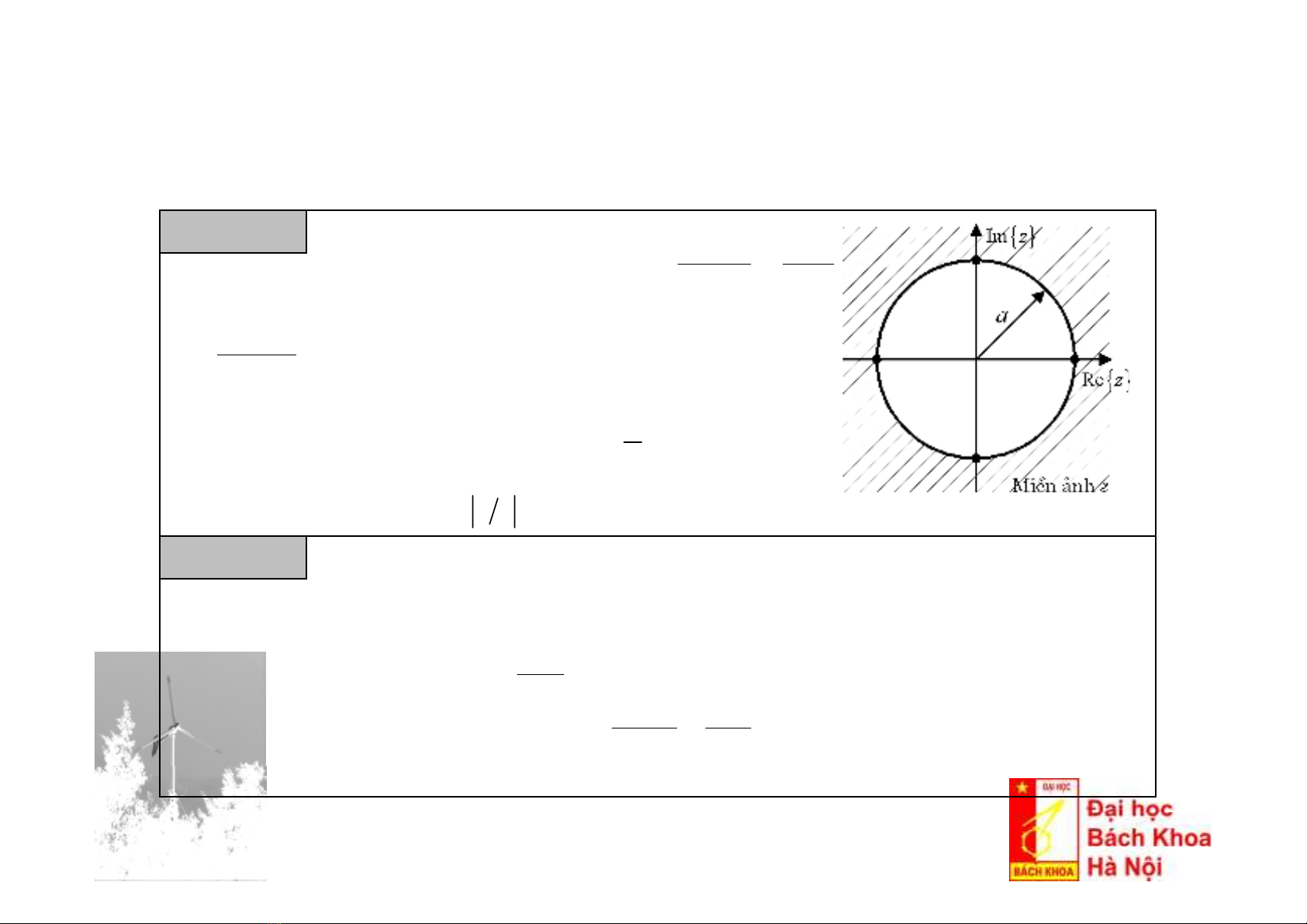
Chuỗitrênchỉhộitụkhi , tứclàởvùng phía ngoài đường tròn có bán kính a.
1az<
Hãy đi tìm ảnh U(z) và miềnhộitụcủatínhiệu!
Ví dụ1.2.2 Hãy đi tìm ảnh zcủahàm bướcnhẩyđơnvị1(t) !
() () ( )
()
1
00
1 khi 0 1 khi 0,1, 2,
11 1
0khi 0 0khi 0
k
k
k
kk
tk
ut u U z z z
tk
∞∞
−−
==
⎧⎧
≥=
⎪⎪
⎪⎪
== ⇒ = ⇒ = ⋅=
⎨⎨
⎪⎪
<<
⎪⎪
⎩⎩ ∑∑
…
()
01
s
s
r
rq q
∞
=
=−
∑
()
1
1
1
1
z
Uz z
z−
==
−
−
Kếtquảtrên đúng vớimọi giá trịtrên toàn miềnz, trừđiểmz= 1.
Khi thay vào chuỗi: các giá trịq= z-1 và r= 1 ta thu được:
21 August 2011 Hon.-Prof. Prof. Dr.-Ing. habil. Ng. Ph. Quang ĐHBK Hà Nội3
1. Mô hình tín hiệuvàhệthống
1.2 Mô hình tín hiệutrênmiềnảnh z
Ví dụ1.2.3
Ví dụ1.2.4
Hãy tìm ảnh zcủahàm e mũ(hàm exponent) !
() ( ) ( )
()
1
00
;0 ; 0,1,2, k
at akT akT k aT
k
kk
ft e t fkT f e k Fz e z e z
∞∞
−−
==
=≥⇒ == = ⇒ = =
∑∑
…
Kếtquảtính tổng củachuỗilà:
()
1
1
11
aT
aT aT
ez
Fz ez e z
−
−−
==
−−
Hãy tìm ảnh zcủahàm dốctuyến tính !
(
)
; 0; constft att a=≥=
Dễdàng viếtđượcảnh F(z) dướidạng chuỗinhưsau:
()
0
k
k
F
zakTz
∞−
=
=∑
Để tính tổng trên ta phảiáp
dụng nguyên lý tịnh tiếnvà
sửdụng ảnh zcủahàmbước
nhẩy1(t) và viếtlại công
thứctrên:
()
()
123
23
3
12 12
1
2
11 1
11 1
Tz Tz Tz
Tz Tz
Fz a Tz
zz z
aT z z aT z z
zz z
zz aTz
aT z
zz z
−−−
−−
−
−− −−
−
⎡
⎤
+++
⎢⎥
⎢⎥
++
⎢⎥
=⎢⎥
+
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎡⎤
⎡
⎤
⎢⎥
=++=++
⎢
⎥
⎣
⎦
⎢⎥
−− −
⎣⎦
==
−− −

21 August 2011 Hon.-Prof. Prof. Dr.-Ing. habil. Ng. Ph. Quang ĐHBK Hà Nội4
1. Mô hình tín hiệuvàhệthống
1.2 Mô hình tín hiệutrênmiềnảnh z
Ví dụ1.2.5
Bổxung lý thuyết:
Tìm hàm gốccủaảnh zcho trướcbằng phương pháp tách phân thứchữutỷthành
các phân thứctốigiản. Sau đólầnlượt tìm hàm gốccủa các phân thứctốigiản.
k
za
za⇔
−
()
()
1;1,2,
1
1
1
km
m
mkm
k
zam
m
za
k
za a
m
−+
−−
⎛⎞
⎟
⎜⎟
⇔=
⎜⎟
⎜⎟
⎜⎟
−
⎝⎠
−
⎛⎞
−⎟
⎜⎟
−⇔
⎜⎟
⎜⎟
⎜⎟
−
⎝⎠
•Điểmcựcđơn: •Điểmcựclặplạimlần:
Cho trướcảnh zcó dạng phân thức:
()
2
0,9
0,5 0, 4
0,1 0, 2
z
zz
Fz zz
zz
==−
−+
−−
Áp dụng công thứcđể tìm hàm gốc:
)
0,5 0, 4 k
k
k
f=−−
Ví dụ:
21 August 2011 Hon.-Prof. Prof. Dr.-Ing. habil. Ng. Ph. Quang ĐHBK Hà Nội5
1. Mô hình tín hiệuvàhệthống
1.2 Mô hình tín hiệutrênmiềnảnh z
()
(
)
(
)
0,9
0,5 0, 4
z
Fz zz
=−+
Xét hàm ảnh cho ởví dụ1.2.5:
() ()
()()
() ()
()()
()
1
2
1
1
10,5
z
1
1
20,4
z
0,9 0,5
0,5 Res lim 0,5
0,5 0, 4
0,9 0, 4
0, 4 Res lim 0, 4
0,5 0, 4
k
kk
z
k
k
k
z
zz z
zFzz
zz
zz z
zFzz
zz
−
−
→
−
−
→−
⎧
⎡
⎤
⎪−
⎪⎢⎥
⎡⎤
⎪=⇒ = =
⎪⎢⎥
⎢⎥
⎣⎦
⎪−+
⎢⎥
⎪⎣⎦
⎪
⎪
⎨
⎪⎡⎤
+
⎪⎢⎥
⎪⎡⎤
=− ⇒ = =− −
⎪⎢⎥
⎢⎥
⎣⎦
⎪−+
⎪⎢⎥
⎣
⎦
⎪
⎩
⎪
Có hai điểmcựcz1, z2, vậykhi:
Hàm gốccódạng sau:
(
)
0,5 0, 4 k
k
k
f=−−
Ví dụ1.2.6 Bổxung lý thuyết:Tìm hàm gốccủaảnh zcho trướcbằng phương pháp tính
Residuum. Khi z= zνlà điểmcực
-lặplạimlần:
-đơn:
Hàm gốccódạng:
()
1
1
Res
n
k
k
f
Fzz
ν
−
=
⎡⎤
=⎢⎥
⎣⎦
∑
() () ()( )
() ()( )
1
11
1
z
11
z
1
Res lim
1!
Res lim
mm
kk
m
zz
kk
zz
d
Fzz Fz z z z
mdz
Fzz Fz z z z
ν
ν
ν
ν
ν
ν
−
−−
−
→
−−
→
⎡
⎤
⎡⎤
=−
⎢
⎥
⎢⎥
⎣⎦
⎣
⎦
−
⎡⎤⎡ ⎤
=−
⎢⎥⎢ ⎥
⎣⎦⎣ ⎦