131
CH NG TÁM 8
PHÂN TÍCH VÀ DI N GI I D LI U
TRONG NGHIÊN C U MARKETING
N I DUNG CHÍNH
N i dung ch ng này bàn n bao g m:
-Th nào là gi thuy t nghiên c u
-Các lo i sai l m khi th c hi n ki m nh gi thuy t
-Các b c gi i quy t m t bài toán ki m nh
-Các ph ng pháp ki m nh tham s
-Các ph ng pháp ki m nh phi tham s
MÔ HÌNH L A CH N PH NG PHÁP KI M NH
Gi thi t th ng kê là m t gi thi t có liên quan n m t trong ba v n sau:
(1) Tính c l p hay ph thu c c a i l ng ng u nhiên c n nghiên c u.
(2) D ng c a qui lu t phân ph i xác su t c a i l ng ng u nhiên.
(3) Giá tr c a tham s c a qui lu t phân ph i xác su t ã bi t d ng.
(1) & (2) là gi thi t phi tham s và (3) là gi thi t v tham s .
Trong ph n này s gi i thi u ph ng pháp ki m nh gi thi t v tham s nh tham s trung bình
x trong qui lu t phân ph i chu n N( , 2), tham s t l p trong qui lu t phân ph i A(P), tham s
chi bình ph ng, tham s Fisher Trong khuôn kh cu n sách này, chúng tôi ch gi i thi u cách
th c áp d ng nh ng ph ng pháp ki m nh ó gi i quy t nh ng v n liên quan n nghiên
cu ti p th , nh ng v n khác liên quan n vi c gi i thích b n ch t c a các công th c có th
tham kh o thêm trong các giáo trình chuyên môn v th ng kê toán.
Các khái ni m c b n
Gi thi t c n ki m nh
Gi s i l ng ng u nhiên X c n nghiên c u tuân theo m t qui lu t phân ph i xác su t ã bi t
dng, nh ng ch a bi t giá tr c a tham s nào ó c a nó. Trên c s nh ng tin t c thu c, ta
có th gi nh r ng = 0, trong ó0 là s th c. T t nhiên i u gi nh = 0 này có th úng
ho c có th sai, do ó c n ph i ki m tra l i gi nh ó. T ó ta có gi thi t c n ki m nh là
{ H0: = 0} .
Các gi thi t i ( i thi t)
Vì gi thi t H0 c ng có th úng và c ng có th sai v i m t tin c y nào ó, khi gi thi t H0 sai
thì ta ph i bác b nó. Khi ó ph i ch p nh n m t trong ba gi thi t i (ký hi u: H1) sau ây:
-Trong tr ng h p ki m nh d ng "hai uôi" (Two-tail test):
01
00
:H
:
H
-Trong tr ng h p ki m nh d ng "m t uôi" (One-tail test):
01
00
:H
:Hho c
01
00
:H
:H
Do v y trong bài toán ki m nh gi thi t, sau khi ã ra gi thi t c n ki m nh H0, ta c n phát
bi u kèm m t gi thi t i H1 kh ng nh r ng n u nh gi thi t H0 b bác b thì ta ch p nh n
gi thi t i kèm theo v i m t m c ý ngh a nào y (1- c g i là tin c y).
Các lo i sai l m
Chú ý r ng, vì m u không ph i là hình nh chính xác c a t ng th , nên m i m u ch n c u
ch a m t sai s ng u nhiên nào ó. Do v y, khi d a vào m u ki m nh gi thi t có th g p
ph i hai lo i sai l m sau:
-Sai l m lo i 1: Khi ta bác b m t gi thi t úng.
-Sai l m lo i 2: Khi ta th a nh n m t gi thi t sai.
132
Trong khi ti n hành ki m nh, ng i ta th ng n nh tr c m t xác su t m c sai l m lo i 1.
Nu xác su t này b ng , thì c g i là m c ý ngh a c a ki m nh (thông th ng ph i khá
bé, = 0,05, = 0,1).
Gi thi t H0úng Gi thi t H0 sai
Ch p nh n Quy t nh úng Sai l m lo i 2 (xác su t )
Bác b Sai l m lo i 1 (xác su t ) Quy t nh úng
Tiêu chu n ki m nh và mi n bác b
Sau khi ã ra gi thuy t H0 c n ki m nh kèm theo gi thi t i H1 và qui nh m c ý ngh a
, ta c n ph i tìm m t th ng kê T cùng qui lu t phân ph i xác su t c a nó. V i m t m c ý ngh a
xác nh, ta luôn tìm c m i mi n W , th a mãn i u ki n 0
HWKP (xác su t
K thu c mi n mi n bác b W v i i u ki n H0úng b ng ).
Do khá bé, nên ta có th coi bi n c (K W ) là bi n c không th có (v i i u ki n gi thi t H0
úng). Vì v y, trong th c t n u d a vào giá tr x c a m u ng u nhiên X, ta tính c giá tr kqs
ca th ng kê K mà l i th y giá tr kqs W , thì i u này s mâu thu n v i i u ki n nói trên.
Nguyên nhân sinh ra mâu thu n gi a lý thuy t và th c t là do ta gi thi t r ng H0úng. tránh
mâu thu n này ta ph i bác b gi thi t, vì th W c g i là mi n bác b và kqs c g i là tiêu
chu n ki m nh.
Chú ý:
-Khi gi thi t H0úng thì tiêu chu n ki m nh K v n có th nh n giá tr kqs W v i xác su t
xy ra là . Vì v y trong tr ng h p kqs W mà ta bác b gi thi t H0 thì ta có th m c sai
lm lo i 1, v i xác su t m c sai l m lo i 1 chính là .
-Nu ta ký hi u 1
HWkP qs thì là xác su t bác b m t gi thi t sai. Do ó, xác su t
không bác b m t gi thi t sai 1
1
HWKP qs là xác su t m c sai l m lo i 2 và s
c g i là xác su t không m c sai l m lo i 2, ng i ta g i là hi u l c c a ki m nh.
-Vi kích th c m u n xác nh thì v i m u tiêu chu n ki m nh ta s có mi n bác b W th a
mãn i u ki n: 0
HWKP qs .
Nu t n t i m t tiêu chu n ki m nh kqs v i mi n bác b W sao cho (1- ) là nh nh t và l n
nh t. Khi ó kqs c g i là tiêu chu n ki m nh m nh nh t. M t tiêu chu n c coi là m nh
nh t thì nó m b o 3 yêu c u:
-Xác su t m c sai l m lo i 1 là qui nh tr c.
-Xác su t m c sai l m lo i 2 là nh nh t.
-Khi bác b gi thi t H0 thì ta có th th a nh n gi thi t i H1.
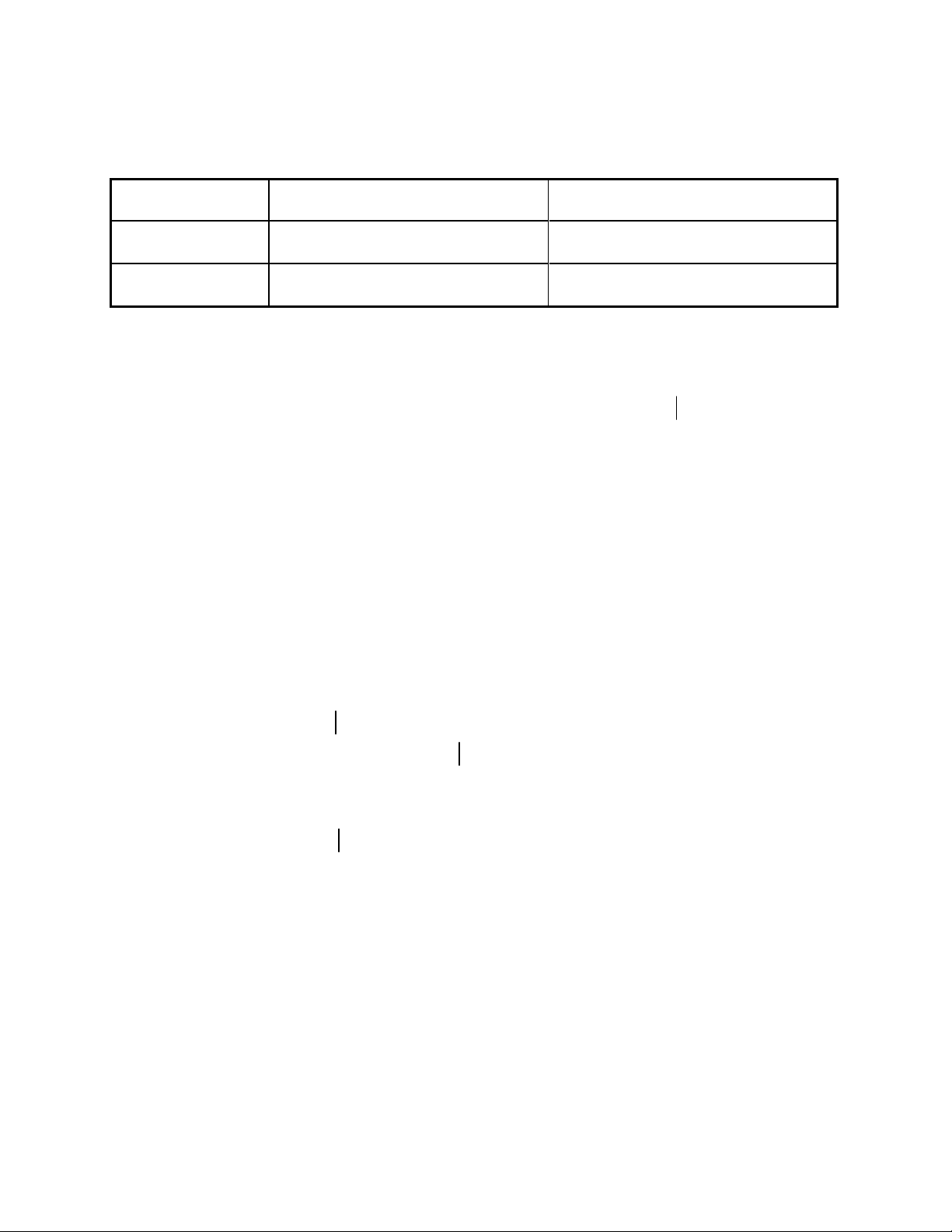
Nh v y chúng ta có th xác nh mi n bác b và mi n ch p nh n trong các tr ng h p ki m
nh m t uôi và hai uôi là:
-Trong ki m nh hai uôi:
133
134
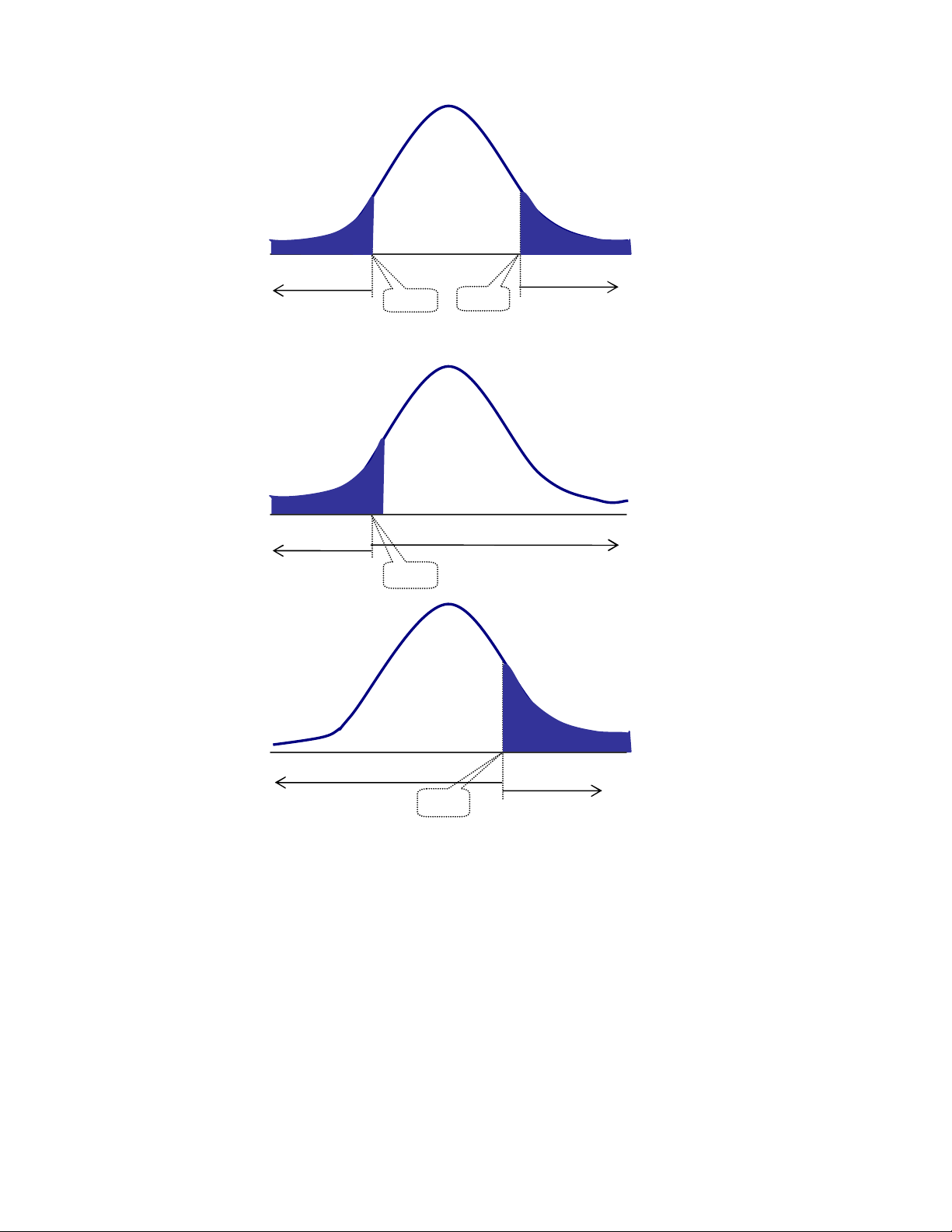
-Trong ki m nh m t uôi:
Các b c chung gi i bài toán ki m nh
Bc 1: Phát bi u gi thi t và i thi t
01
00
:H
:
Hho c ho c
01
00
:H
:
H
01
00
:H
:
H
Bc 2: Xác nh m c ý ngh a và xây d ng mi n bác b
+ M c ý ngh a
+ Mi n bác b (tùy thu c vào ph ng pháp ki m nh, lo i phân ph i và m c ý ngh a).
Bc 2: L a ch n ph ng pháp ki m nh và lo i phân ph i c a nó.
B c 4: Tính giá tr quan sát c a tiêu chu n ki m nh kqs
Bc 5: So sánh v i mi n bác b k t lu n:
Mi n bác b
Mi n ch p nh n
W1-
Mi n bác b Mi n ch p nh n
-W1-
Mi n bác b Mi n bác b
Mi n ch p nh n
W1- /2-W1- /2