
SÁNG KIẾN KINH NGHIỆM
KINH NGHIỆM DẠY PHẦN SO
SÁNH PHÂN SỐ Ở MÔN TOÁN 6

I. Đặt vấn đề
Toán là môn học cơ bản trong chương trình phổ thông nói chung và trong
chương trình THCS nói riêng. Học toán hay giải bài toán là yêu cầu thường
xuyên trong mọi hoạt động và suy nghĩ. Do đó, trong quá trình dạy học toán
nói chung cũng như trong quá trình dạy giải toán số học nói riêng, người dạy
học và người học cần phải tạo ra cho mình một thói quen là : Sau khi học xong
lí thuyết cần phải nắm chắc kiến thức cơ bản từ đó vận dụng sáng tạo, có hiệu
quả vào bài toán, tìm được lời giải của bài toán đó rồi dù là đơn giản hay phức
tạp cần suy nghĩ, kiểm tra lí thuyết, lật lại vấn đề xem có cách nào cho ta kết
quả hay hơn, tìm được cái mới hơn rồi lại đi tìm cái mới hơn nữa, cứ thế
chúng ta sẽ tìm ra được những điều thú vị.
Là một người trực tiếp chỉ đạo về công tác chuyên môn tôi nghĩ làm thế
nào để tổ chức các chuyên đề cho giáo viên, để giáo viên truyền lại cho học
sinh nắm được bài, hiểu bài và biết vận dụng để từ đó giải được các bài tập từ
đơn giản đến phức tạp và có kết quả cao trong các kỳ thi. Chính vì vậy tôi đã
tìm tòi, đọc tài liệu tham khảo … để cùng với các giáo viên khác làm cho học
sinh biết vận dụng sáng tạo, có hiệu quả “phương pháp so sánh phân số” vào
các bài toán so sánh phân số. Loại toán này quen thuộc đối với học sinh lớp 6.
Đó là điều băn khoăn trăn trở đối với tôi trong quá trình chỉ đạo và giảng dạy.
Từ đó tôi nghĩ đến việc vận dụng sáng tạo lí thuyết các phương pháp so sánh
phân số vào các bài toán có liên quan đến so sánh phân số mà hiện nay học
sinh đang nghèo nàn về phương pháp. Bài viết này tôi xin đưa ra một số
phương pháp so sánh phân số. Đó là điều băn khoăn trăn trở đối với tôi trong
quá trình chỉ đạo và giảng dạy. Từ đó tôi nghĩ đến việc vận dụng sáng tạo lí
thuyết các phương pháp so sánh phân số vào các bài toán có liên quan đến so
sánh phân số mà hiện nay học sinh đang nghèo nàn về phương pháp. Bài viết
này tôi xin đưa ra một số phương pháp so sánh phân số.
II. Giải quyết vấn đề.
Tóm tắt lí thuyết các phương pháp so sánh phân số.
(Trong tập hợp Q+) quen thuộc là :
1. Quy đồng các phân số đã cho rồi so sánh các tử số với nhau
2. Viết các phân số đã cho dưới dạng các phân số cùng tử số rồi so sánh các
mẫu với nhau.
3. So sánh phân số theo tính chất: nếu ad < bc thì d
c
b
a
4. So sánh tỉ số các phân số đã cho với 1 theo tính chất : Nếu x : y <1 thì x < y
(y ≠ 0)
5. Viết các phân số dưới dạng số thập phân rồi so sánh các số thập phân.
6. So sánh các số nghịch đảo của các phân số theo tính chất : Cho a,b,c d ≠ 0,
nếu c
d
a
bthì d
c
b
a

7. Dựa vào tính chất bắc cầu của quan hệ thứ tự : Nếu n
m
b
a và d
c
n
m thì
d
c
b
a
8. So sánh “phần bù của một phân số đối với đơn vị” theo tính chất nếu
1;
d
c
b
a và d
c
b
a 11 thì d
c
b
a
Tiếp theo tôi xin nêu thêm vài cách so sánh khác :
9. Ta có tính chất.
Nếu d
c
b
a thì d
c
db
ca
b
a
Chứng minh :
Từ d
c
b
a => ad < bc
ad + ab < bc + ab => a(b+d) < b(a+c)
db
ca
b
a
(1)
d
c
b
a => ad < bc => ad + dc < bc + dc
d(a+c) < c(b+d) => d
c
db
ca
(2)
Từ (1) và (2) => b
a<d
c
db
ca
(đpcm)
10. Từ tính chất đã nêu ở cách 9 ta dễ dàng suy ra tính chất sau : Nếu d
c
b
a
thì b
a<d
c
dbn
can
(n = 1,2,3…)
Chứng minh :
Từ d
c
b
a => ad <bc
ad + abn < bc + abn => a(d+bn) < b (c+an)
bnd
anc
b
a
(1)
Lại có từ : d
c
b
a => ad<bc
adn < bcn => adn + dc < bcn + dc
d(an+c) < c(bn+d)
d
c
dbn
can
(2)
Từ (1) và (2) => b
a
<d
c
dbn
can
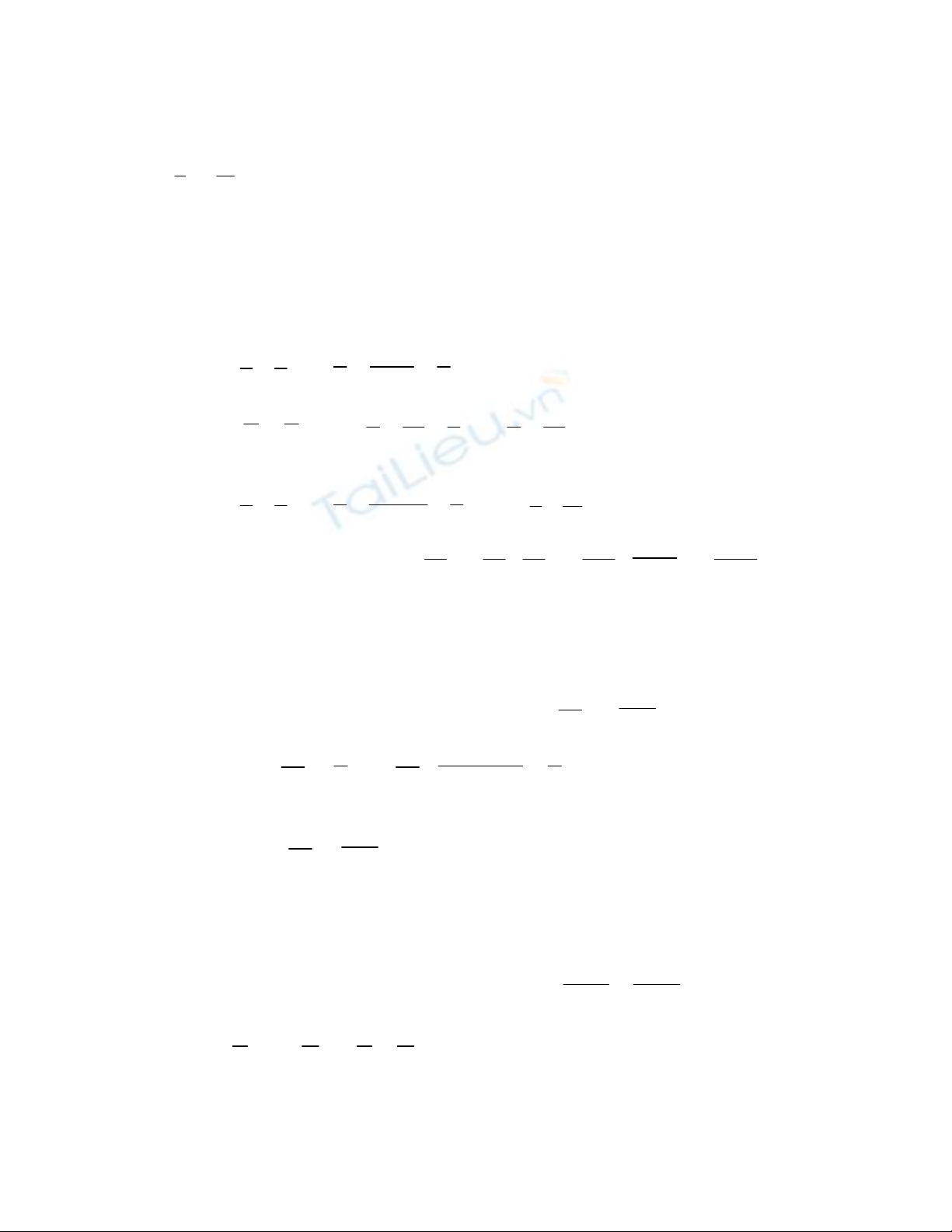
Xin giới thiệu một số ví dụ .
Bài 1: So sánh bằng nhiều phương pháp khác nhau. Xem trong hai phân số
7
5và 16
13 thì phân số nào lớn hơn.
Đây là một bài toán đơn giản nhưng chứa đựng nhiều vấn đề trong
chương trình toán 6.
Ở bài toán này do 4 số 5,7,13,16 đôi một nguyên tố cùng nhau. Nên khi
áp dụng các cách giải 1,2,3,4 vào bài toán trên ta đều qui về so sánh 5,16
và 7,13 .
Vận dụng cách thứ 9 ta làm như sau :
Vì 3
2
7
5 nên 3
2
27
35
7
5
Từ 9
8
7
5 suy ra 9
8
16
13
7
5 vậy 16
13
7
5
Hoặc vận dụng cách thứ 10 ta làm như sau :
Vì 3
2
7
5 nên 3
2
22.7
32.5
7
5
suy ra 16
13
7
5
Ví dụ 2: So sánh các phân số 82
35 và 83
36 ; 99
97 và 991
969 ; 2010
2006 và 2013
2009
Khi so sánh các phân số trên rõ ràng ta nên áp dụng các cách 6,7,8 tương
ứng là hợp lý nhất.
+ Để vận dụng cách thứ 10 vào ví dụ 1 ta cần viết :
13 = 5.2 + 3 ; 16 = 7.2 + 2
Tương tự chẳng hạn ta so sánh 2 phân só sau : 95
89 và 954
895
Ta có 95
89 < 4
5 nên 95
89 <410.95
510.89
< 4
5
Do đó 95
89 < 954
895
* Một điều thú vị là nhờ so sánh các phân số mà ta có một cách chứng minh
tính chất sau :
Cho a , b , c, d N , nếu a < b
c < d và a + d = b + c thì ad < bc
Thật vậy từ giả thiết suy ra
db
dcba
0 => d
cd
b
ab
=> bcad
d
c
b
a
d
c
b
a 11
Nghĩa là : Cho hai số tự nhiên biến thiên có tổng không đổi, thế thì tích của
chúng càng lớn nếu hiệu của chúng càng nhỏ.
Ví dụ : 95.98 > 94.99

a2 > (a-1)(a+1) (1)
Thật ra tính chất này cũng đúng với a,b,c, d
Q+
Khi đó ta xét các tỉ số tương ứng thay cho phân số, rõ ràng bài toán đơn gian
nhưng cũng chứa nhiều vấn đề lý thú
Sau đây ta xét tiếp một số ví dụ:
Ví dụ 3:
a. So sánh các phân số theo cách hợp lí nhất:
96
47
và 100
49
Ta có:
100
49
96
47
100
49
496
247
4
2
96
47
b. 91
18 và 14
23
Hướng dẫn: 114
23
115
23
5
1
90
18
91
18
c. 523
310
1
523
213
;
520
310
1
520
210
52
21
Ta có: 523
310
520
310 Nên 523
213
52
21
d. 9191
1313 và 7
1
7373
1111
Hướng dẫn: 7373
1111
73
11
77
11
7
1
91
13
9191
1313
e. 3n
nvà )(
36
13 Nn
n
n
Hướng dẫn: 36
13
36
3
12
n
n
n
n
n
n
g. 810
510
7
7
và 710
610
8
8
Hướng dẫn: 810
13
1
810
510
77
7
Và 710
13
1
710
610
88
8
Do 710
13
810
13
87
Nên 710
610
810
510
8
8
7
7
f. 110
110
2009
2010
A và 110
110
2010
2011
B


























