Chương 3: Các phép biến đổi thuần nhất
35
Chương 3
CÁC PHÉP BIẾN ĐỔI THUẦN NHẤT
Ở chương 2, chúng ta đã tìm hiểu các kiến thức cơ bản về các hệ cân bằng
lực cũng như động học của cánh tay máy. Đối với các robot có kết cấu đơn
giản, chúng ta có thể áp dụng các phương thức trực tiếp về lực, momen và các
thành phần động học để phân tích động học cho robot công nghiệp. Tuy nhiên,
phương pháp này gặp nhiều khó khăn đối với các bài toán của robot có cấu
hình phức tạp. Vì vậy, trong chương này chúng ta tìm hiểu cách thức tiếp cận
khác trong vấn đề giải quyết bài toán động học robot, đó là các phép biến đổi
trong hệ toạ độ thuần nhất (gọi tắt là các phép biến đổi thuần nhất). Phương
pháp này là bước phát triển từ các nền tảng toán học, cơ học đã tìm hiểu ở
chương trước.
3.1. Hệ toạ độ thuần nhất.
Để biểu diễn 1 điểm trong không gian 3 chiều, người ta dùng vector điểm (
Point Vector)
Các vector điểm thường được kí hiệu bằng các chữ viết thường. Ví dụ
pva ,,
…
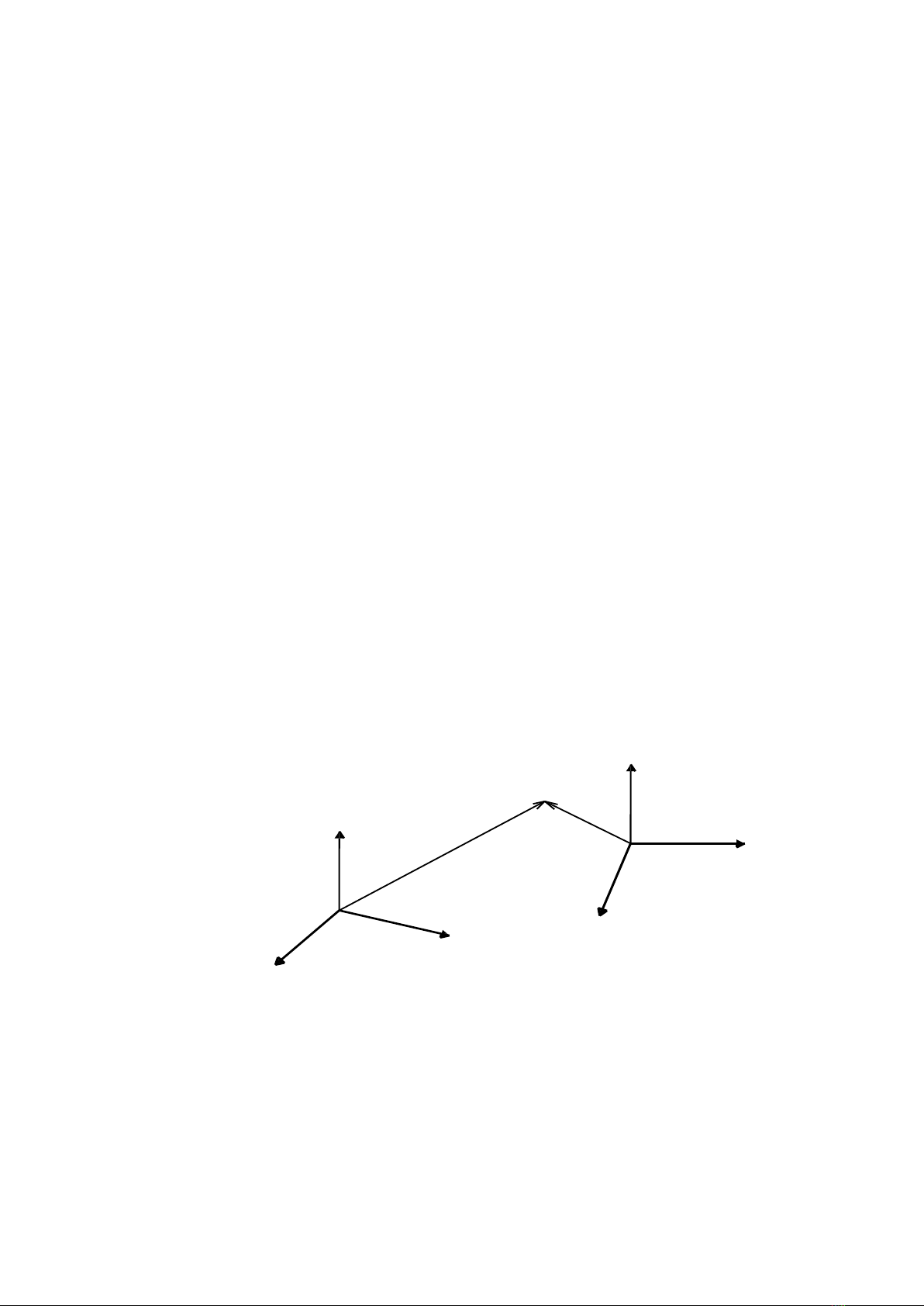
Tuỳ thuộc hệ qui chiếu được chọn mà 1 điểm trong không gian có thể được
biểu diễn bằng các vector điểm khác nhau
Ví dụ :
A
xA
yÂ
zAB
xC
yC
zC
V
VB
VA
Nếu gọi
kji
,,
là các vector định vị của hệ toạ dộ nào đó thì vector điểm
v
:
kcjbiav
Với a,b,c là toạ độ vị trí của điểm v.
o Nếu quan tâm đồng thời vấn đề vị trí và định hướng ta phải biểu diễn vector
điểm
v
trong không gian 4 chiều :
Chương 3: Các phép biến đổi thuần nhất
36
w
z
y
x
v
, với
;
b
w
y
;
c
w
z
Với w là hằng số thực (hằng số tỉ lệ).
+ Khi w=1 thì x=a; y=b; z=c : Hệ toạ độ thuần nhất (Lúc này toạ độ không gian
4 chiều trùng với toạ độ không gian 3 chiều)
+ Khi w=0 thì x, y, z →∞ : Thể hiện hướng của các trục toạ độ
→ Sử dụng hệ toạ độ với w=0 và w=1 thì có thể thể hiện cả vị trí và định hướng
vật thể.
+ Ki w≠0, và w≠0 thì :
kcjbiav
Ví dụ :
kjiv
32
o Các trường hợp đặc biệt :
+ [0, ,0, 0, 0]T : Vector không xác định.
+ [0, 0, 0, n]T : Vector 0.
+ [x, y, z, 0]T : Vector chỉ hướng.
+ [x, y, z, 1]T : Vector trong hệ toạ độ thuần nhất.
3.2. Nhắc lại các phép tính về vector và ma trận.
3.2.1) Phép nhân vector :
Cho 2 vector :
kajaiaa zyx
kbjbibb zyx
a. Tích vô hướng 2 vector :
zzyyxx babababa
.
b. Tích có hướng hai vector (Tích hai vector) :
zyx
zyx
bbb
aaa
kji
cba
.
3.2.2. Các phép tính về ma trận :
a. Phép cộng trừ hai ma trận :
Điều kiện : Các ma trận phải cùng bậc (cùng kích thước)
Chương 3: Các phép biến đổi thuần nhất
37
Cộng (trừ) hai ma trận A,B cùng bậc ta có ma trận C cùng bậc với các phần tử
ijijij BAC
b. Tích hai ma trận :
Điều kiện : Số cột của ma trận thứ nhất bằng số hàng của ma trận thứ hai.
Tích của hai ma trận A(m,n) với ma trận B(n,p) là ma trận C(m,p).
Ví dụ :
987
654
321
A
và
6
4
2
5
3
1
B
100
64
28
76
49
22
.CBA
Chú ý :
+ A.B ≠ B.A
+ (k.A).B = k.(A.B) = A.(k.B)
+ A.(B.C) = (A.B).C
+ (A+B).C = A.C+B.C
+ C.(A+B) = C.A+C.B
c. Ma trận nghịch đảo :
IAA
1
.
Điều kiện : Ma trận A là khả đảo (det(A) ≠ 0)
Có một số cách để tính ma trận nghịch đảo. Một trong số đó :
+ Tính định thức : det(A)
+ Tính ma trận C là ma trận phần phụ đại số của ma trận A :
ij
ji
ij DC
)1(
với
)det( ijij MD
+ Tính ma trận nghịch đảo theo :
T
C
A
A)det(
1
1
d. Ma trận nghịch đảo của ma trận thuần nhất :
Cho ma trận thuần nhất A :
Chương 3: Các phép biến đổi thuần nhất
38
1000
zzzz
yyyy
xxxx
paon
paon
paon
A
paonA
Tìm ma trận nghịch đảo của ma trận thuần nhất :
1000
.
.
.
paaaa
poooo
pnnnn
A
zyx
zyx
zyx
Ví dụ : Cho
1000
3001
2010
1100
A
1000
1001
2010
3100
1
A
Kiểm tra :
IAA
1000
0100
0010
0001
.1
e. Vết của ma trận :
Vết của ma trận vuông bậc n là tổng các phần tử trên đường chéo chính.
Kí hiệu :
n
i
ii
aATrATrace
1
)()(
f. Đạo hàm và tích phân của ma trận :
Nếu các phần tử của ma trận A là hàm nhiều biến thì các phần tử của ma
trận đạo hàm bằng đạo hàm riêng của các phần tử ma trận A theo biến tương
ứng.
Chương 3: Các phép biến đổi thuần nhất
39
khg
fed
cba
A
t
k
t
h
t
g
t
f
t
e
t
d
t
c
t
b
t
a
A
Tương tự cho phép tích phân ma trận.
3.3. Các phép biến đổi ma trận dùng trong động học robot.
Cho
u
là vector biểu diễn điểm cần biến đổi
h
là vector dẫn được biểu diễn b ma trận H là ma trận chuyển đổi :
uHv .
Là vector biểu diễn điểm sau khi chuyển đổi.
3.3.1. Phép biến đổi tịnh tiến.
Giả sử cần tịnh tiến 1 điểm hay hay 1 vật thể theo vector dẫn :
kcjbiah
...
Ma trận chuyển đổi tịnh tiến theo vector dẫn :
1000
100
010
001
c
b
a
H
Gọi
u
là vector biểu diễn điểm cần tịnh tiến :
u= [x, y, z, 1]T
111000
100
010
001
.cz
by
ax
z
y
x
c
b
a
uHv
Kí hiệu : v= Trans(a,b,c).u
Ví dụ : Cho
kjiu
.2.3.2
kjih
.7.3.4