Chương 5: Động lực học robot và ứng dụng trong điều khiển
64
Chương 5
ĐỘNG LỰC HỌC ROBOT VÀ ỨNG DỤNG
TRONG ĐIỀU KHIỂN
5.1. Mục đích và phương pháp khảo sát động lực học robot
Với những mục đích thiết kế và điều khiển, cần thiết phải có một mô hình
toán học mô tả động lực học của hệ thống. Vì thế, ở chương này ta sẽ xác lập
phương trình chuyển động của tay máy dưới dạng phương trình vi phân. Phương
pháp áp dụng ở đây là xây dựng phương trình chuyển động của cơ hệ dựa trên
quan hệ năng lượng, xuất phát từ nguyên lý bảo toàn và chuyển hóa năng lượng
trên cơ sở xác lập quan hệ giữa động năng và thế năng của cơ hệ tay máy, sau đó
sử dụng phương trình vi phân của chuyển động trên cơ hệ với các đại lượng
tham gia vào phương trình gồm lực, quán tính và năng lượng.
Việc nghiên cứu động lực học Robot thường giải quyết hai nhiệm vụ sau :
1. Xác định momen và lực động trong quá trình chuyển động. Khi đó qui luật
biến đổi của biến khớp qi(t) xem như đã biết.
Việc tính toán lực cũng như momen trong cơ cấu tay máy là nhiệm vụ tất
yếu trong việc lựa chọn công suất động cơ, tính toán kiểm tra độ bền, độ cứng
vững, đảm bảo độ tin cậy cho Robot.
2. Xác định các sai số động, tức là sai số xuất hiện so với qui luật chuyển động
trong chương trình.
Có nhiều phương pháp nghiên cứu động lực học Robot, nhưng nhiều hơn
cả là phương pháp cơ học Lagrange, cụ thể là phương trình Lagrange-Euler.
Trong phạm vi nội dung của môn học này, chúng ta tìm hiểu nhiệm vụ thứ
nhất, từ đó tạo cơ sở cho việc lập trình và điều khiển robot.
5.2. Động lực học robot với phương trình Euler-Lagrange.
Hàm Lagrange của một hệ thống năng lượng được định nghĩa :
L= K – P
Trong đó : K là tổng động năng của cơ hệ
L là tổng thế năng của cơ hệ
K và P đều là những đại lượng vô hướng, nên có thể chọn bất kỳ hệ tọa độ
nào để giả bài toán đơn giản.
Xét một Robot có n khâu thì :
Chương 5: Động lực học robot và ứng dụng trong điều khiển
65
n
i
i
KK
1
và
n
i
i
PP
1
(2.1)
Trong đó, Ki và Pi là động năng và thế năng của khâu thứ i xét trong hệ tọa
độ đã chọn. Đó là các đại lượng phụ thuộc vào nhiều biến số :
iii qqKK
,
và
iii qqPP
,
(2.2)
Với qi là tọa độ suy rộng của khớp thứ i.
Định nghĩa : Lực (hay momen) tổng quát tác dụng lên khâu thứ i được xác
định bởi phương trình Lagrange :
qq
LL
dt
d
F
5.3. Khảo sát bài toán động lực học của tay máy nhiều bậc tự do
Phương trình chuyển động Lagrange thiết lập cho một cơ hệ được cho bởi:
τ
qq
LL
dt
d
(2.3)
Trong đó q là vectơ biểu diễn các toạ độ suy rộng của các khâu của Tay
máy qi,
là vectơ biểu diễn các lực suy rộng của các khâu của tay máy và hàm
Lagrange là sự chênh lệch giữa động năng và thế năng của cơ hệ :
(2.4)
a. Ví dụ 1.
Ta xét ví dụ xây dựng phương trình chuyển động của tay máy hai khâu phẳng
liên kết bằng khớp bản lề.
Trong ví dụ này, ta áp dụng các kết quả của bài toán động học đã được khảo
sát ở phần trước. Để xây dựng bài toán động lực học, ta khảo sát cơ hệ với giả
thiết rằng khối lượng của khâu được tập trung ở các khớp. Ma trận biến khớp là:
T
q21
(2.5)
và ma trận biểu diễn của lực suy rộng được thể hiện:
T
21
(2.6)
với
21,
là các mô men được cho bởi các cơ cấu tác động (chẳng hạn là mô
men phát động của các động cơ điện).
Chương 5: Động lực học robot và ứng dụng trong điều khiển
66
Hình 5.1: Tay máy hai khâu bản lề
Biểu thức động năng và thế năng
Với khâu 1, ta có biểu thức của động năng và thế năng tương ứng là:
2
1
2
11
2
1
1
amK
(2.7)
1111 sin
gamP
(2.8)
Với khâu 2 ta có:
)cos(cos 212112
aax
(2.9)
)sin(sin 212112
aay
(2.10)
)sin()(sin 212121112
aax
(2.11)
)cos()(cos
212121112
aay
(2.12)
Bình phương vận tốc là :
221
2
121
2
21
2
2
2
1
2
1
2
2
2
2
2
2cos)(2)(
aaaayxv
(2.13)
Do vậy động năng của khâu 2 là:
221
2
1212
2
21
2
22
2
1
2
1
2
12
2
1
2
22
2
1
2cos)()(
aamamamvmK
(2.14)
Thế năng cho khâu 2 là:
)]sin(sin[ 212112222
aagmgymP
(2.15)
y (x2,y2)
m2
a2 2
g
a1 1 m1
x
0
Chương 5: Động lực học robot và ứng dụng trong điều khiển
67
Phương trình Lagrange
Hàm Lagrange cho Tay máy này là:
)sin(sin)(cos)(
)()(
21221121221
2
1212
2
21
2
22
2
1
2
1
2
121
2
1
2121
gamgammaam
amammPPKKPKL
(2.16
)
Ta cần xác định các biểu thức :
)cos(sin)(
sincos)(
cos)(
)cos(cos)(
cos)2(cos)2()()(
cos)2()()(
2122221
2
1212
2
2212122121221
2
22
2
2121221
2
22
2
21221121
1
2
2
22121222121221
2
221
2
121
1
22121221
2
221
2
121
1
gamaam
L
aamaamam
L
dt
d
aamam
L
gamgamm
L
aamaamamamm
L
dt
d
aamamamm
L
Cuối cùng, phương trình chuyển động của cơ hệ tay máy được cho bởi hệ
hai phương trình vi phân:
)θθ(θ)(
θ)θθθ2(θ]θ[
θ]θ2)[(τ
21221121
2
2
22121222212
2
22
1221
2
22
2
1211
cosgamcosgamm
sinaamcosaamam
cosmmamamm
)θθ(
θθθθ]θ[τ
2122
2
2
12122
2
2212212
2
222
cosgam
sinaamamcosaamam
Biểu diễn phương trình chuyển động của cơ hệ Tay máy dưới dạng ma trận
Dưới dạng ma trận, phương trình chuyển động hay phương trình động lực
học Tay máy dưới dạng ma trận có thể viết như sau:
(2.18)
Chương 5: Động lực học robot và ứng dụng trong điều khiển
68
2
1
2122
21221121
2
2
1212
2
2
221212
2
1
2
222212
2
22
2212
2
22221
2
22
2
121
τ
τ
)θθ(
)θθ(θ)(
θθ
θ)θθθ2(
θ
θ
θ
θθ2)(
cosgam
cosgamcosgamm
sinaam
sinaam
amcosaamam
cosaamamcosmmamamm
Ta tìm được biểu thức động lực học tay máy dưới dạng chuẩn, được biểu
diễn chung dưới dạng sau :
τ)q()q,q(q)q( GVM
(2.20)
M(q) là ma trận quán tính,
)q,q(
V
là vectơ lực Coriolis hoặc/và lực hướng
tâm và G(q) là vectơ trọng lực.
Với biểu thức trên M(q) là ma trận đối xứng.
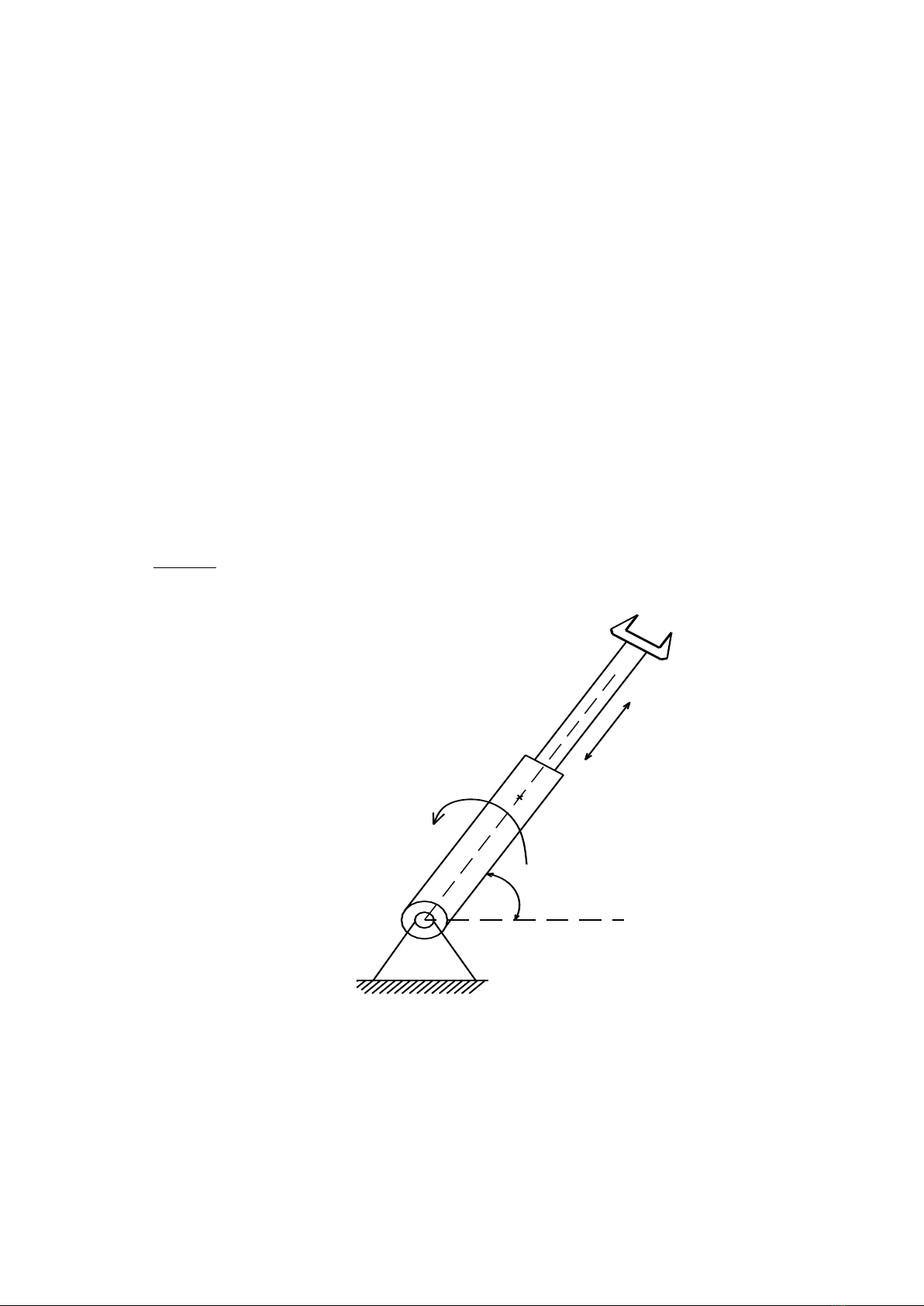
b. Ví dụ 2.
Xây dựng Phương trình động lực học của robot hai bậc tự do cấu hình RT.
d2
Hình 5.3. Cấu hình của Robot 2 bậc tự do RP
Xuất phát từ phương pháp động lực học cho hệ cơ học tổng quát
Phương trình chuyển động Lagrange thiết lập cho một cơ hệ được cho bởi:
2
0
O
(2.19)