Chương 2: Phân tích hệ cơ cân bằng tĩnh và chuyển động tay máy
18
18
Chương 2
PHÂN TÍCH HỆ CƠ CÂN BẰNG TĨNH VÀ
CHUYỂN ĐỘNG CỦA TAY MÁY
2.1. Các khái niệm cơ bản và tiền đề tĩnh học
2.1.1. Trạng thái cân bằng
Hệ vật được xem như ở trạng thái cân bằng khi tổng các ngoại lực tác động
lên nó bằng không. Lúc ấy hệ vật hoặc đừng yên hoặc chuyển động thẳng đều
đối với hệ qui chiếu đó.
Trong thực tế luôn tồn tại lực ma sát nên khi hệ vật đạt trạng thái cân bằng
thì nó đứng yên.
2.1.2. Lực
Lực đặc trưng cho tác dụng cơ học của vật thể này lên vật thể khác
Lực được biểu diễn bằng một vector {phương, chiều, độ lớn, điểm đặt}
Trong hệ trục {x,y,z} thì lực
),,( zyx FFFF
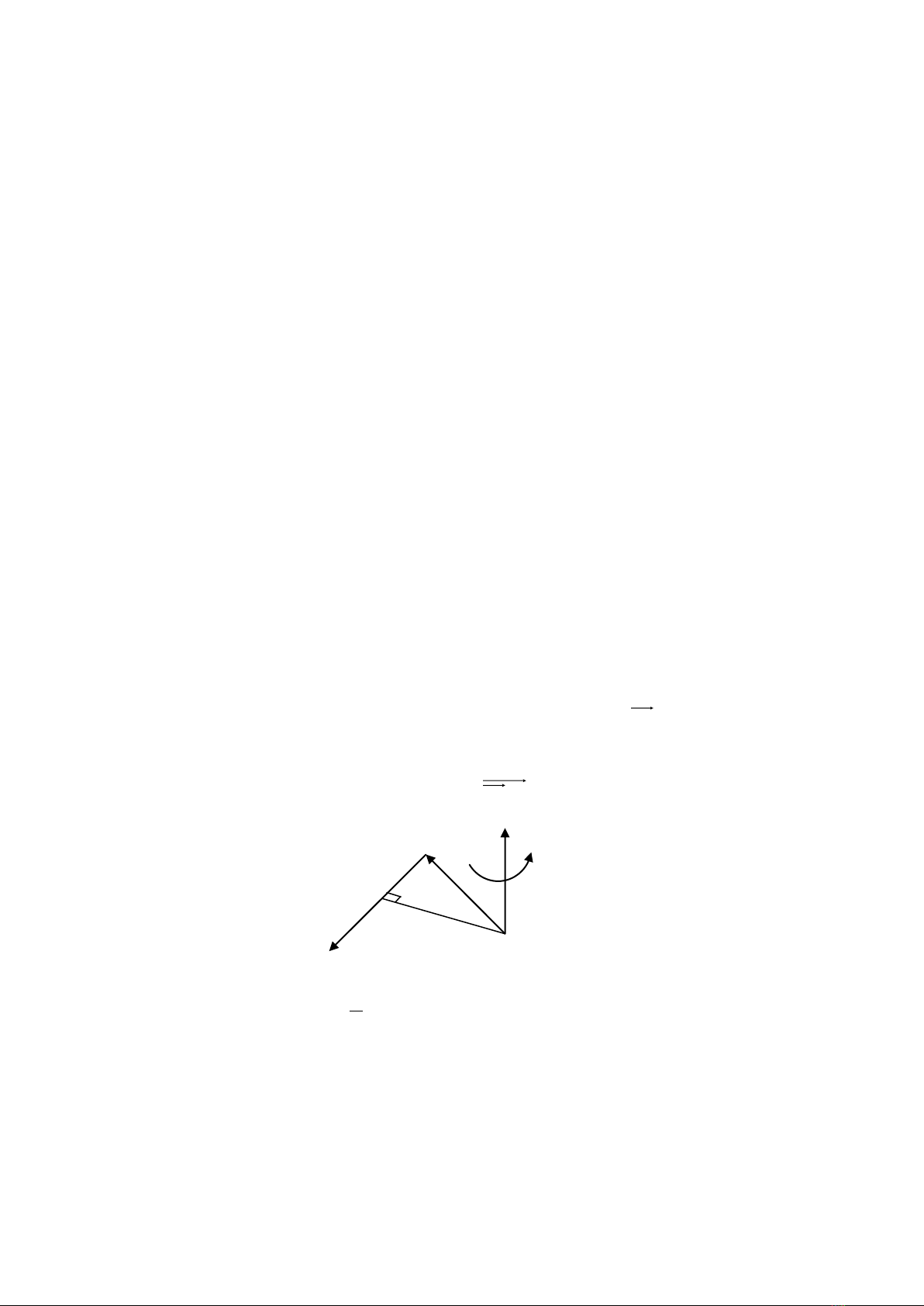
2.1.3. Mômen của lực đối với tâm
Mômen của lực
F
đặt tại A đối với tâm O là
FdFOAFm
)(
0
)(
0Fm
có độ lớn bằng d.F, điểm đặt tại O, phương vuông góc với mặt phẳng
),( OF
, chiều thuận theo chiều xoay của
FOA
,
2.1.4. Momen của lực đối với trục (∆)
Tách
FFF
//
=>
Vậy momen cua lực đối với trục bằng tích của thành phần hình chiếu vuông
góc của lực (lên mặt phẳng vuông góc với trục) với khoãng cách từ lực hình
chiếu đến trục.
Chiều của momen hường theo chiều xoay của lực quanh trục.
)(
0Fm
O
A
F
d
Chương 2: Phân tích hệ cơ cân bằng tĩnh và chuyển động tay máy
19
19
2.1.5. Hệ lực
Hệ lực tác dụng vào một vật đang khảo sát
),...,,()( 21 nk FFFF
Hai hệ lực
khi chúng có cùng tác dụng cơ học
Hợp lực của hệ lực:
R
được gọi là hợp lực của hệ lực
)( k
F
khi
k
FR
Hệ lực cân bằng khi
0R
2.1.6. Các tiên đề tĩnh học
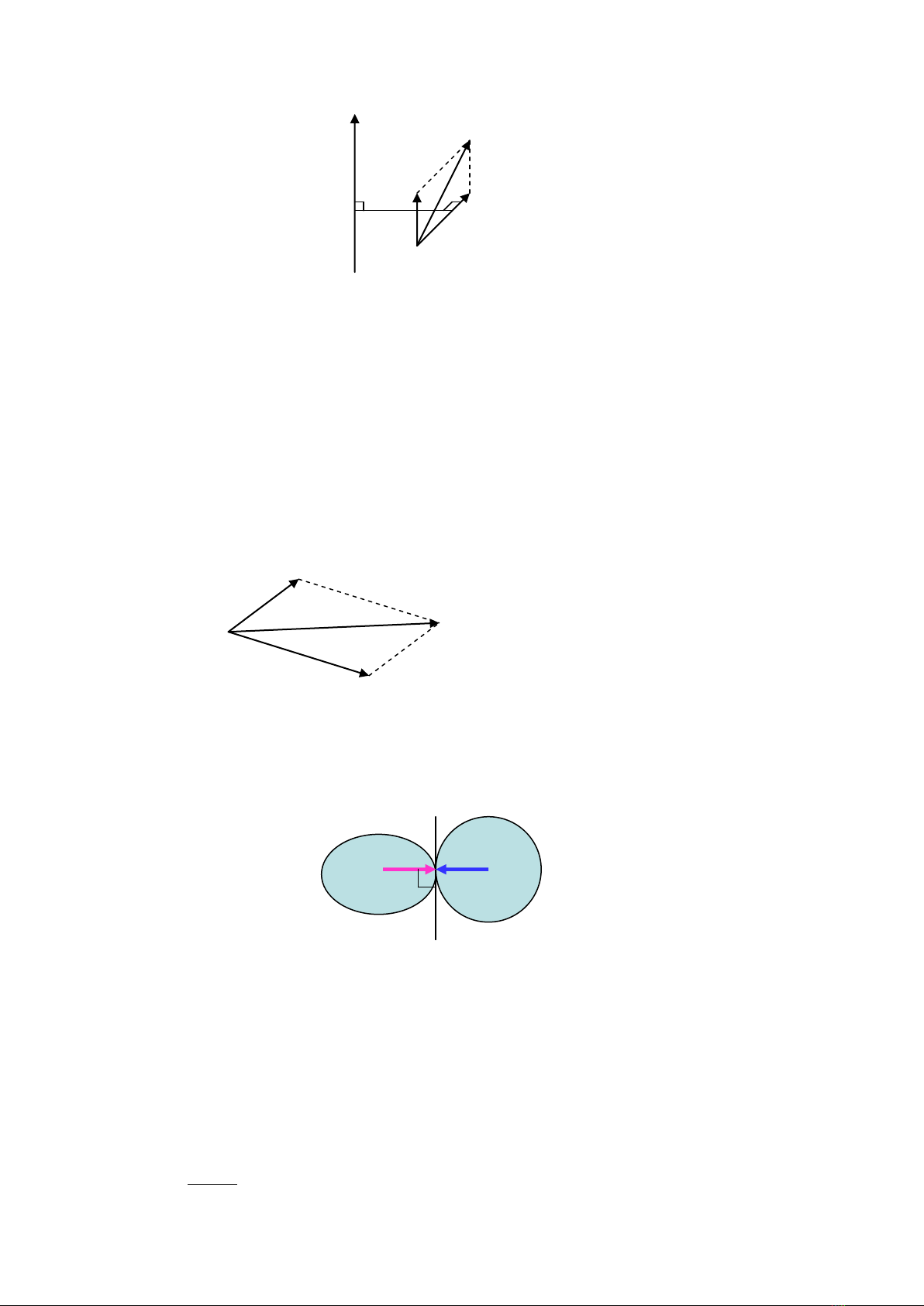
Hai lực cân bằng khi chúng cùng phương, ngược hướng, cùng độ lớn.
Hợp lực của hai lực là vector lực đường chéo của hình bình hành.
21 FFR
Khi hai vật tương tác với nhau, chúng tác lên nhau một lực:
Hai lực tương tác cùng phương, cùng độ lớn, nhưng ngược hướng.
Điểm đặt của 2 lực nằm ngay tại vị trí tiếp xúc của 2 vật và hướng vuông
góc với tiếp tuyến tại điểm tiếp xúc.
Vật tự do là vật có thể dịch chuyển tùy ý trong lân cận bé từ vị trí đang xét.
Ngược lại gọi là vật không tự do
Vật khảo sát (S) được qui ước gọi là vật chịu liên kết. Các vật khác tương
tác cơ học với S được gọi là vật gây liên kết.
Vật không tự do có thể xem là tự do nếu ta thay thế các vật gây liên kết
bằng các phản lực liên kết.
Ví dụ :
Tiếp tuyến
F
N
O
)(
F
F
//
F
d
1
F
2
F
R
Chương 2: Phân tích hệ cơ cân bằng tĩnh và chuyển động tay máy
20
20
Điều kiện cân bằng của hệ tĩnh
0
0
0)(
0
M
R
Fk
, trong đó
R
là vector hợp lực và
0
M
là mô men
chính với tâm O của hệ
)( k
F
.
Ta có
k
kzz
k
kyy
k
kxx
zyx
FR
FR
FR
RRRR ),,(
, và
k
kzoz
k
kyoy
k
kxox
ozoyox
FmM
FmM
FmM
MMMM
)(
)(
)(
),,(
0
Vậy điều kiện để hệ cân bằng tĩnh là
k
kz
k
ky
k
kx
k
kz
k
ky
k
kx
Fm
Fm
Fm
F
F
F
F
0)(
0)(
0)(
0
0
0
0)(
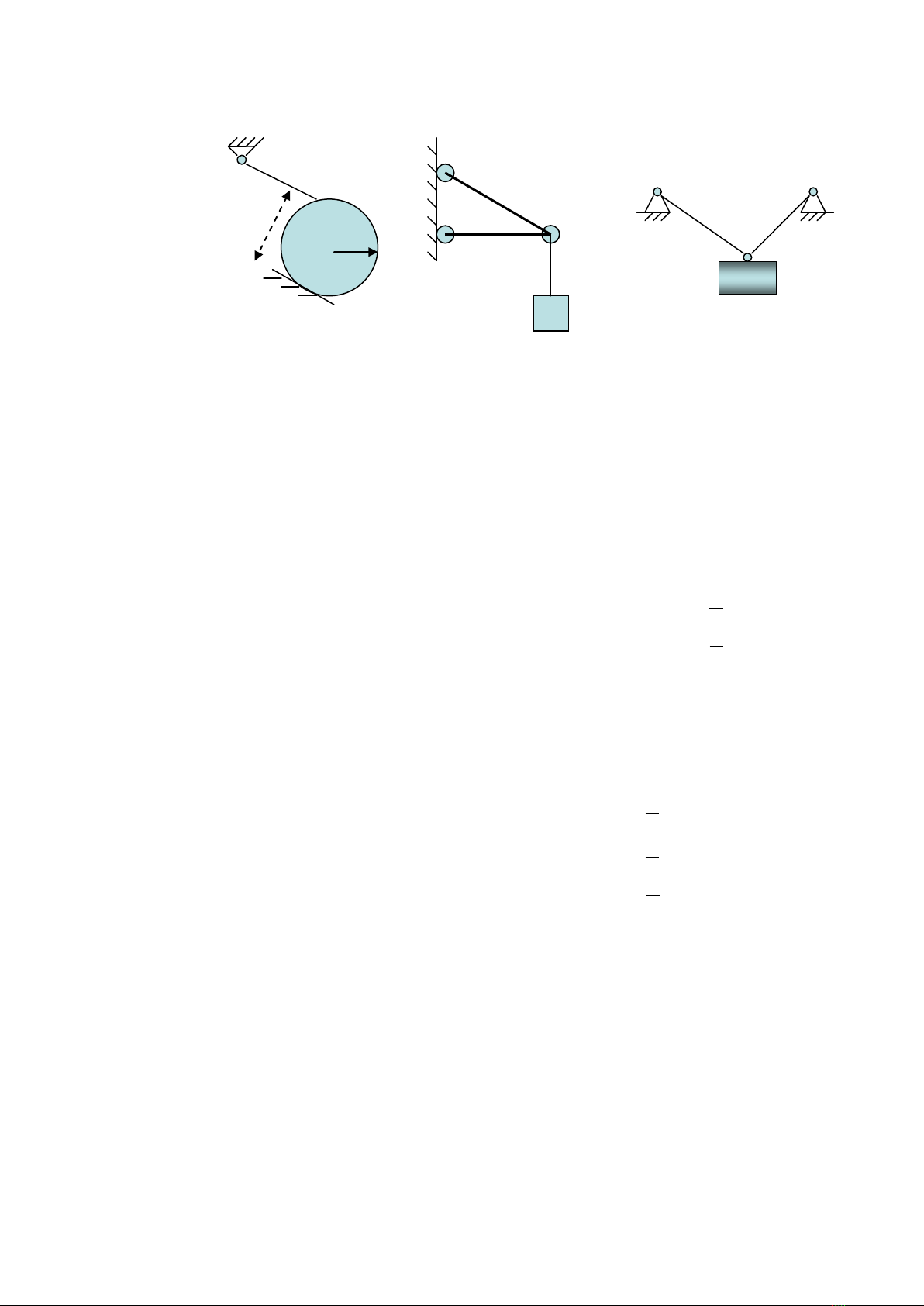
2.1.7. Một số mô hình phản lực liên kết
a. Phản lực liên kết một chiều
●
r
h
M
m
m
Chương 2: Phân tích hệ cơ cân bằng tĩnh và chuyển động tay máy
21
21
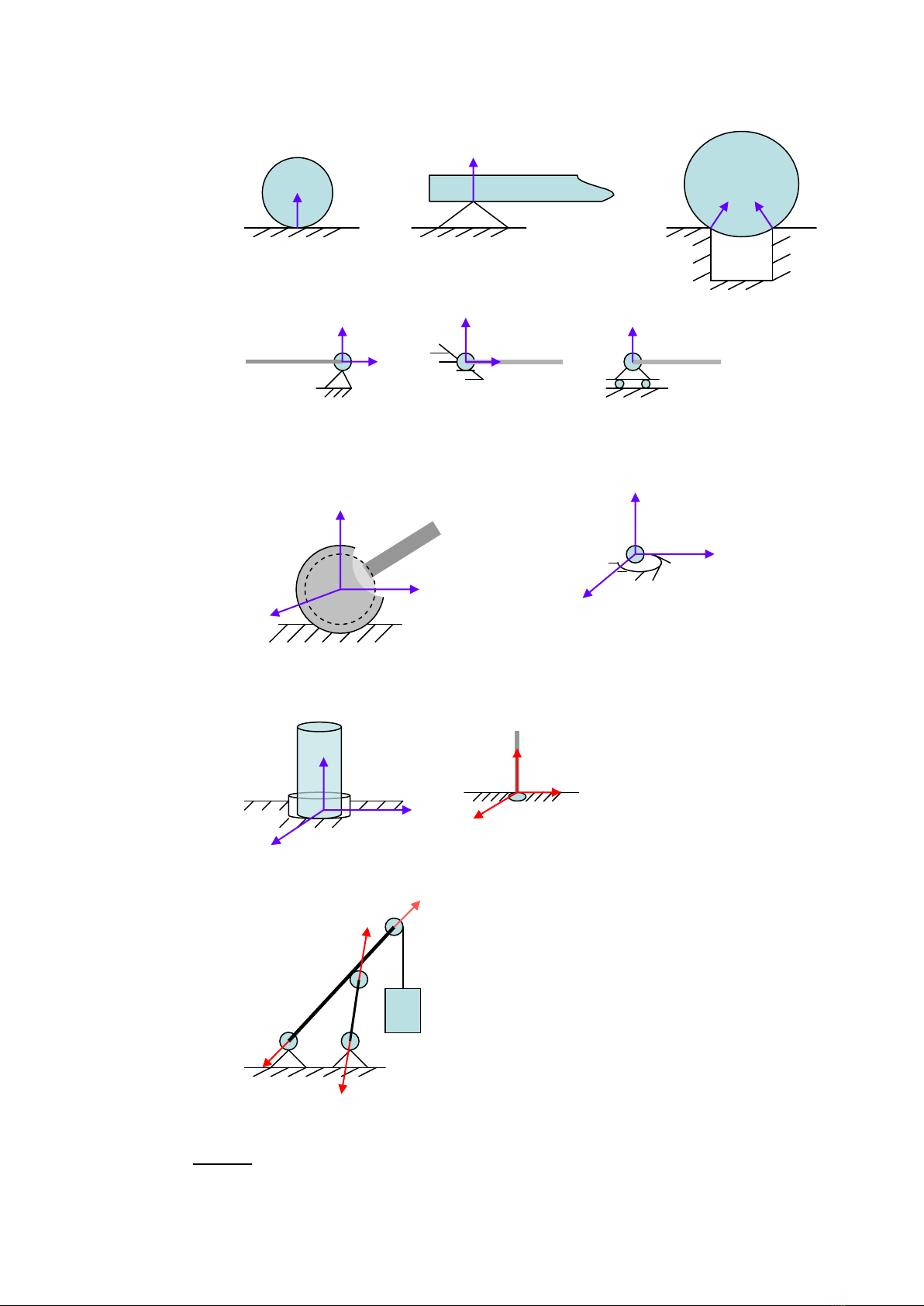
b. Liên kết bản lề trụ
c. Liên kết bản lề cầu
d. Liên kết gối đỡ
e. Liên kết thanh
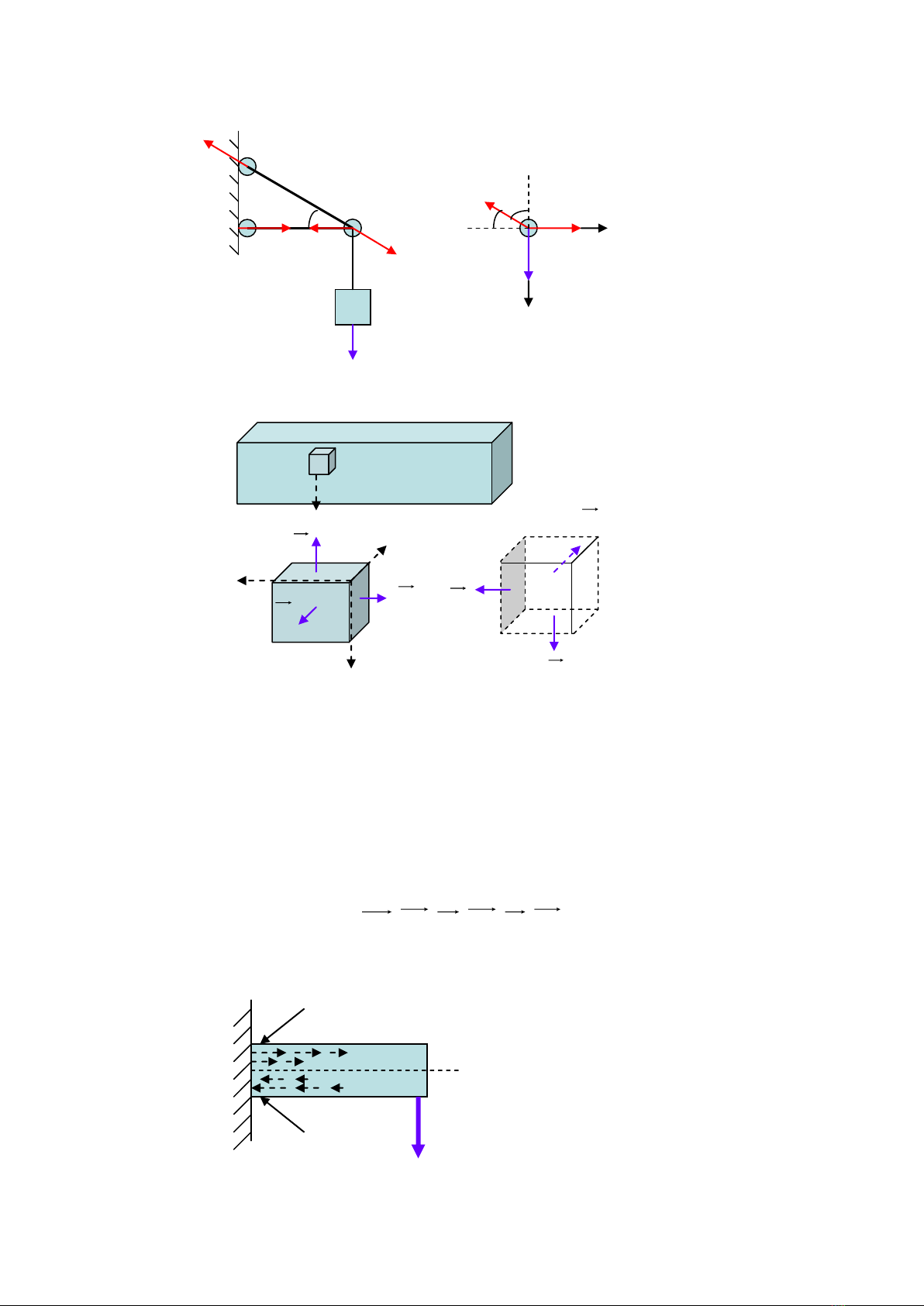
Vi dụ: Xác định các phản lực liên kết của thanh trong hệ sau
N
N
s
s
1
N
2
N
s
s
s
x
R
y
R
z
R
Ký hiệu qui ýớc
Ký hiệu qui ước
ước
Chương 2: Phân tích hệ cơ cân bằng tĩnh và chuyển động tay máy
22
22
2.1.8. Sức bền của vật liệu
a. Các tác động lực lên thanh bao gồm:
Lực kéo: làm cho thanh dãn ra theo hai chiều của lực
Lực nén: làm cho thanh nén lại theo hai chiều của lực
Lực xoắn: làm cho thanh vặn cong
Dưới tác động của các ngoại lực mỗi phần tử dv(dx,dy,dz) đều chịu tác
động của các vector lực, được gọi là các tensor ứng suất. Các vector ứng suất
này có được thể hiện như hình vẽ, theo từng cặp vector bằng nhau về độ lớn
nhưng ngược chiều nhau,
),,,,,( ,,, dzdzdydydxdx
.
b. Trạng thái vật lý của thanh khi bị xoắn
Nửa trên của thanh có xu
hướng bị kéo giãn ra
Nửa dưới của thanh có xu
hướng bị nén lại
F
bị kéo giãn
bị nén lại
Thanh liên kết
dx
dy
dz
x
y
z
,
y
,
x
,
z
m(5kg)
450
P
A
1
A
2
A
P
y