1
Kỹ Thuật Số
Kỹ Thuật Số
2
Ch ng 4ươ
M ch t h pạ ổ ợ
(Combinational Circuits)
3
Khái ni m v m ch t h p.ệ ề ạ ổ ợ
Ph ng pháp phân tích m t m ch t h p có s n.ươ ộ ạ ổ ợ ẵ
Ph ng pháp thi t k m ch t h p dùng các c ng logic ươ ế ế ạ ổ ợ ổ
c b n.ơ ả
Tìm hi u m t s m ch t h p thông d ng.ể ộ ố ạ ổ ợ ụ
Ph ng pháp thi t k m ch t h p s d ng các m ch t ươ ế ế ạ ổ ợ ử ụ ạ ổ
h p có s nợ ẵ
4
4.1
4.1 Gi i thi uớ ệ
Gi i thi uớ ệ
M ch s th ng đ c chia làm hai lo i: m ch t h p ạ ố ườ ượ ạ ạ ổ ợ
(combinational circuit) và m ch tu n t (sequential circuit).ạ ầ ự
M ch t h p là m ch mà các ngõ ra ch ph thu c vào các m c ạ ổ ợ ạ ỉ ụ ộ ứ
logic c a các ngõ vào t i th i đi m đó. M ch t h p không có ủ ạ ờ ể ạ ổ ợ
thu c tính nh . Trong m ch t h p không có b t kỳ vòng h i ti p ộ ớ ạ ổ ợ ấ ồ ế
nào.
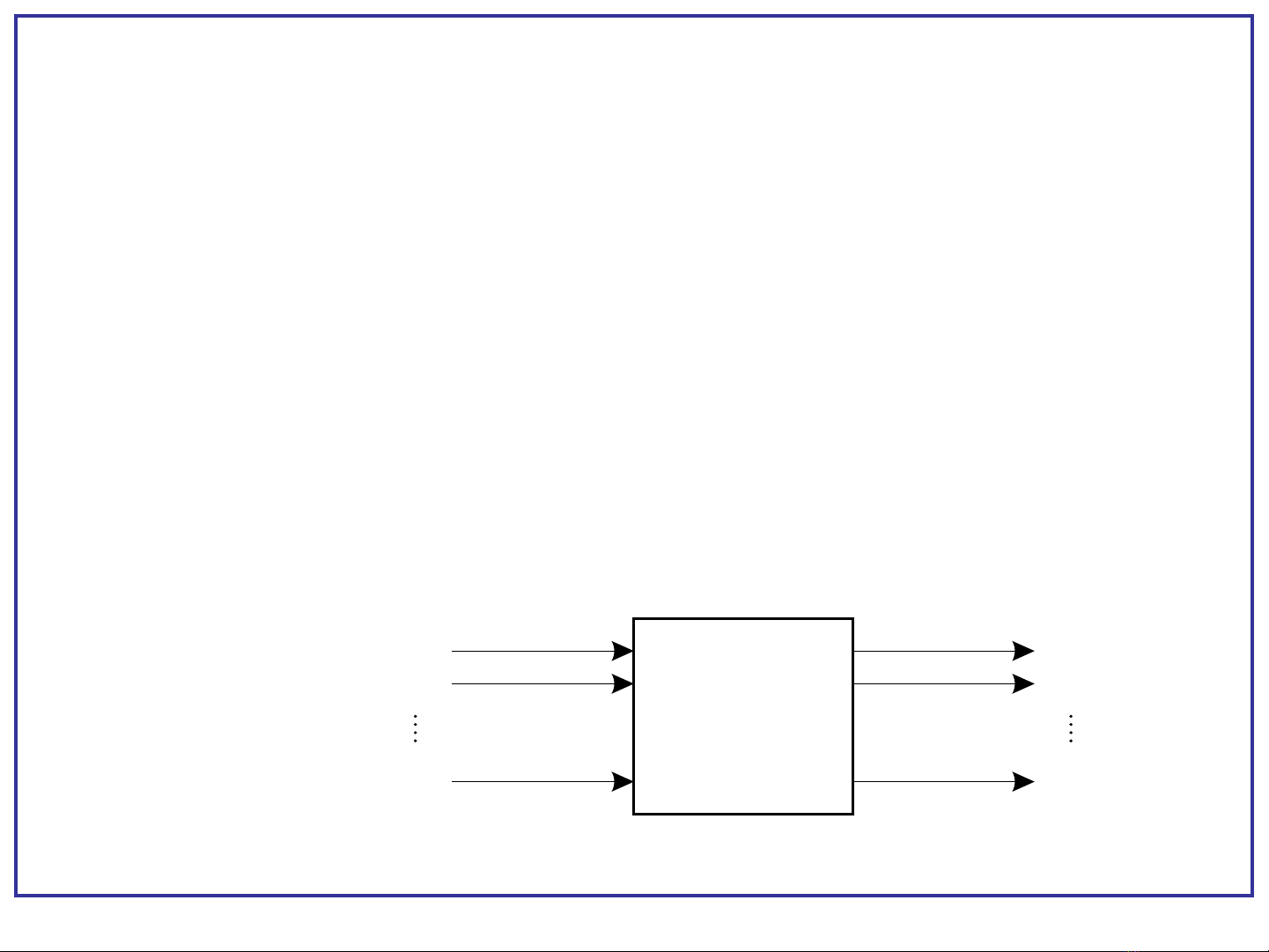
S đ t ng quát:ơ ồ ổ
Maïch toå
hôïp
X1
X2
Xn
Y1
Y2
Ym
5
4.2
4.2 Phân tích m ch t h pạ ổ ợ
Phân tích m ch t h pạ ổ ợ
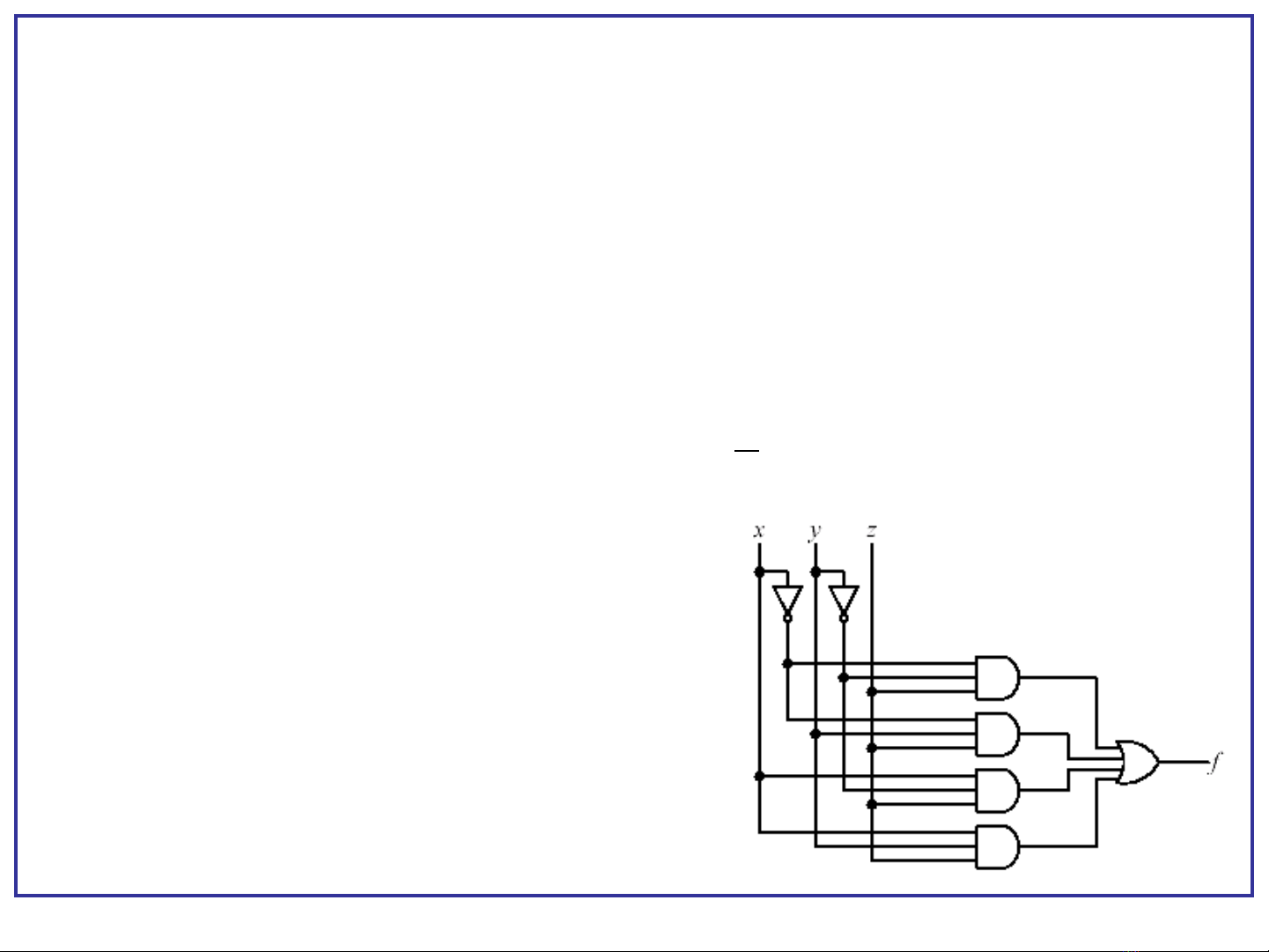
Phân tích m ch logic cho hình sau:ạ ở
Ví dụ minh họa:
Ví dụ minh họa:
Cho tr c m t m ch logic và các tín hi u vào, hãy xác đ nh ướ ộ ạ ệ ị
hàm logic ngõ ra theo các tín hi u vào đó. Hàm logic ngõ ra có th ệ ể
đ c bi u di n b i b ng s th t ho c các bi u th c logic.ượ ể ễ ở ả ự ậ ặ ể ứ
Đặt vấn đề:
Đặt vấn đề: