Khóa học LTĐH môn Toán – Thầy Đặng Việt Hùng Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH và Luyện giải đề tại Moon.vn để đạt được kết quả cao nhất trong kỳ TSĐH 2014!
I. BÀI TOÁN TÌM ĐIỂM THUỘC MẶT PHẲNG CÓ YẾU TỐ CỰC TRỊ
Dạng 1: Tìm điểm M thuộc (P) sao cho
= + +

u aMA bMB cMC
có
u
đạt min.
Phương pháp giải:
+ Tìm điểm I thỏa mãn hệ thức
0
aIA bIB cIC
+ + =
+ Phân tích
(
( ) ( )
u aMA bMB cMC a b c MI aIA bIB cIC a b c MI
= + + = + + + + + = + +
Khi đó
min
u a b c MI u
= + + ⇒⇔
M là hình chiếu vuống góc của I lên (P).
Tọa độ điểm
( ; ; )
M x y z
thỏa mãn hệ phương trình
( )
∈
=
P
M P
IM kn
Ví dụ 1.
Cho các
đ
i
ể
m A(2; 1; −1), B(0; 3; 1) và
( ) : 3 0.
P x y z
+ − + =
Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho
a)
min
+
MA MB
b)
min
2
MA MB
−
Đ/s: a)
(1;2;0), ( 1;0;2).
I M
−
b)
(4; 1; 3), (1; 4;0).
I M
− − −
Ví dụ 2. Cho các điểm
A
(1; 0; −1),
B
(2; −2; 1),
C
(0; −1; 0) và
( ) : 2 2 6 0.
− + + =
P x y z
Tìm điểm
M
thuộc
(
P
) sao cho
a)
min
+ +
MA MB MC
b)
min
2 4 3− +
MA MB MC
Đ/s: a)
(0;1; 2).
≡ −
M G
b)
32 89 10
( 6;5; 6), ; .
9 9 9
− − − −
I M
Ví dụ 3.
Cho các
đ
i
ể
m A(1; 1; 2), B(−2; 1; −7) và
( ) : 1 0.
+ − + =
P x y z
Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho
a)
min
+
MA MB
b)
min
2+

MA MB
Đ/s:
b)
(0;1; 1)
−
I
Ví dụ 4.
Cho các
đ
i
ể
m A(0; 1; −1), B(2; 3; −2), C(6; 1; 14) và
( ) : 2 1 0.
+ − + =
P x y z
Tìm
đ
i
ể
m M thu
ộ
c (P)
sao cho
min
2 3+ −
MA MB MC
Đ/s:
(
)
(2;2;1), 1;0;2 .
I M
Dạng 2: Tìm điểm M thuộc (P) sao cho
=++
2 2 2
T aMA bMB cMC
đạt max hoặc min.
Ph
ươ
ng pháp gi
ả
i:
+) Tìm
đ
i
ể
m I th
ỏ
a mãn h
ệ
th
ứ
c
0
aIA bIB cIC
+ + =
+) Phân tích
2 2 2 2
( )= + + + + +
T a b c MI aIA bIB cIC
+) N
ế
u a + b + c > 0 thì T
đặ
t min; a + b + c < 0 thì T
đặ
t max
14. CỰC TRỊ TRONG TỌA ĐỘ KHÔNG GIAN – P1
Thầy Đặng Việt Hùng
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH môn Toán – Thầy Đặng Việt Hùng Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH và Luyện giải đề tại Moon.vn để đạt được kết quả cao nhất trong kỳ TSĐH 2014!
Khi đó
ax min min
;
⇔ →
m
T T MI M là hình chiếu vuống góc của I lên (P).
Tọa độ điểm
( ; ; )
M x y z
thỏa mãn hệ phương trình
( )
∈
=
P
M P
IM kn
Ví dụ 1.
Cho các
đ
i
ể
m A(
−
3; 5;
−
5), B(5;
−
3; 7) và
( ) : 0.
+ + =
P x y z
Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho
a)
2 2
= +
T MA MB
đạ
t giá tr
ị
nh
ỏ
nh
ấ
t.
b)
2 2
2
= −
T MA MB
đạ
t giá tr
ị
l
ớ
n nh
ấ
t.
Đ/s:
a)
(1;1;1); (0;0;0)
I M
b)
(13; 11;9), (6; 18;12).
− −
I M
Ví dụ 2.
Cho các
đ
i
ể
m A(1; 4; 5), B(0; 3; 1), C(2;
−
1; 0) và
( ) : 3 3 2 15 0.
− − − =
P x y z
Tìm
đ
i
ể
m M thu
ộ
c
(P) sao cho
a)
2 2 2
=++
T MA MB MC
đạ
t giá tr
ị
nh
ỏ
nh
ấ
t.
b)
2 2 2
2 4
= + −
T MA MB MC
đạ
t giá tr
ị
l
ớ
n nh
ấ
t.
Đ/s:
a)
(4; 1;0)
≡ −
M G là tr
ọ
ng tâm tam giác
b)
25 74 9
(7; 16; 7), ; .
11 11 11
− − − −
I M
Ví dụ 3.
Cho các
đ
i
ể
m A(1; 1; -1), B(2; 0; 1), C(1; −1; -1) và
( ) : 2 0.
+ + + =
P x y z
Tìm
đ
i
ể
m M thu
ộ
c (P)
sao cho
a)
2 2
2
= +
T MA MB
đạ
t giá tr
ị
nh
ỏ
nh
ấ
t.
b)
2 2 2
2= + −
T MA MB MC
đạ
t giá tr
ị
l
ớ
n nh
ấ
t.
Đ/s:
b)
(
)
(2;1;1), 0; 1; 1 .
− −
I M
Ví dụ 4.
Cho các
đ
i
ể
m A(0; 4; -2), B(1; 2; -1) và
( ) : 1 0.
− + + =
P x y z
Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho bi
ể
u
th
ứ
c
2 2
2
−
MA MB
đạ
t giá tr
ị
l
ớ
n nh
ấ
t?
Đ/s:
(
)
(2;0;0), 1;1; 1 .
−
I M
Ví dụ 5.
Cho các
đ
i
ể
m A(1; 1; 0), 5
; 1;0 ,( ) : 2 0
3
− − + =
B P x y z . Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho bi
ể
u th
ứ
c
2 2
3−
MA MB
đạ
t giá tr
ị
l
ớ
n nh
ấ
t?
Đ/s:
(
)
(2; 2;0), 1;0; 1 .
− −
I M
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH môn Toán – Thầy Đặng Việt Hùng Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH và Luyện giải đề tại Moon.vn để đạt được kết quả cao nhất trong kỳ TSĐH 2014!
I. BÀI TOÁN TÌM ĐIỂM THUỘC MẶT PHẲNG CÓ YẾU TỐ CỰC TRỊ
Dạng 3: Tìm điểm M thuộc (P) sao cho
(
+
min
MA MB
hoặc
−
max
MA MB
Phương pháp giải:
+) Kiểm tra vị trí tương đối của các điểm A và B so với mặt phẳng (P).
+) Nếu A và B cùng phía (P) thì bài toán min phải lấy đối xứng A qua (P), bài toán tìm max là giao điểm
trực tiếp của đường thẳng AB và (P).
+) Nếu A và B khác phía (P) thì bài toán max phải lấy đối xứng A qua (P), bài toán tìm min là giao điểm trực
tiếp của đường thẳng AB và (P).
Ví dụ 1. Cho hai điểm A(3; 1; 1), B(7; 3; 9) và (P): x + y + z + 3 = 0.
a) Tìm điểm M∈(P) sao cho +
MA MB
đạt giá trị nhỏ nhất.
b) Tìm điểm N∈(P) sao cho NA
2
+ NB
2
đạt giá trị nhỏ nhất.
Đ/s: M(0; –3; 0)
Ví dụ 2. Cho ba điểm A(4; –1; 2), B(3; 5; –1),vC(2; 5; –1) và (P): x + 2y – z – 3 = 0
a) Tìm điểm M∈(P) sao cho + +
MA MB MC
đạt giá trị nhỏ nhất.
b) Tìm điểm N∈(P) sao cho NA
2
+ NB
2
+ NC
2
đạt giá trị nhỏ nhất.
Đ/s: M(2; 1; 1).
Ví dụ 3. Cho hai điểm A(–1; 3; –2), B(–9; 4; 9) và (P): 2x – y + z + 1 = 0.
a) Chứng tỏ rằng đường thẳng đi qua A, B cắt mặt phẳng (P) tại một điểm I, tìm toạ độ điểm đó.
b) Tìm điểm M thuộc (P) sao cho AM + BM nhỏ nhất.
Đ/s: a) I(7; 2; –13) b) M(–1; 2; 3)
Ví dụ 4. Cho hai điểm A(1; 2; 3), B(4; 4; 5) và mặt phẳng (P): x – y + z – 1 = 0.
a) Chứng tỏ rằng đường thẳng đi qua A, B cắt mặt phẳng (P) tại một điểm I, tìm toạ độ điểm đó .
b) Tìm điểm M thuộc (P) sao cho |MA – MB| lớn nhất.
Đ/s:
4 7
0; ;
3 3
I , M trùng I.
Ví dụ 5.
Cho hai
đ
i
ể
m A(1; 0; 2), B(2; 1; 3) và (P): x – 2y + z – 4 = 0.
Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho AM + BM nh
ỏ
nh
ấ
t.
Ví dụ 6.
Cho hai
đ
i
ể
m A(–4; 1; 2), B(–3; 1; 3) và (P): x – y + z + 2 = 0.
Tìm
đ
i
ể
m M thu
ộ
c (P) sao cho AM + BM nh
ỏ
nh
ấ
t.
Ví dụ 7.
Cho m
ặ
t ph
ẳ
ng (P): x + y + z – 1 = 0 và hai
đ
i
ể
m A(1, –3, 0), B(5, –1, –2).
a)
Ch
ứ
ng t
ỏ
r
ằ
ng
đườ
ng th
ẳ
ng
đ
i qua A, B c
ắ
t m
ặ
t ph
ẳ
ng (P) t
ạ
i m
ộ
t
đ
i
ể
m I, tìm to
ạ
độ
đ
i
ể
m
đ
ó .
14. CỰC TRỊ TRONG TỌA ĐỘ KHÔNG GIAN – P2
Thầy Đặng Việt Hùng
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH môn Toán – Thầy Đặng Việt Hùng Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH và Luyện giải đề tại Moon.vn để đạt được kết quả cao nhất trong kỳ TSĐH 2014!
b) Tìm toạ độ điểm M trên mặt phẳng (P) sao cho |MA – MB| đạt giá trị lớn nhất.
II. BÀI TOÁN TÌM ĐIỂM THUỘC ĐƯỜNG THẲNG CÓ YẾU TỐ CỰC TRỊ
Ví dụ 1. Cho hai điểm A(1; 1; 2), B(-1; 0; 1) và
1 1
:
2 1 1
− +
= =
x y z
d. Tim
đ
i
ể
m M trên d sao cho
a)
di
ệ
n tích tam giác MAB nh
ỏ
nh
ấ
t.
b)
MA + MB
đạ
t giá tr
ị
nh
ỏ
nh
ấ
t.
Đ
/s: b)
1
.
6
=
t
Ví dụ 2.
Cho hai
đ
i
ể
m A(0; 1; -1), B(3; 0; 1) và
1 2
:
1 1 1
− +
= =
−
x y z
d. Tim
đ
i
ể
m M trên d sao cho MA + MB
đạ
t giá tr
ị
nh
ỏ
nh
ấ
t.
Đ
/s:
1
.
3
= −
t
Ví dụ 3.
Cho hai
đ
i
ể
m A(0; 1; -1), B(2; 0; 1) và 1
:
1 1 2
+
= =
−
x y z
d. Tim
đ
i
ể
m M trên d sao cho
a)
MA + MB
đạ
t giá tr
ị
nh
ỏ
nh
ấ
t.
b)
Di
ệ
n tích tam giác MAB nh
ỏ
nh
ấ
t.
c)
Kho
ả
ng cách t
ừ
M t
ớ
i (P) b
ằ
ng hai l
ầ
n kho
ả
ng cách t
ừ
M t
ớ
i (Q) bi
ế
t
( ) : 2 2 1 0
( ) : 2 2 3 0
+ + − =
− − + =
P x y z
Q x y z
Đ
/s: a)
7 42 50
26
−
=t b)
8
5
= −
t c) 11
; 5
5
= = −
t t
Ví dụ 4.
Cho ba
đ
i
ể
m A(1; 0; –1), B(0; 2; 3), C(-1; 1; 1) và
đườ
ng th
ẳ
ng 1 1
: .
1 2 2
+ −
= =
−
x y z
d Tìm
đ
i
ể
m M
trên d sao cho
a)
2 2 2
2 4+ −
MA MB MC
đạt giá trị lớn nhất?
b)
min
+
AM BC
Đ/s: a)
4
9
= −
t b)
5
9
=
t
Ví dụ 5. Cho các điểm A(2; 1; –1), B(1; 2; 1), C(0; 0; 3) và
1 5
:
3 1 1
− −
= =
x y z
d. Tìm điểm M thuộc d sao
cho MA
2
+ MB
2
+ MC
2
đạt giá trị nhỏ nhất.
Đ/s:
3 12 54
; ; .
11 11 11
−
M
Ví dụ 6. Cho ba điểm A(1; –2; 1), B(2; –1; –4), C(3; 0; –2) và đường thẳng
1 3 1
: .
2 1 2
− − −
= =
−
x y z
d
a) Tìm trên d một điểm M sao cho 2+ −
MA MB MC
nhỏ nhất.
b) Tìm điểm M thuộc d sao cho –MA
2
+ MB
2
–MC
2
đạt giá trị lớn nhất.
Ví dụ 7. Cho A(1; 1; 0), B(3; –1; 4) và
1 1 2
: .
1 1 2
+ − +
= =
−
x y z
d
Tìm điểm M thuộc d sao cho MA + MB đạt giá trị nhỏ nhất.
Đ/s: M(1; –1; 2)
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
Khóa học LTĐH môn Toán – Thầy Đặng Việt Hùng Facebook: LyHung95
Tham gia trọn vẹn khóa LTĐH và Luyện giải đề tại Moon.vn để đạt được kết quả cao nhất trong kỳ TSĐH 2014!
III. BÀI TOÁN KHOẢNG CÁCH CÓ YẾU TỐ CỰC TRỊ
Phương pháp đại số:
+) Gọi véc tơ pháp tuyến hoặc véc tơ chỉ phương của mặt phẳng (hoặc đường thẳng) cần lập là (a; b; c)
+) Thiết lập một phương trình quy ẩn (a theo b, c hoặc ngược lại) từ một dữ kiện về mặt phẳng chứa đường,
song song hoặc vuông góc. Giả sử phương trình thu gọn ẩn là a = f(b; c)
+) Thiết lập phương trình khoảng cách mà đề bài yêu cầu, thay a = f(b; c) vào ta được một phương trình hai
ẩn b; c.
Xét hàm khoảng cách
( ; )
=
d g b c
+) Nếu c = 0 thì
1
0
≠ → =
b d d
, lưu lại giá trị khoảng cách d
1
này.
+) Nếu
0 ( );
≠⇒= = =
b b
c d g g t t
c c
Kh
ả
o sát hàm g(t) ta thu
đượ
c k
ế
t qu
ả
.
Chú ý:
+) Công th
ứ
c kho
ả
ng cách t
ừ
m
ộ
t
đ
i
ể
m
đế
n m
ộ
t m
ặ
t ph
ẳ
ng
( )
0 0 0
2 2 2
;( )
+ + +
=+ +
Ax By Cz D
d A P
A B C
+) Công th
ứ
c kho
ả
ng cách t
ừ
m
ộ
t
đ
i
ể
m
đế
n m
ộ
t
đườ
ng th
ẳ
ng
( )
;
;∆
∆
∆ =
u AM
d A
u; v
ớ
i M thu
ộ
c
∆
.
+) Công th
ứ
c kho
ả
ng cách gi
ữ
a hai
đườ
ng th
ẳ
ng
( )
1 2 1 2
1 2
1 2
; .
;
;
∆ ∆
∆ ∆
∆ ∆ =
u u M M
d
u u
Bây giờ chúng ta xét bản chất hình học của các bài toán về khoảng cách thường gặp
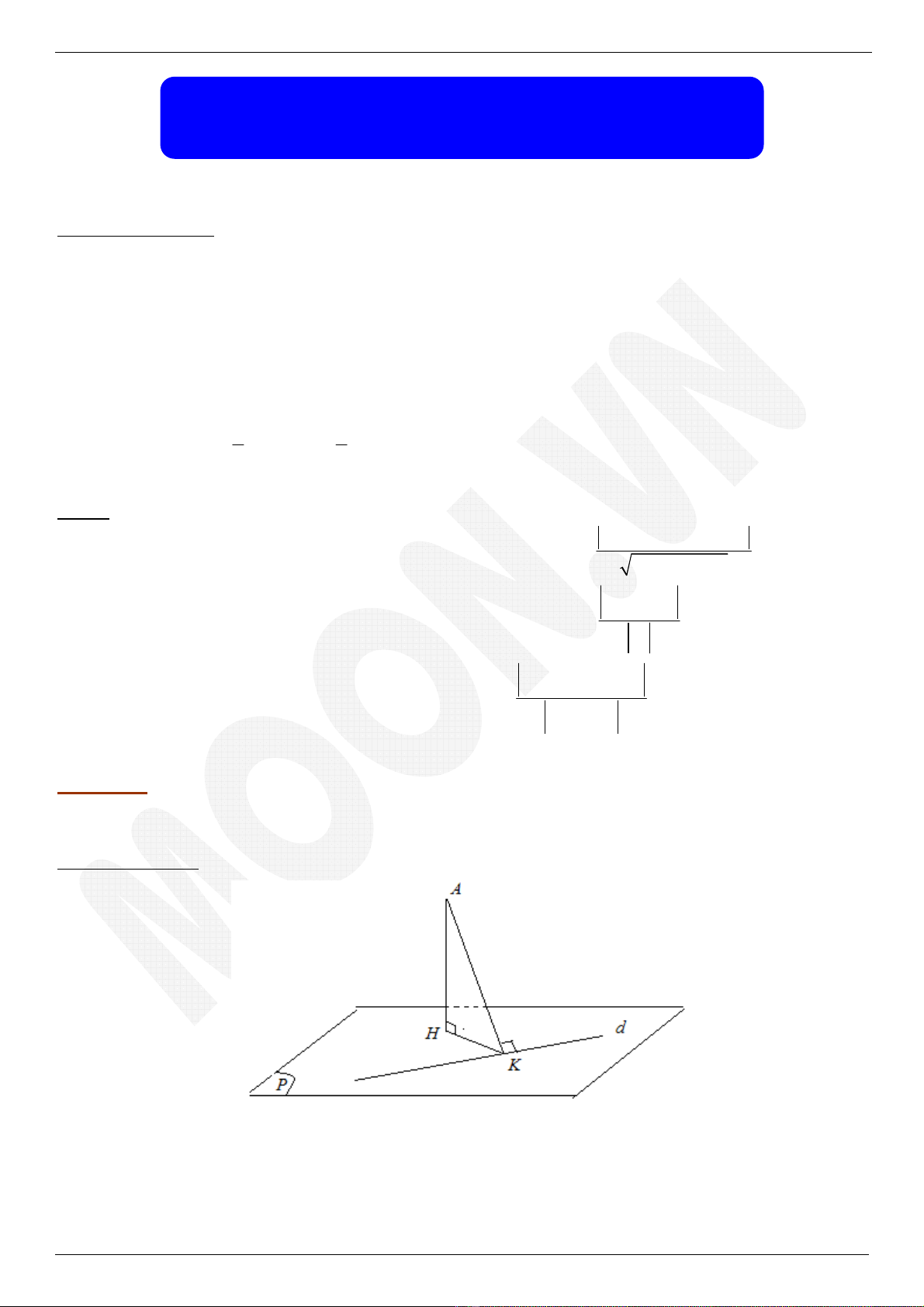
Bài toán 1: Lập phương trình mặt phẳng (P) chứa đường thẳng d sao cho khoảng cách từ A
đến (P) lớn nhất, với A là điểm không thuộc d
Phương pháp giải:
+) Kẻ
( ); ( ;( ))
⊥ ⊥ ⇒=
AH P AK d AH d A P
và điểm K cố định.
+) Ta có
(
)
max
;( )
≤⇒= ⇔ ≡
AH AK d A P AK H K
. Khi đó mặt phẳng (P) cần lập chứa đường thẳng d và
nhận véc tơ
AK
là véc tơ pháp tuyến.
14. CỰC TRỊ TRONG TỌA ĐỘ KHÔNG GIAN – P3
Thầy Đặng Việt Hùng
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com