Lecture 4: MẠCH TỔ HỢP
Biên soạn:Th.S Bùi Quốc Bảo
(Base on Floyd, Pearson Ed.)
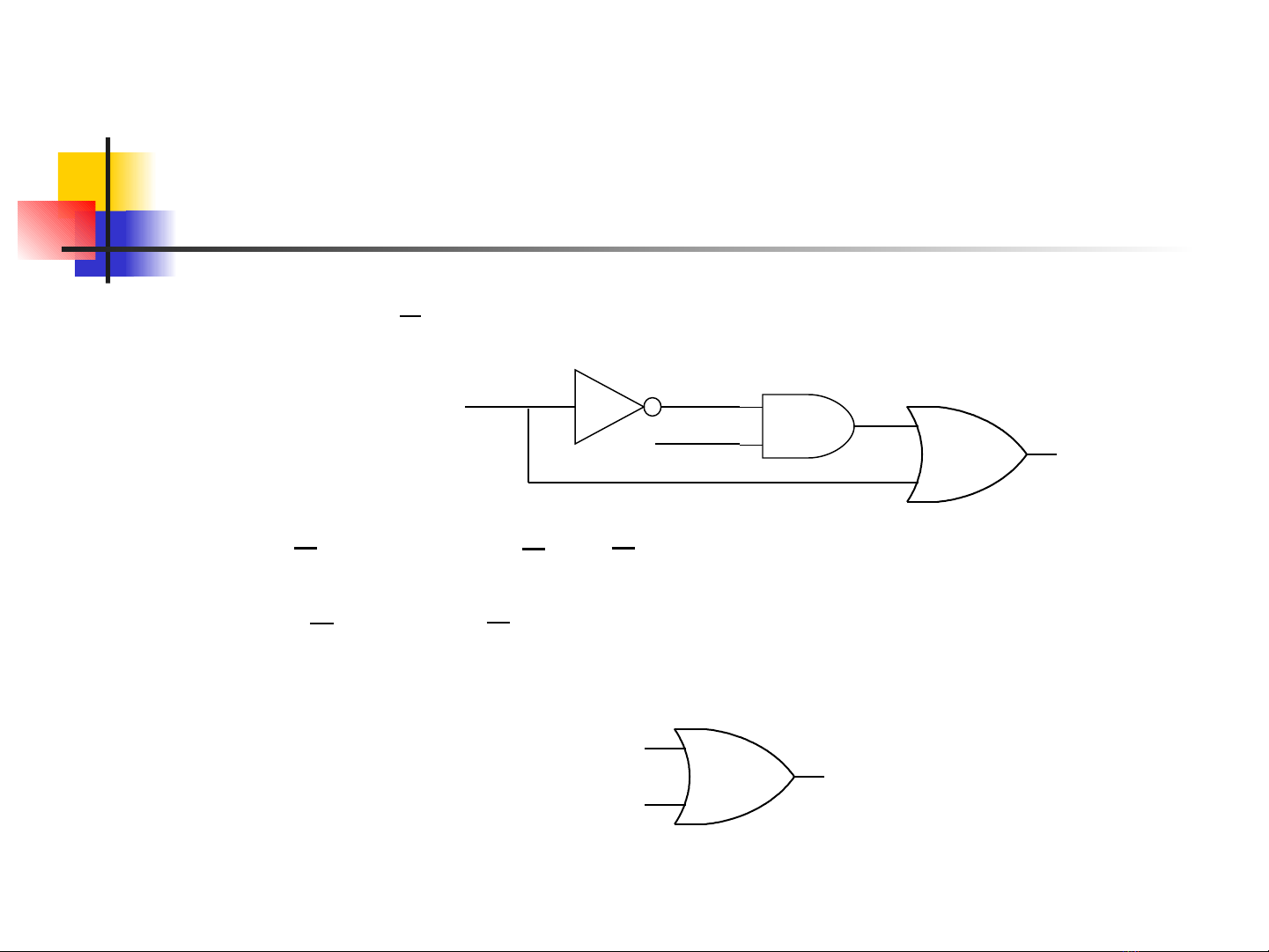
RÚT GỌN HÀM BOOLEAN
( , )F A B A AB
= +
A
BF
( )F A AB A B B AB
AB AB AB AB A B
= + = + +
= + + + = +
A
B
F
RÚT GỌN HÀM BOOLEAN
Hai hàm Boolean bằng nhau khi với
cùng ngõ vào chúng cho ngõ ra giống
nhau.
Khi thực hiện mạch, ta nên đưa hàm
Boolean về dạng tối ưu nhất
Điều đó giúp thực hiện hàm Boolean với
số cổng ít nhất, giảm chi phí thực hiện
và tăng tốc độ của mạch.
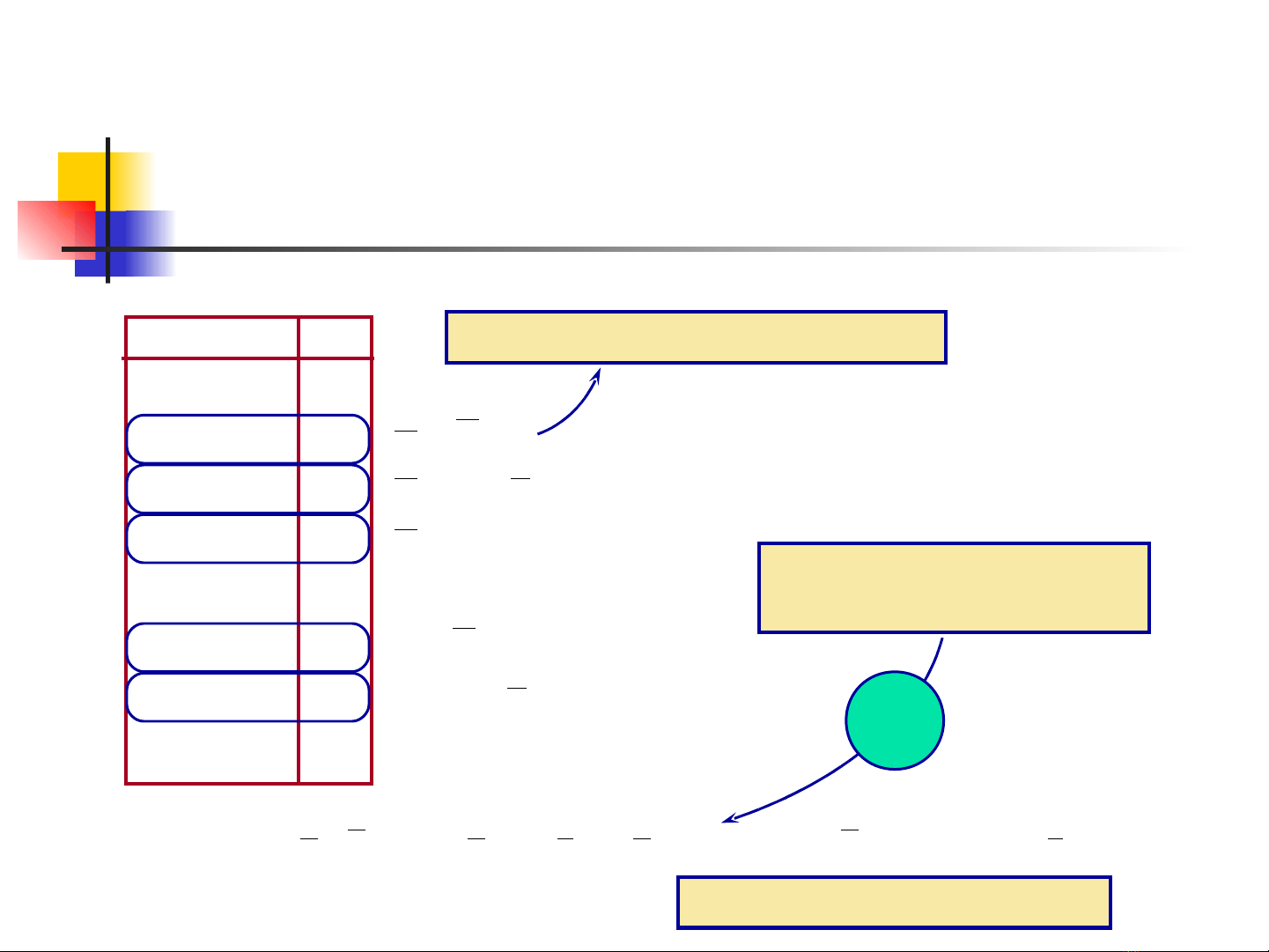
DẠNG CHÍNH TẮC SOP
a b c F
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
a b c
• •
a b c
• •
a b c
• •
a b c
• •
a b c
• •
Function F is true if any of
these and-terms are true!
Condition that a is 0, b is 0, c is 1.
OR
F a b c a b c a b c a b c a b c= • • + • • + • • + • • + • •( ) ( ) ( ) ( ) ( )
Sum-of-Products form (SOP)
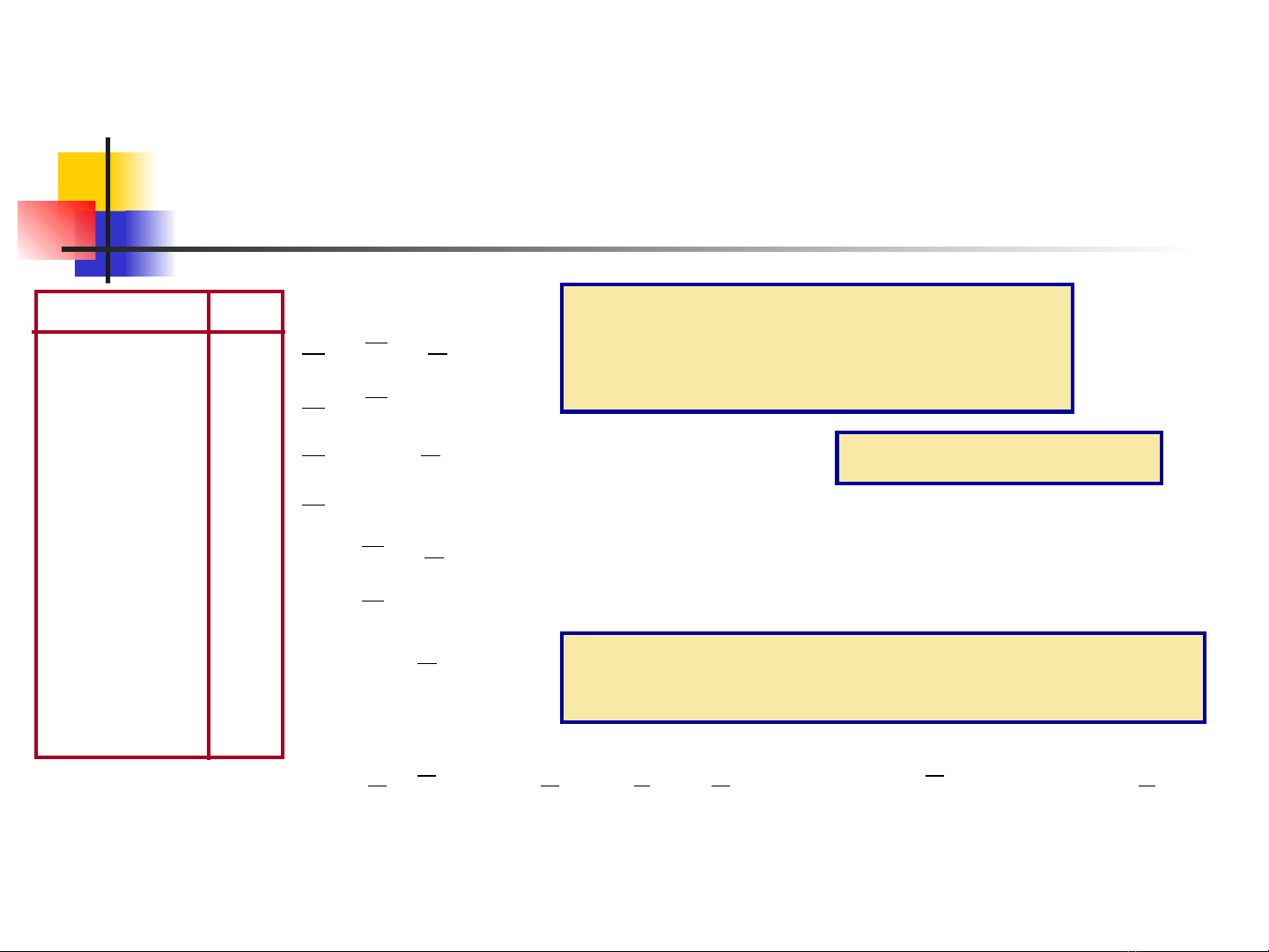
CÁC DẠNG CHÍNH TẮC
a b c
• •
a b c
• •
a b c
• •
a b c
• •
a b c
• •
a b c
• •
a b c
• •
a b c
• •
= m0
= m1
= m2
= m3
= m4
= m5
= m6
= m7
Note: Binary ordering
M t ộminterm là m t tích c a các ộ ủ
bi n ngõ vào, các bi n d ng ế ế ở ạ
bình th ng ho c là bù.ườ ặ
D ng chính t c 1 (SOP) g m các minterm ạ ắ ồ
OR l i v i nhauạ ớ
a b c F
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
F a b c a b c a b c a b c a b c
F
= • • + • • + • • + • • + • •
=
∑
( ) ( ) ( ) ( ) ( )
( , , , , )
m + m + m + m + m
F =
1 2 3 5 6
m
1 2 3 5 6